
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Зміст системи елементарних опорних сигналів
Процес пізнання, пов'язаний із засвоєнням нового прийому обчислень, може проводитись у двох напрямках: або розкривають його самі учні способом логічної роботи над виразом, або вони сприймають готовий запис обчислення виразу. І в одному, і в іншому випадках зусилля повинні бути спрямовані на те, щоб спеціальними прийомами полегшити учневі засвоєння обчислювального прийому: «Учити треба так, щоб знання здобувались за допомогою наявних уже знань, – у цьому, на мій погляд, полягає найвища майстерність дидакта» [15, с. 454].
Для сучасної дидактики провідним є положення про те, що «як би добре не було поставлене повідомлення учням готових знань пояснювально-ілюстративним методом, воно не забезпечить розвитку їх творчого мислення і пізнавальної самостійності» [15, с. 73].
Виконання того або іншого обчислення надалі вимагає відтворення і застосування певного прийому обчислення. Значну частину вправ на обчислення неможливо розв'язати без творчої діяльності учня, тобто без створення чогось власного,, оригінального, без активного напруження зусиль, поєднаних з діяльністю уяви і пам'яті; виявлення ініціативи. Розв'язування таких завдань вимагає активності розумової діяльності. Якщо учень при цьому ухиляється від розумових зусиль, то він не буде мати успіхів у виробленні вмінь і навичок навчальної діяльності взагалі й обчислювальних умінь і навичок зокрема.
«Якщо обмежитись засвоєнням обчислювальних прийомів в учнів і поясненням ходу розв'язування того чи іншого прикладу, як це рекомендується в традиційних методичних посібниках для учителів, то втрачаються можливості інтенсивної роботи над розвитком учнів: вони оволодівають окремими обчислювальними прийомами, не вникаючи в їх сутність. Справа зводиться в основному до заучування обчислювальних прийомів; дуже мало місця залишається для їх обдумування» [17, с. 119].
Критерієм для визначення методу роботи у відкритті способу обчислення є те, чи самі учні «відкрили» прийом обчислення виразу, чи він поданий учителем у готовому вигляді. Збіднений прийом обчислення, який засвоюється без необхідної думки й праці, неминуче призводить до лінивості думки. Недооцінка потенціальних можливостей розвитку дитини не менш шкідлива, ніж надмірне перевантаження її формування обчислювальних умінь і навичок необхідно будувати так, щоб додержуватись оптимального співвідношення між складністю і доступністю матеріалу, досягаючи потрібного ефекту.
Наведемо приклад застосування евристично-індуктивної бесіди під час ознайомлення учнів з обчислювальним прийомом додавання.
— Навчимося додавати одиницю до числа. Розв'яжемо приклад 1 + 5. Що показує число 1? (Яке число додається). Що показує число 5. (Скільки разів береться доданком число 1). Замініть приклад 1 + 5 сумою однакових доданків. (1 + 1 + 1 + 1 + 1 = 5). Запишіть. (1 + 5 = 1+1 + 1 + 1 + 1 + 1 = 5).
Але при ознайомленні з новим обчислювальним прийомом учителі надають перевагу методові пояснення або розповіді, вважаючи, що мистецтвом викладу володіють краще, ніж мистецтвом евристичної бесіди. Та забувають про те, що при застосуванні методу розповіді або пояснення учням доводиться більше засвоювати пам'яттю.
Ведуча роль у формуванні обчислювальних навичок належить учителеві. Вже на початкових етапах формування обчислювальних навичок учні І-ІV (І-ІІІ) класів можуть «відкривати» способи обчислень самостійно. Здійснюється це шляхом підвищення розумової активності учнів. Це можливе при такій організації пізнавальної самостійності молодших школярів, коли вони з самого початку усвідомлюють цілі і завдання уроку, самостійно здобувають знання не тільки в результаті виконання самостійних завдань, але й в процесі евристичної (індуктивної або дедуктивної) бесіди.
Ефективність формування обчислювальних навичок та вмінь школярів залежить від ряду факторів, першим із яких, і можна сказати визначальним є відокремлення певної та правильної орієнтованої основи дії.
Орієнтована основа дії (ООД) – це система елементарних операцій, які необхідно виконати для того, щоб дія досягла мети. У навчальному процесі ООД може бути подана у формі пам’ятки, в якій словесно описано алгоритми дій; блок-схеми, а також опорного сигналу – словесно-графічної схеми, з зазначенням взаємозв’язків елементарного змісту [14, с. 23-28].
Застосування пам’яток, опорних сигналів у процесі навчання дає змогу врахувати вікові особливості пізнавальних процесів у молодших школярів під час формування вмінь і навичок.
1. Додавання і віднімання числа 1
Опорний сигнал:
+ 1: наступне – 1: попереднє
 – це означає отримати
– це означає отримати  число.
число.
1. Інформативний – передає інформацію двома способами:
¾  символічним + 1: наступне
символічним + 1: наступне
 – 1: попереднє
– 1: попереднє
¾ мовним –  – це означає отримати
– це означає отримати  число.
число.
Таким чином враховані індивідуальні особливості дітей: одним достатньо для засвоєння символічного подання інформації, словесно сформулювати спосіб дії вони зможуть самостійно; іншим – треба ще й подати мовне формулювання, щоб вони мали можливість за необхідності звернутися до нього.
2. Компактний, наочний – для його сприйняття дитині не треба докладати додаткових зусиль, його можна збагнути «одним поглядом».
Такий опорний сигнал може бути попередньо заготовлений учителем.
Організація пошукової роботи з метою відокремлення ООД й оформлення опорного сигналу:
Завдання 1.
– Уважно розгляньте картку з розв’язками прикладів. Порівняйте ці приклади: чим вони схожі і чим відрізняються?
1, 2, 3, 4, 5, 6, 7, 8, 9, 10… 2 + 1 = 3
4 + 1 = 5
7 + 1 = 8
5 + 1 = 6
Перед виконанням цього завдання треба визначити місце кожного числа у натуральному ряді, яке є попереднє – наступним до даного; повторити назву компонентів при складанні:
Завдання 2.
– Перевірте на конкретних прикладах своє припущення: «до числа додати 1 – це означає отримати наступне число». Чи правильно вони розв’язані:
 3 + 1 = 4 1, 2, 3, 4, 5
3 + 1 = 4 1, 2, 3, 4, 5
 7 + 1 = 8 6, 7, 8, 9, 10
7 + 1 = 8 6, 7, 8, 9, 10
 2 + 1 = 3 1, 2, 3, 4, 5
2 + 1 = 3 1, 2, 3, 4, 5
Висновок: до числа 3 (7, 2) + 1 – це означає отримати наступне 4 (8, 3).
Завдання 3.
– Уважно розгляньте картку з розв’язаними прикладами. Порівняйте ці приклади: чим вони схожі і чим відрізняються?
1, 2, 3, 4, 5, 6, 7, 8, 9, 10…
2 – 1 = 1
4 – 1 = 3
7 – 1 = 6
5 – 1 = 4
Завдання 4.
– Перевірте на конкретних прикладах припущення: «Від числа відняти 1 – це означає отримати попереднє число».

 5 – 1 = 4 3, 4, 5, 6
5 – 1 = 4 3, 4, 5, 6
 9 – 1 = 8 7, 8, 9, 10
9 – 1 = 8 7, 8, 9, 10
2 – 1 = 1 1, 2, 3, 4
Висновок: від числа 5 (9, 2) відняти 1 – означає отримати попереднє число: 4 (8, 1).
Завдання 5.
– Уважно розгляньте, прочитайте опорний сигнал і складіть приклади додавання і віднімання 1.
На дошці вивішується картка з друкованою основою:
 + ; , , наступне
+ ; , , наступне
 то + = .
то + = .
– ; , , попереднє
то – = .
2. Додавання і віднімання числа 2:
Опорний сигнал:
2 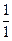
+ 2 : + 1 ; + 1 – 2 : – 1 ; – 1.
 – це означає
– це означає  1 і ще 1.
1 і ще 1.
3. Додавання і віднімання числа 3
Опорний сигнал:
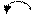
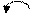
 3
3 
   + 1 + 1 + 1 + 1 + 1 + 1
|
  + 2 + 1 + 2 + 1
|
  + 1 + 2 + 1 + 2
|
  – 1 – 1 – 1 – 1 – 1 – 1
|
 – 1 – 2 – 1 – 2
|
| – 2 – 1 |
+ 3: – 3:
 можна кількома способами:
можна кількома способами:
1.  – 1 й ще 1, та й ще 1. 3.
– 1 й ще 1, та й ще 1. 3.  – 1 й ще 2.
– 1 й ще 2.
2.  – 2 й ще 1.
– 2 й ще 1.
4. Додавання та віднімання числа 4.
Опорний сигнал:
4 
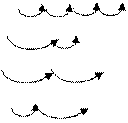 + 1 + 1 + 1 +1 + 1 + 1 + 1 +1
|
| + 3 + 1 |
| + 2 + 2 |
| + 1 + 3 |
| – 1 – 1 – 1 –1 |
| – 1 – 3 |
| – 2 – 2 |
| – 3 – 1 |
 + 4: – 4:
+ 4: – 4:
 можна кількома способами:
можна кількома способами:
1.  – 1 ще 1, та ще 1, та 1 3.
– 1 ще 1, та ще 1, та 1 3.  – 2 й ще 2.
– 2 й ще 2.
2.  – 3 та й 1. 4.
– 3 та й 1. 4.  – 1 й ще 3.
– 1 й ще 3.
5. Додавання та віднімання числа 5.
Опорний сигнал:
5 
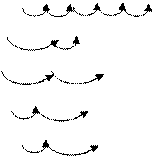 + 1 + 1 + 1 +1 + 1 + 1 + 1 + 1 +1 + 1
|
| + 4 + 1 |
| + 3 + 2 |
| + 2 + 3 |
| + 1 + 4 |
| – 1 – 1 – 1 –1 –1 |
| – 4 – 1 |
| – 3 – 2 |
| – 2 – 3 |
| – 1 – 4 |
 + 5: – 5:
+ 5: – 5:
 можна кількома способами:
можна кількома способами:
1.  – 1 й 1, 1 та 1, та й 1 3.
– 1 й 1, 1 та 1, та й 1 3.  – 3 й ще 2.
– 3 й ще 2.
2.  – 4 й ще1. 4.
– 4 й ще1. 4.  – 2 й ще 3.
– 2 й ще 3.
5.  – 1 і ще й 4.
– 1 і ще й 4.
Переставна властивість додавання.
Опорний сигнал:
€ € € ∆ ∆
3 + 2 = 5
∆ ∆ € € €
2 + 3 = 5
€ € € ∆ ∆ ∆ ∆ € € €
3 + 2 = 2 + 3
5 = 5
* Числа можна додати у будь-якому порядку. Від зміни місць доданків сума не змінюється.
Додавання чисел 6, 7, 8, 9.
Опорний сигнал:
 |

 6 6
6 6
€+ 7 7 +€
8 8
9 9
* Щоб додати 6, 7, 8, 9 – треба поміняти місцями доданки. Зручніше додати до більшого числа менше число.
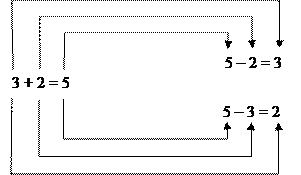
Взаємозв’язок додавання та віднімання.
Опорний сигнал:


€ € € ∆ ∆
3 + 2 = 5
€ € € ∆ ∆ ∆ ∆ € € €
5 – 2 = 3 5 – 3 = 2
 |
Віднімання числа 5.
Опорний сигнал:

 6 1/5
6 1/5
7 2/5
8 – 5 = 3/5 – 5 Наприклад:

 9 4/5 7 – 5 = 2 + 5 – 5 = 2
9 4/5 7 – 5 = 2 + 5 – 5 = 2
10 5/5 2 + 5
1. Віднімання числа 6.
Опорний сигнал:

 7 1/6
7 1/6
8 – 6 = 2/6 – 6
9 3/6
10 4/6



 9 – 6 = 3 + 6 – 6 = 3 10 – 6 = 4 + 6 – 6 = 4
9 – 6 = 3 + 6 – 6 = 3 10 – 6 = 4 + 6 – 6 = 4
3+6 4+6
Віднімання числа 7.
Опорний сигнал:

 8 1/7
8 1/7
9 – 7 = 2/7 – 7
10 3/7



 8 – 7 = 1 + 7 – 7 = 1 10 – 7 = 3 + 7 – 7 = 3
8 – 7 = 1 + 7 – 7 = 1 10 – 7 = 3 + 7 – 7 = 3
1+7 3+7
Віднімання числа 8.
Опорний сигнал:

 9 1/8
9 1/8
– 8 = – 8
10 2/8



 9 – 8 = 1 + 8 – 8 = 1 10 – 8 = 2 + 8 – 8 = 2
9 – 8 = 1 + 8 – 8 = 1 10 – 8 = 2 + 8 – 8 = 2
1+8 2+8
2. Віднімання числа 9.
Опорний сигнал:
10 – 9 = 1/9 – 9

 10 – 9 = 1 + 9 – 9 = 1
10 – 9 = 1 + 9 – 9 = 1
1+9
Віднімання чисел 6, 7, 8, 9 на підставі взаємозв’язку додавання і віднімання.
Пам’ятка:
1. Подаю зменшуване у вигляді суми двох доданків.
2. Якщо від суми відняти один з доданків, то залишиться другий доданок.
3. Записую (читаю) відповідь.
Читайте також:
- B. Тип, структура, зміст уроку і методика його проведення.
- I. Органи і системи, що забезпечують функцію виділення
- I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
- II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ І ВМІНЬ УЧНІВ
- II. Актуалізація опорних знань і вмінь учнів
- II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ І ВМІНЬ УЧНІВ
- II. Анатомічний склад лімфатичної системи
- III. Актуалізація опорних знань дітей та їхнього життєвого досвіду.
- III. Актуалізація опорних знань учнів.
- III. Актуалізація опорних знань.
- III. Актуалізація опорних знань.
- III. Актуалізація опорних знань.
| <== попередня сторінка | | | наступна сторінка ==> |
| | | Методика складання та вивчення таблиць додавання і віднімання |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |