Обчислення НСД і НСК способом канонічного розкладу на прості множники та за алгоритмом Евкліда.

Дільники і кратні. Спільні дільники і спільні кратні. Найбільший спільний дільник (НСД) і найменше спільне кратне (НСК), їх властивості.

6.Розглянемо два натуральних числа а та b. Якщо а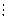b, то говорять, що а кратне b.

Означення: якщо а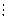b, то число а називається кратним до числа b.

Із означення відношення подільності відомо, що із а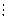bÛa=b·c. Якщо записати за допомогою характеристичної властивості множину чисел, кратних числу а, то будемо мати множину {a, 2a, 3a, … na…}. У множині чисел, кратних даному числу а є найменше число і немає найбільшого. За допомогою терміна “кратне” задається відношення подільності. Нехай задано множини чисел, кратних числу 3 і числу 5, тобто А={3,6,9,…3n,…} і B={5,10,15,…5n,…}. Утворимо перетин цих множин AÇB={15,30,45,…15n,…}. Множина AÇB задає нам спільні кратні чисел 3 і 5.

Означення: Будь-яке число, кратне числам а₁, а_2, а₃,…,а_n називається спільним кратним цих чисел.

Означення: найменше із спільних кратних чисел а₁, а_2,а₃,…а_k називається найменшим спільним кратним цих чисел.

Найменше спільне кратне прийнято позначати так: НСК(а₁, а₂, а₃,…а_k) або К(а₁, а_2,а₃,…а_k). Розглянемо властивості НСК, сформулювавши відповідні теореми для випадку двох чисел.

Властивість 1: кожне спільне кратне даних чисел ділиться на їх найменше спільне кратне.

Доведення: для спрощення викладок доведення теореми проведемо для випадку двох чисел. Нехай НСК(a,b)=k і CK(a,b)=d. Доведемо, що d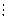k. Доведення проведемо методом від супротивного, припустивши, що 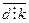, тобто, згідно означення операції ділення з остачею виконуються умови: d=kq+r і 0£r<k. Звідси r=d-kq. Оскільки d є спільним кратним (СК) чисел a і b, то . Оскільки k=НСК(a,b), то . Оскільки r<k, a£ k, то r – ділиться на число, більше, ніж воно саме, тобто число r є спільним кратним чисел a і b. Отже, СК(a,b)=r. А це можливо тоді, коли d–k·q=0, r=0, а це суперечить припущенню, що 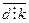. Отже, припущення хибне і теорема доведена.

Властивість 2: якщо НСК(a,b)=k, то для будь-якого сÎN НСК(ac,bc)=ck.

Ця теорема говорить, що будь-який спільний множник можна виносити за знак НСК. Ввівши в попередніх пунктах означення дільника даного числа, ми з’ясували, що кількість дільників є завжди скінченною, найменшим дільником будь-якого числа є 1, а відношення „число b є дільником числа а” є оберненим до відношення „число а кратне числу b”.

Означення: всяке число, на яке ділиться кожне із чисел а₁, а₂, а₃…а_к називається спільним дільником цих чисел.

Означення найбільший із спільних дільників чисел а₁,а₂,а₃…а_к називається найбільшим спільним дільником чисел а₁, а₂, а₃…а_к і позначається НСД(а₁,а₂,а₃…а_к) або Д(а₁,а₂,а₃…а_к).

Означення: числа а₁, а₂, а₃…а_к називаються взаємно простими, якщо їх найбільший спільний дільник дорівнює 1. .

Властивість 1: якщо 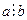, то НСК(a,b)=a, а НСД(a,b)=b.

Доведення: за умовою 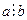і 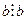, тобто СД(a,b)=b, оскільки a>b, то НСД(a,b)=b. За умовою , то число а є спільним кратним для чисел a і b. Оскільки a>b, то а=НСК(а, b). Теорема доведена.

Властивість 2: будь-який спільний дільник даних чисел є дільником їх спільного дільника.

Властивість 3: спільні дільники даних чисел можна виносити, як за знак найменшого спільного кратного, так і за знак найбільшого спільного дільника.

Властивість 4: найменше спільне кратне даних чисел дорівнює добутку цих чисел, поділеному на найбільший спільний дільник цих чисел, тобто: .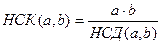

Справедливість властивостей 2-4 приймемо без доведення.

7. У теорії чисел для знаходження НСК і НСД використовують два способи:

1) спосіб розкладу чисел на прості множники. Для знаходження НСД цим способом, який називають способом канонічного розкладу, потрібно розкласти дані числа в добуток простих множників і для знаходження НСД потрібно записати добуток спільних множників у найменшому степені. Для знаходження НСК даних чисел потрібно розкласти ці числа на прості множники, а потім записати добуток всіх простих множників у найбільшому степені.

2) спосіб знаходження НСД, який називають алгоритмом Евкліда. Він ґрунтується на такій теоремі.

Теорема: якщо натуральне число а можна представити у вигляді a=b·q+r, де a,b,q,rєN, то множина спільних дільників чисел a і b співпадає з множиною спільних дільників чисел b і r.

Доведення: нехай a=b·q+r. Позначимо через М множину таких натуральних чисел d, які є дільниками чисел а і b, тобто М={dÎN/a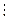dÙb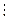d}. Через К позначимо множину таких натуральних чисел k, які є дільниками чисел b і r, тобто K={kÎN/b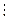kÙr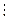k}. Для доведення теореми нам потрібно показати, що кожен елемент множини M є елементом множини K і навпаки. Отже, доведення складається із двох частин.

У першій частині доведемо, що кожен елемент множини M є елементом множини K. Нехай xÎM. Оскільки (a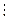x)Ù(b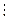x), то за теоремою про подільність різниці та добутку (a-bq)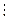x. Зважаючи на те, що a-bq=r, маємо r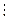x. Тоді 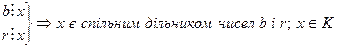. Оскільки елемент х в множині M ми вибирали довільно, то наші міркування можна повторити для кожного елемента множини M, а тому кожен елемент множини M є елементом множини K, тобто MÌK. Перша частина теореми доведена.

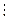У другій частині доведемо, що кожен елемент множини K є елементом множини M. Нехай ). Оскільки b·q+r=a, то ау. Отже, 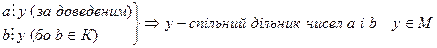. Оскільки елемент y ми вибираємо довільно, то наші міркування можна повторити для кожного елемента множини K. Отже, KÌM. Друга частина теореми доведена.

За доведеним у першій частині MÌK, а за доведеним у другій частині KÌM. Відповідно до означення рівності множин випливає, що M=K, тобто множини співпадають. Теорема доведена повністю.

Ця теорема дає можливість звести знаходження НСД для чисел a і b до знаходження НСД чисел b і r, які менші за задані числа. Теоретичною основою цього є наступна теорема.

Теорема: в алгоритмі Евкліда, який застосований до натуральних чисел a і b, остання, відмінна від нуля остача, буде дорівнювати НСД цих чисел.

Доведення: для того, щоб знайти НСД даних чисел за алгоритмом Евкліда треба найбільше число поділити на найменше, потім найменше число на остачу, потім першу остачу на другу і т.д., аж доки не отримаємо в остачі 0. Тоді остання відмінна від 0 остача і буде НСД. Якщо a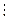b, то НСД(а,b)=b. Якщо ж а не ділиться націло на b, то відповідно до теореми про ділення з остачею маємо: a=bq+r, де a,b,q,rÎN, a>b>r>r₁>r₂>…>r_k і b=rq₁+r₁, r=r₁q₂+r₂ тощо. Оскільки ми маємо a>b>r>r₁>r₂>…>r_k, то за принципом найменшого числа ми прийдемо до випадку, коли якесь r_k=0, а тому ділення буде виконуватися націло. Тоді НСД(r_k-1,0)=r_k-1. Теорема доведена.

Проілюструємо обидва способи знаходження НСД і НСК на таких прикладах.

Вправа 1: знайти НСД(248, 1024) за допомогою канонічного розкладу.

Розв’язання:

Розкладаємо числа 248 і 1024 на прості множники (див. таблицю № 4.9.).






248=2³·31





1024=2¹⁰

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Основна теорема арифметики цілих невід’ємних чисел.	\|	Ознаки подільності на складені числа.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.