• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Вимірний арифметичний простір

Алгебри

Тема: Векторні простори.

Лекція 5

План лекції:

1. 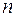-вимірний арифметичний простір.

2. Поняття, приклади і найпростіші властивості векторного простору.

3. Лінійна залежність системи векторів. Базис і розмірність векторного простору.

4. Координати вектора у векторному просторі. Розкладання вектора за базисом.

5. Підпростори векторного простору.

6. Лінійний оператор і його матриця

7. Поняття алгебри. Приклади алгебр.

8. Ізоморфізм та гомоморфізм алгебр.

Нехай 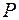– деяке числове поле. Числа з 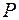будемо позначати малими латинськими буквами.

Означення. Будь-який впорядкований набір з 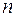чисел 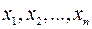з поля 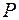називається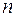-вимірним числовим вектором. Числа 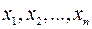називаються координатами або компонентами вектора. Позначається .

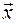Компоненти вектора розташовують в рядок:

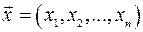
або в стовпчик

.

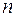-вимірний вектор, всі компоненти якого дорівнюють нулю, називається нульовим або нуль-вектором: .

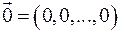Означення. Два числових вектори 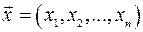та 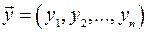рівні тоді і тільки тоді, коли рівні їх відповідні компоненти:

.

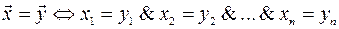Відзначимо, що два числових вектори не можуть бути рівні, якщо число компонент в них неоднакове.

Позначимо через 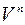множину всіх 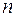-вимірних числових векторів з компонентами з 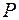. Визначимо в цій множині операції додавання векторів і множення вектора на число з поля .

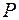Означення. Сумою векторів 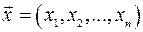та 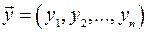називається вектор

.

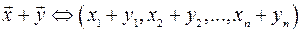Означення. Добутком вектора 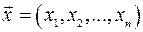на число 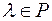називається вектор

.

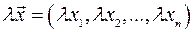Неважко переконатися в тому, що множина 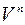всіх 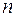-вимірних числових векторів є абелевою групою відносно додавання. Дійсно, оскільки операція додавання 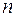-вимірних числових векторів зводиться до додавання їх відповідних координат, то вона асоціативна:

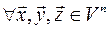
1. 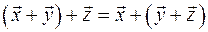– асоціативність додавання;

і комутативна:

2. 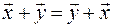– комутативність додавання;

в множині 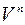міститься нульовий елемент, ним є нуль-вектор :

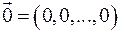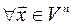
3. 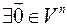: 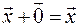– існування нульового елемента ;

для кожного 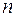-вимірного числового вектора в множині 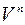міститься протилежний йому вектор :

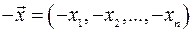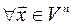
4. 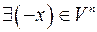: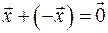– існування протилежного елемента;

З означення добутку вектора 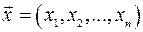на число 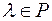випливає, що операція множення вектора на число асоціативна:

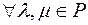
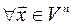
5. 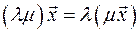– асоціативність множення на число;

6. .

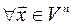
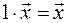Крім того, мають місце

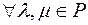
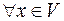
7. 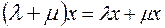– дистрибутивність множення на число відносно додавання чисел ;

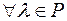
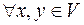
8. 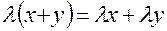– дистрибутивність множення на число відносно додавання елементів.

Означення. Множина 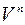всіх 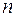-вимірних числових векторів з компонентами з поля 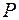разом з введеними операціями додавання векторів і множення вектора на число з поля 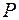, для яких виконуються всі властивості лінійних дій над векторами, називається 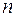-вимірним арифметичним простором над полем .

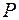Читайте також:

1. Арифметичний цикл ДЛЯ
2. Внутрішній простір будівель
3. Входження України в європейський простір вищої освіти
4. Забезпечення поступового входження національної економічної системи у світову економіку, у глобальний економічний простір.
5. Звукова потужність джерела W, Вт визначається загальною кількістю звукової енергії, яка випромінюється джерелом шуму в навколишній простір за одиницю часу
6. Інтегрування господарства економіки України до у світовий економічний простір
7. Інформаційний простір в умовах соціально-економічної трансформації українського суспільства.
8. Колір і простір в дизайні інтер'єру
9. Культурний простір як простір смислових опозицій
10. Матерія та рух. Простір і час. Методологічне значення проблеми матерії та руху для біології та медицини.
11. Монтажний час і простір

Переглядів: 1702