
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Системи та сукупності рівнянь з двома змінними та способи (алгебраїчні та графічні) їх розв’язування.
4. Нехай дано два рівняння з двома змінними 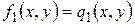 і
і  . Говорять, що вони утворюють систему рівнянь з двома змінними, якщо потрібно знайти всі пари чисел, при підстановці яких в кожне рівняння системи воно перетворюється в правильну числову рівність. Якщо потрібно знайти всі пари чисел, при підстановці яких хоча б в одне рівняння воно перетворюється в правильну числову рівність, то говорять про сукупність двох рівнянь з двома невідомими. Таким чином, приймемо наступні означення.
. Говорять, що вони утворюють систему рівнянь з двома змінними, якщо потрібно знайти всі пари чисел, при підстановці яких в кожне рівняння системи воно перетворюється в правильну числову рівність. Якщо потрібно знайти всі пари чисел, при підстановці яких хоча б в одне рівняння воно перетворюється в правильну числову рівність, то говорять про сукупність двох рівнянь з двома невідомими. Таким чином, приймемо наступні означення.
Означення: системою двох рівнянь з двома невідомими називається кон’юнкція двох рівнянь з двома змінними.
Означення: сукупністю двох рівнянь з двома невідомими називається диз’юнкція двох рівнянь з двома змінними.
Систему двох рівнянь з двома невідомими, яка складається із рівнянь 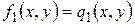 і
і  символічно позначають так:
символічно позначають так:  або
або 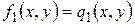 Ù
Ù (І). Сукупність двох рівнянь з двома невідомими, яка складається із рівнянь f1(х;у)=g1(х;у) і f2(х;у)=g2(х;у) символічно позначають так: f1(х;у)=g1(х;у)Úf2(х;у)=g2(х;у) або
(І). Сукупність двох рівнянь з двома невідомими, яка складається із рівнянь f1(х;у)=g1(х;у) і f2(х;у)=g2(х;у) символічно позначають так: f1(х;у)=g1(х;у)Úf2(х;у)=g2(х;у) або
 f1(х;у)=g1(х;у)
f1(х;у)=g1(х;у)
f2(х;у)=g2(х;у). (ІІ).
Означення:пара чисел 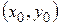 , при підстановці яких в кожне рівняння системи замість змінних
, при підстановці яких в кожне рівняння системи замість змінних 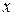 і
і  , ми одержуємо правильні числові рівності називається розв’язком системи (І).
, ми одержуємо правильні числові рівності називається розв’язком системи (І).
Означення:пара чисел 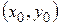 , при підстановці яких хоча б в одне рівняння сукупності замість змінних
, при підстановці яких хоча б в одне рівняння сукупності замість змінних 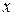 і
і  , ми одержуємо правильну числову рівність називається розв’язком сукупності (ІІ).
, ми одержуємо правильну числову рівність називається розв’язком сукупності (ІІ).
Множину всіх таких пар 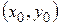 називають множиною розв’язків відповідно даної системи чи даної сукупності. Як видно, множина розв’язків системи є перетином множин розв’язків обох рівнянь системи, а множина розв’язків сукупності є об’єднанням множин розв’язків обох рівнянь сукупності. Система рівнянь являє собою кон’юнкцію цих рівнянь, бо система рівнянь буде мати розв’язки тоді, коли існує така пара чисел, що обидва рівняння перетворюються в правильні числові рівності. Саме тому ми систему рівнянь записуємо і так:
називають множиною розв’язків відповідно даної системи чи даної сукупності. Як видно, множина розв’язків системи є перетином множин розв’язків обох рівнянь системи, а множина розв’язків сукупності є об’єднанням множин розв’язків обох рівнянь сукупності. Система рівнянь являє собою кон’юнкцію цих рівнянь, бо система рівнянь буде мати розв’язки тоді, коли існує така пара чисел, що обидва рівняння перетворюються в правильні числові рівності. Саме тому ми систему рівнянь записуємо і так:  . Для того, щоб це показати, потрібно довести, що всі розв’язки системи перетворюють кон’юнкцію двох предикатів в істинне висловлення, і навпаки, всі значення при яких кон’юнкція предикатів істинна, перетворюють кожен із них в правильне висловлення, тобто в правильну числову рівність. Нехай пара чисел
. Для того, щоб це показати, потрібно довести, що всі розв’язки системи перетворюють кон’юнкцію двох предикатів в істинне висловлення, і навпаки, всі значення при яких кон’юнкція предикатів істинна, перетворюють кожен із них в правильне висловлення, тобто в правильну числову рівність. Нехай пара чисел 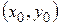 є розв’язком системи. Тоді при підстановці чисел
є розв’язком системи. Тоді при підстановці чисел 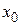 і
і 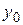 замість
замість 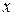 і
і  ми будемо мати дві істинні числові рівності, тобто кон’юнкція f1(х0;у0)=g1(х0;у0)Ù f2(х0;у0)=g2(х0;у0) буде істинною. Навпаки, якщо із двох рівнянь з двома змінними утворено кон’юнкцію і при підстановці пари чисел
ми будемо мати дві істинні числові рівності, тобто кон’юнкція f1(х0;у0)=g1(х0;у0)Ù f2(х0;у0)=g2(х0;у0) буде істинною. Навпаки, якщо із двох рівнянь з двома змінними утворено кон’юнкцію і при підстановці пари чисел 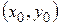 вона істинна, то істинні обидва рівняння, а отже пара чисел
вона істинна, то істинні обидва рівняння, а отже пара чисел 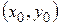 є розв’язком системи
є розв’язком системи  .
.
Сукупність рівнянь являє собою диз’юнкцію цих рівнянь, бо сукупність рівнянь буде мати розв’язки тоді, коли існує така пара чисел, що хоча б одне рівняння перетворюються в правильну числову рівність. Саме тому ми сукупність рівнянь записуємо і так: f1(х;у)=g1(х;у)Úf2(х;у)=g2(х;у). Для того, щоб це показати, потрібно довести, що всі розв’язки сукупності перетворюють диз’юнкцію двох предикатів в істинне висловлення, і навпаки, всі значення, при яких диз’юнкція предикатів істинна, перетворюють хоча б одне із них в правильне висловлення, тобто в правильну числову рівність. Нехай пара чисел 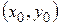 є розв’язком сукупності. Тоді при підстановці чисел
є розв’язком сукупності. Тоді при підстановці чисел 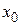 і
і 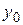 замість
замість 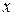 і
і  ми будемо мати принаймні одну істинну числову рівність, тобто диз’юнкція f1(х0;у0)=g1(х0;у0)Úf2(х0;у0)=g2(х0;у0) буде істинною. Навпаки, якщо із двох рівнянь з двома змінними утворено диз’юнкцію і при підстановці пари чисел
ми будемо мати принаймні одну істинну числову рівність, тобто диз’юнкція f1(х0;у0)=g1(х0;у0)Úf2(х0;у0)=g2(х0;у0) буде істинною. Навпаки, якщо із двох рівнянь з двома змінними утворено диз’юнкцію і при підстановці пари чисел 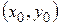 вона істинна, то принаймні одне рівняння перетвориться в істинну числову рівність, а отже пара чисел
вона істинна, то принаймні одне рівняння перетвориться в істинну числову рівність, а отже пара чисел 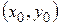 є розв’язком сукупності (ІІ).
є розв’язком сукупності (ІІ).
Означення:розв’язати систему рівнянь – це означає знайти множину її розв’язків.
Означення:розв’язати сукупність рівнянь – це означає знайти множину її розв’язків.
Означення: дві системи рівнянь називаються рівносильними, якщо вони визначені на одній множні та всі розв’язки однієї системи рівнянь є розв’язками другої і навпаки.
Означення: дві сукупності рівнянь називаються рівносильними, якщо вони визначені на одній множині та всі розв’язки однієї сукупності рівнянь є розв’язками другої і навпаки.
Дві системи чи сукупності рівнянь можуть бути рівносильними в одній числовій області і нерівносильними в іншій. До алгебраїчних методів розв’язування систем рівнянь відносять такі методи:
а) метод підстановки. Суть цього методу полягає в тому, що одне із рівнянь системи замінюють рівносильним йому рівнянням, але таким, в якому визначене одне із невідомих, і підставляють у друге рівняння. Внаслідок такої підстановки друге рівняння стає рівнянням з однією змінною.
Вправа: розв’язати систему рівнянь: х-2у=3Ù3х-5у=7.
Читайте також:
- I. Органи і системи, що забезпечують функцію виділення
- I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
- II. Анатомічний склад лімфатичної системи
- IV. Розподіл нервової системи
- IV. Система зв’язків всередині центральної нервової системи
- IV. Філогенез кровоносної системи
- POS-системи
- VI. Філогенез нервової системи
- Автокореляційна характеристика системи
- АВТОМАТИЗОВАНІ СИСТЕМИ ДИСПЕТЧЕРСЬКОГО УПРАВЛІННЯ
- АВТОМАТИЗОВАНІ СИСТЕМИ УПРАВЛІННЯ ДОРОЖНІМ РУХОМ
- Автоматизовані форми та системи обліку.
| <== попередня сторінка | | | наступна сторінка ==> |
| Малюнок № 6.4. | | | Розв’язання. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |