
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Перетворення координат Лоренца
В класичній механіці Ньютона для тіл, які рухаються з швидкостями, набагато меншими за швидкість світла (v<<с), виконується механічний принцип відносності Галілея.
Суть класичного принципу відносності полягає в тому, що закони динаміки однакові для всіх інерціальних систем відліку.
Розглянемо дві інерціальні системи координат відліку (рис.5.1).
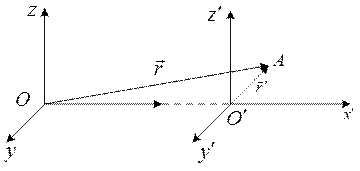
Рис. 5.1.
Інерціальну систему з координатами x, y, z будемо вважати нерухомою. Система, координати якої 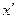 ,
,  ,
, 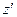 рухається відносно нерухомої системи з сталою швидкістю u.
рухається відносно нерухомої системи з сталою швидкістю u.
В довільний момент часу t
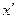 = x - ut,
= x - ut,  =y,
=y, 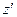 =z,
=z,  = t. (5.1.1)
= t. (5.1.1)
Ці перетворення координат називаються перетвореннями Галілея.
Диференціюємо ці перетворення за часом і знайдемо закон складання швидкостей у класичній механіці:

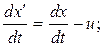
 . (5.1.2)
. (5.1.2)
де 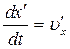 - швидкість руху матеріальної точки в напрямі осі x відносно штрихованої системи координат;
- швидкість руху матеріальної точки в напрямі осі x відносно штрихованої системи координат;  - швидкість руху матеріальної точки в напрямі осі х відносно нерухомої системи координат; u – швидкість руху штрихованої системи відносно не штрихованої системи.
- швидкість руху матеріальної точки в напрямі осі х відносно нерухомої системи координат; u – швидкість руху штрихованої системи відносно не штрихованої системи.
У векторній формі класичний закон складання швидкостей матиме вигляд:
 . (5.1.3)
. (5.1.3)
Диференціюємо за часом вираз (5.1.3), одержимо:
 , або
, або  . (5.1.4)
. (5.1.4)
Прискорення матеріальної точки інваріантне відносно перетворень координат Галілея. Можна також стверджувати, що сили теж є інваріантними величинами відносно перетворень координат Галілея
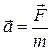 . (5.1.5)
. (5.1.5)
Висновок: У будь-яких інерційних системах відліку всі механічні явища за однакових умов є інваріантні (однакові).
Цей висновок носить назву механічного принципу відносності.
У 1905 році видатний фізик ХХ сторіччя Альберт Ейнштейн, аналізуючи великий експериментальний матеріал, сформулював два постулати створеної ним спеціальної теорії відносності, суть яких така:
- у будь-яких інерційних системах відліку всі фізичні явища за однакових умов відбуваються однаково;
- швидкість світла у вакуумі не залежить від швидкості руху джерела світла.
З першого постулату Ейнштейна виходить, що за допомогою будь-яких фізичних дослідів, поставлених у замкнутій системі, неможливо виявити рухається ця система чи перебуває у стані спокою.
Другий постулат Ейнштейна суперечить класичному закону додавання швидкостей.
З постулатами спеціальної теорії відносності перебувають у відповідності не перетворення координат Галілея, а дещо складніші перетворення, які називаються перетвореннями координат Лоренца.
Нехай штрихована система рухається відносно не штрихованої системи координат з сталою швидкістю u, при чому u»c. Нехай швидкість u направлена уздовж осі ОХ. Тоді релятивістські перетворення координат Лоренца будуть мати вигляд:
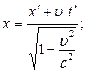
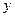 =
=  ;
;  =
= 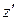 ;
;  . (5.1.6)
. (5.1.6)
Координати штрихованої системи по відношенню до координат нештрихованої системи:
 ;
; 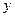 =
=  ;
;  =
= 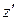 ;
; 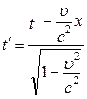 . (5.1.7)
. (5.1.7)
У випадку, коли v<<c, перетворення координат Лоренца переходять у класичні перетворення Галілея:
х=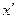 + ut,
+ ut, 
 ,
,  ,
,  ;
;
або
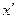 =x -u t,
=x -u t, 
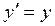 ,
, 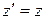 ,
,  . (5.1.8)
. (5.1.8)
Класична механіка придатна для розгляду таких рухів, швидкості яких, порівняно з швидкістю світла, досить малі.
Механіка, яка розглядає рух тіл з швидкостями, близькими до швидкості світла, називається релятивістською механікою.
5.2. Наслідки перетворення координат Лоренца.
Читайте також:
- Адаптивні хвилькові перетворення : Хвилькові пакети.
- Вантажообіг і координати магазинів, які обслуговуються
- Визначення перетворення за Лапласом
- Визначення скалярного добутку через координати.
- Визначення. Матриці, отримані в результаті елементарного перетворення, називаються еквівалентними.
- Визначте соціальні перетворення в процесі радянізації українського суспільства.
- Виконаємо лінійне перетворення
- Вимірювальні сигнали, перетворення вимірювальних сигналів, форми вимірювальної інформації
- Вираження мішаного добутку через координати векторів.
- Вирішення проблеми не міститься в існуючому знанні та не може бути отримане шляхом перетворення наявної наукової інформації.
- Вирішення проблеми не міститься в існуючому знанні та не може бути отримане шляхом перетворення наявної наукової інформації.
- Властивості зворотного перетворення за Лапласом
| <== попередня сторінка | | | наступна сторінка ==> |
| Теорема Штейнера | | | Закон складання швидкостей |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |