
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Лекція № 1. ДИСКРЕТНЕ І БЕЗПЕРЕРВНЕ
1.1. Вступ|вступ|
Дискретна математика – це математика, не пов'язана з поняттями нескінченності, межі і безперервності. Термін «дискретна математика» еквівалентний терміну «кінцева|скінченна| математика». Дискретна математика має широкий спектр використовування|застосувань|, перш за все|передусім| в областях, пов'язаних з інформаційними технологіями і комп'ютерами. Коли говорять «цифрова обчислювальна машина», те слово «цифрова» указує|вказує| на принципово дискретний характер|вдачу| роботи даного пристрою|устрою|.
Хоча відмінність між дискретним і безперервним інтуїтивно зрозуміло, все-таки воно достатньо|досить| тонко. Щоб правильно зрозуміти його сенс|зміст,рацію| і уникнути непорозумінь|нерозумінь|, необхідно ознайомитися з|із| основами теорії множин|безлічі|.
1.2. Рахункові і незліченні числові множини|безліч|
Теорія множин|безлічі| з'явилася|появилася| в кінці 19 століття завдяки роботам німецького математика Георга Кантора (1845-1918). Поняття множини|безлічі| належить до фундаментальних невизначуваних понять математики. Можна сказати, що множина|безліч| – це будь-яка сукупність об'єктів. Приклади|зразки| множин|безлічі|: безліч будинків|домів,хат| в місті, безліч його жителів|мешканців|, безліч зірок на небі|піднебінні| і т.д.
Серед інших множин|безлічі| особливе положення|становище| займають|позичають,посідають| так звані числові множини|безліч|. Перша числова множина|безліч|, яка відкрилася|відчинилася| людській свідомості, була безліч натуральних чисел (позначається|значиться| буквою|літерою| N): 1, 2, 3, … Ідею їх існування підказувала сама природа (Nature). «Три дерева, три апельсина, три людини» – натуральне число «три» якось зв'язували ці різні об'єкти, додавали|наділяли,надавали| їм якусь|деяку| спільність.
Але|та| навіть прості натуральні числа мали якусь таємницю. Ця множина|безліч| мала початок (число 1), проте|однак| не мало кінця. Яким би великим не було б натуральне число, можна було б одержати|отримати| ще більше, додавши до нього одиницю. Таким чином, безліч натуральних чисел – нескінченна|безконечна| множина|безліч|.
Існують рахункові і незліченні числові множини|безліч|. Очевидно, що множина|безліч|, складена з|із| кінцевого|скінченного| числа натуральних чисел, буде рахунковою. Проте|однак| бувають і нескінченні|безконечні| рахункові множини|безліч|. Якщо елементам нескінченної|безконечної| множини|безлічі| можна поставити у взаємно однозначну відповідністьчисла натурального ряду|лави,низки|, то така множина|безліч| називається рахунковою.
Наприклад, безліч парних чисел рахункова. Числу 2 можна поставити у відповідність число 1, числу 4 – 2, числу 6 – 3 і т.д. Цей процес можна продовжувати до безкінечності.
Очевидно, що рахункова і безліч натуральних чисел, кратних трьом (або чотирьом, або п'яти.). Нескінченні|безконечні| множини|безліч|, що задовольняють умові взаємно однозначної відповідності, називаються рівнопотужними.
Таким чином, безліч парних чисел і натуральних чисел рівнопотужні|, хоча інтуїція начебто|неначебто,неначе| підказує, що перша множина|безліч| «менша» за другу. Одна з основних новаторський ідей Кантора полягає в тому, що співвідношення, справедливі для кінцевих|скінченних| множин|безлічі|, не застосовні до нескінченних|безконечних|.
Стародавні|древні| індуси «винайшли» число нуль, а також негативні|заперечні| цілі числа. Разом з натуральними числами ці числа складають безліч цілих чисел (позначається|значиться| латинською буквою|літерою| Z). Натуральні числа і нуль утворюють безліч цілих ненегативних чисел (позначається|значиться|  ).
).
Ці множини|безліч| також є|з'являються,являються| рахунковими, оскільки|тому що| можна встановити взаємно однозначну відповідність між ними і безліччю натуральних чисел, як показано табл. 1.1.
Таблиця 1.1
| N | |||||||
| Z | – 3 | – 2 | – 1 |
Продовжуючи освоювати нові абстрактні поняття, люди ввели|запровадили| в ужиток|побут| дробові числа, які одержують|отримують| шляхом ділення|поділки,розподілу,поділу| одного цілого числа на інше. Такі числа називаються раціональними, оскільки метод їх отримання|здобуття| цілком|сповна| доступний розумінню (безліч раціональних чисел позначається|значиться| буквою|літерою| Q).
Кантор відкрив|відчинив|, що безліч раціональних чисел також рахункова, хоча усюди|всюди| щільно на числовій осі на відміну від безлічі натуральних чисел.
Таблиця 1.2
| . | |||||||
| 1/2 | 2/2 | 3/2 | 4/2 | 5/2 | 6/2 | 7/2 | . |
| 1/3 | 2/3 | 3/3 | 4/3 | 5/3 | 6/3 | 7/3 | . |
| 1/4 | 2/4 | 3/4 | 4/4 | 5/4 | 6/4 | 7/4 | . |
| 1/5 | 2/5 | 3/5 | 4/5 | 5/5 | 6/5 | 7/5 | . |
| 1/6 | 2/6 | 3/6 | 4/6 | 5/6 | 6/6 | 7/6 | . |
| 1/7 | 2/7 | 3/7 | 4/7 | 5/7 | 6/7 | 7/7 | . |
| . | . | . | . | . | . | . | . |
Всі раціональні числа можна внести в таблицю з|із| нескінченною|безконечною| кількістю рядків і стовпців (табл. 1.2). Якщо рухатися|сунутися| з|із| лівого верхнього кута|рогу,кутка| по зигзагоподібній траєкторії, нумеруючи по шляху осередку|чарунки,вічка,комірки| числами натурального ряду|лави,низки|, то можна показати взаємно однозначну відповідність між безліччю натуральних і раціональних чисел.
Оскільки раціональні числа щільно заповнюють всю числову вісь, довгий час вважалося|лічилося|, що вони задовольняють всі практичні потреби|нужду| людини і необхідності у введенні|вступі| яких-небудь нових числових множин|безлічі| не існує. Проте|однак| ще старогрецьким|давньогрецьким| математикам вдалося довести існування так званих ірраціональнихчисел, які не можуть бути виражені|виказані,висловлені| у вигляді цілочисельного дробу (несумірні співвідношення).
Відкриття|відчинення| ірраціональних чисел легенда приписує Гиппазію з|із| Метапонта (V вік|повіки| до нашої ери), що входив до кола |коло|піфагорійців – поклонників|прихильників,залицяльників| учення|навчання,вчення| Піфагора. За переказами в той момент, коли|у той момент , коли,в тот момент | Гиппазій дійшов цього відкриття|відчинення|, піфагорійці знаходилися|перебували| у відкритому морі – і вони викинули Гиппазія за борт, звинувативши його в тому, що він привніс у всесвіт|світобудову| елемент, що суперечив|перечив| піфагорійському вченню про те, що всі явища природи можливо звести до цілих чисел або до їх відносин.
Доказ того, що число  несумірно з|із| одиницею, тобто ірраціонально, грецькі математики довели методом від осоружного|противного,супротивного|.
несумірно з|із| одиницею, тобто ірраціонально, грецькі математики довели методом від осоружного|противного,супротивного|.
Приведемо цей доказ. Позначимо:  . Якби
. Якби 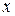 було сумірно з|із| одиницею, то можна було б знайти такі два цілі числа
було сумірно з|із| одиницею, то можна було б знайти такі два цілі числа 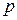 і
і 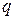 , що
, що  , і тоді ми дійшли б рівності
, і тоді ми дійшли б рівності
 . (1.1)
. (1.1)
Вважаємо|лічимо|, що дріб  несумірна|, інакше ми із самого початку|з самого початку| скоротили б її на загального|спільного| найбільшого дільника чисел
несумірна|, інакше ми із самого початку|з самого початку| скоротили б її на загального|спільного| найбільшого дільника чисел 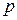 і
і 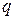 . З правого боку є|наявний| 2 як множник, і тому
. З правого боку є|наявний| 2 як множник, і тому 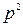 є парне число, і|значить| саме
є парне число, і|значить| саме 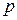 також парне, оскільки|тому що| квадрат непарного числа є непарне число. У такому разі|в такому разі| можна покласти
також парне, оскільки|тому що| квадрат непарного числа є непарне число. У такому разі|в такому разі| можна покласти 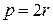 . Тоді рівність (1.1) приймає вигляд|вид|:
. Тоді рівність (1.1) приймає вигляд|вид|:  , або
, або  . Оскільки|тому що| з лівого боку тепер є|наявний| 2 як множник, це означає|значить| що і
. Оскільки|тому що| з лівого боку тепер є|наявний| 2 як множник, це означає|значить| що і 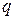 – також парне. Отже, і
– також парне. Отже, і 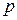 і
і 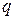 – парні числа, тобто діляться на два, а це суперечить|перечить| допущенню, що дріб
– парні числа, тобто діляться на два, а це суперечить|перечить| допущенню, що дріб  несумірна|.
несумірна|.
Отже, рівність (1.1) неможлива, і  не може бути раціональним числом.
не може бути раціональним числом.
Ірраціональними числами є|з'являються,являються| також число 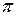 =3,14 – відношення|ставлення| довжини кола до її діаметру і неперово| число e=2,71 – підстава|основа,заснування| натуральних алгоритмів. Ірраціональні числа можуть бути представлені|уявлені| нескінченними|безконечними| неперіодичними дробами.
=3,14 – відношення|ставлення| довжини кола до її діаметру і неперово| число e=2,71 – підстава|основа,заснування| натуральних алгоритмів. Ірраціональні числа можуть бути представлені|уявлені| нескінченними|безконечними| неперіодичними дробами.
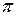 і e – це «зірки», одні з найзнаменитіших чисел на світі. Ординарних, нічим не примітних ірраціональних чисел значно більше. Їх загальна|спільна| кількість в нескінченну|безконечну| кількість раз перевищує рахункову кількість раціональних чисел.
і e – це «зірки», одні з найзнаменитіших чисел на світі. Ординарних, нічим не примітних ірраціональних чисел значно більше. Їх загальна|спільна| кількість в нескінченну|безконечну| кількість раз перевищує рахункову кількість раціональних чисел.
Безліч всіх раціональних і ірраціональних чисел складає безліч дійсних чисел (позначається|значиться| буквою|літерою| R). Кантор довів, що безліч всіх дійсних чисел незліченна. Іншими словами, сукупність всіх дійсних чисел абсолютно іншого типу нескінченності, чим сукупність одних тільки|лише| цілих або одних тільки|лише| раціональних чисел.
Доведемо це фактично. Допустимо, що всі дійсні числа, представлені|уявлені| у вигляді нескінченних|безконечних| десяткових дробів, розташовані|схильні| у порядку|ладі| послідовності, або списку:
1-е число: 
2-е число: 
3-е число: 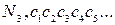
...........................................
де букви|літери|  позначає|значить| цілу частину|частку|, а букви|літери|
позначає|значить| цілу частину|частку|, а букви|літери|  є десятковими знаками, що стоять вправо від коми. Ми допускаємо, що ця послідовність дробів охоплює всі дійсні числа. Істотною|суттєвою| частиною|часткою| доказу є|з'являється,являється| побудова|шикування| за допомогою «діагональної процедури» такого нового числа, щодо|відносно| якого можна показати, що воно не входить в наш список.
є десятковими знаками, що стоять вправо від коми. Ми допускаємо, що ця послідовність дробів охоплює всі дійсні числа. Істотною|суттєвою| частиною|часткою| доказу є|з'являється,являється| побудова|шикування| за допомогою «діагональної процедури» такого нового числа, щодо|відносно| якого можна показати, що воно не входить в наш список.
Побудуємо|спорудимо| таке число. Для цього візьмемо першу цифру після|потім| коми  , яку завгодно|бажано|, але|та| відмінну від
, яку завгодно|бажано|, але|та| відмінну від 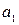 |іншу|, а також від 0 і 9 (останнє – щоб уникнути утруднень|скрути|, що виникають з|із| рівності типу|начеб,немов,немовби| наступного|слідуючого|: 0,999= 1,000); потім другу цифру
|іншу|, а також від 0 і 9 (останнє – щоб уникнути утруднень|скрути|, що виникають з|із| рівності типу|начеб,немов,немовби| наступного|слідуючого|: 0,999= 1,000); потім другу цифру 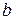 візьмемо відмінною від
візьмемо відмінною від  |іншою|, а також від 0 і 9; третю цифру
|іншою|, а також від 0 і 9; третю цифру 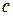 – відмінною|іншої| від
– відмінною|іншої| від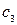 і т.д.
і т.д.
Для більшої визначеності можна умовитися в наступному|слідуючому|: ми беремо  , якщо тільки
, якщо тільки  |лише|, а у випадку
|лише|, а у випадку  візьмемо
візьмемо  ; і аналогічно для всіх інших цифр
; і аналогічно для всіх інших цифр  Тепер розглянемо|розгледимо| число
Тепер розглянемо|розгледимо| число

Це нове число  напевно|обов'язково| не входить в наш список; дійсно, воно не рівне першому числу, що стоїть в списку, оскільки|тому що| від нього відрізняється першою цифрою після|потім| коми, воно не рівне другому числу, оскільки|тому що| від нього відрізняється другою цифрою після|потім| коми, і взагалі відмінно|чудово| від
напевно|обов'язково| не входить в наш список; дійсно, воно не рівне першому числу, що стоїть в списку, оскільки|тому що| від нього відрізняється першою цифрою після|потім| коми, воно не рівне другому числу, оскільки|тому що| від нього відрізняється другою цифрою після|потім| коми, і взагалі відмінно|чудово| від 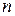 -го числа за списком, оскільки|тому що| від нього відрізняється
-го числа за списком, оскільки|тому що| від нього відрізняється 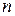 -ою цифрою після|потім| коми. Отже, в нашому списку, складеному ніби то зі|із| всіх дійсних чисел, немає числа
-ою цифрою після|потім| коми. Отже, в нашому списку, складеному ніби то зі|із| всіх дійсних чисел, немає числа  . Це означає|значить|, що безліч всіх дійсних чисел незліченна.
. Це означає|значить|, що безліч всіх дійсних чисел незліченна.
Пізніше за всіх інших була відкрита|відчинена| безліч комплексних чисел, яка позначається|значиться| буквою|літерою| C. Комплексне число записується|занотовується| таким чином: 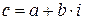 , де
, де  і
і 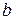 – дійсні числа,
– дійсні числа,  – уявна одиниця. Безліч комплексних чисел рівнопотужна безлічі дійсних чисел.
– уявна одиниця. Безліч комплексних чисел рівнопотужна безлічі дійсних чисел.
Отже, існує, щонайменше, два різних «типу нескінченності»: рахункова нескінченність натуральних чисел і незліченна нескінченність континууму (від латинського continuum – «безперервне») дійсних (і комплексних) чисел. Дискретна математика має справу|річ| з|із| рахунковими множинами|безліччю|. Більш того|більше того|, вона, як правило, має справу|річ| з|із| кінцевими|скінченними| рахунковими множинами|безліччю|.
Читайте також:
- Безперервне литво
- Безперервне розливання
- Вид заняття: лекція
- Вид заняття: лекція
- Вид заняття: лекція
- Вид заняття: лекція
- Вид заняття: лекція
- Вступна лекція
- Вступна лекція 1. Методологічні аспекти технічного регулювання у
- Клітинна селекція рослин.
- Колекція фонограм з голосами осіб, які анонімно повідомляли про загрозу вибуху
- ЛЕКЦІЯ (4): Мануфактурний період світової економіки
| <== попередня сторінка | | | наступна сторінка ==> |
| Придбання ОЗ та НМА | | | Логічні вислови|висловлювання|, зв'язки|в'язки| і операції |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |