• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Сума натуральних чисел

А зараз використовуємо метод індукції для доказу того, що сума перших n позитивних цілих чисел рівна . Якщо n = 1, то, тобто одиниця володіє вказаною властивістю. Припустимо|передбачимо|, що сума перших n – 1 натуральне число також володіє цією властивістю, тобто вона рівна: 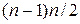. Додавши до цієї суми число n, одержимо|отримаємо|:

.

Таким чином, сума перших n позитивних цілих чисел також володіє вказаною властивістю. Таким чином|значить|, ми можемо стверджувати, що дана формула справедлива для будь-якого натурального n.

Необхідно відмітити|помітити|, що метод індукції дозволяє перевіряти вже відомі формули, але|та| не дозволяє виводити нові формули. Для отримання|здобуття| нових формул доводиться напружувати творчі здібності. Приведемо наступний|такий| історичний приклад|зразок|.

Карл Фредерік Гаус (1777-1855), один з найбільш великих математиків всіх часів і народів, вчився в початковій школі, коли його вчитель|учитель| задав класу завдання|задачу| підсумувати всі цілі числа від 1 до 1000, він розраховував на час відпочинку, поки|доки| його учні будуть зайняті|позичені,посісти| справою|річчю|. Як же було його здивування|подив|, коли Гаус майже миттєво одержав|отримав| правильну відповідь! Його рішення|розв'язання,вирішення,розв'язування| було дуже простим: підсумовуючи перше число з|із| останнім, він одержав|отримав| 1 + 1000 = 1001; підсумовуючи друге з|із| передостаннім: 2 + 999 = 1001 і т.д. Всього сум, рівних 1001, вийшли п'ятсот. Таким чином, відповідь рівна: 500 · 1001 = 1000 · 1001/2 = 500500.

Читайте також:

1. N – чисельність популяції
2. Аксіома неперервності дійсних чисел
3. Алгоритми переведення чисел з однієї позиційної системи числення в іншу
4. Аналіз чисельності, складу і руху персоналу
5. Введення чисел.
6. Визначення добутку на множині цілих невід’ємних чисел, його існування та єдиність. Операція множення та її основні властивості (закони).
7. Визначення суми на множині цілих невід’ємних чисел, її існування та єдиність. Операція додавання та її основні властивості (закони).
8. Визначення чисельності окремих категорій працівників
9. Визначення чисельності окремих категорій працівників
10. Визначення чисельності окремих категорій працівників
11. ВИХІДНІ ТА ПРОГНОЗНІ ЗНАЧЕННЯ ЧИСЕЛЬНОСТІ ХЛОПЧИКІВ ЗА ДАНИМИ ПЕРЕПИСУ
12. Відношення порядку на множині дійсних чисел.

Переглядів: 3074