• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Основні визначення

Ребро в графі G може бути орієнтованим і мати почало|розпочало,зачало| і кінець. Таке ребро називається дугою, а граф, що містить|утримує| дуги, називається орієнтованим, або орграфом|. На малюнку дуга зображається|змальовується| стрілкою.

Багато понять, введених|запроваджених| для неографов|, для орграфов| набувають|придбавають| іншого визначення. Матриця відстаней для орграфа| несиметрична, і ексцентриситет вершини залежить від того, як вибирається максимум. Якщо максимум шукається в рядку, то ексцентриситет вершини називається числом зовнішнього розділення|поділу|, а якщо в стовпці – числом внутрішнього розділення|поділу|. Відповідно визначаються зовнішній і внутрішній центри.

Підстава|основа,заснування| орграфа| – неограф| з|із| тими ж вершинами, але|та| ребрами замість відповідних дуг.

Маршрут в орграфе| – послідовність вершин, сполучених|з'єднаних| дугами, направленими|спрямованими| в один бік.

Маршрут, в якому всі дуги різні, є шлях|колія,дорога|.

Шлях|колія,дорога|, в якому почало|розпочало,зачало| і кінець співпадають|збігаються|, є контур. Довжина шляху|колії,дороги| вимірюється числом вхідних в нього дуг, а для зваженого орграфа| – це сума ваги дуг.

У орграфе| два локальні ступені|міри| вершини v: 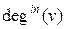– число дуг, що входять в v, і – число дуг, що виходять з|із| v. Лема про рукостискання для орграфа| має вигляд|вид|

, (13.1)

де підсумовування проводиться|виробляється,справляється| по всіх вершинах графа.

Множина 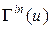вершин v, утворюючих дугу [v, u] з|із| вершиною u, називається множиною попередників вершини u, а множина 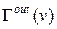вершин u, утворюючих дугу [v, u] з|із| вершиною v, називається множиною наступників|спадкоємців| вершини v. Потужності цих множин|безлічі| відповідно рівні:, .

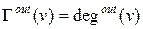Надалі під графом розумітимемо як неограф|, так і орграф|.

13.2. Маршрути в орграфе|

Завдання|задачі|, пов'язані з маршрутами в орграфе|, мають велике практичне значення, що і дає стимул до розвитку і вдосконалення методів їх рішення|розв'язання,вирішення,розв'язування|. Найчастіше встає питання про мінімальні і максимальні відстані, про число маршрутів певної довжини.

Приклад|зразок| 13.1. Заданий орграф| (мал. 13.1). Скільки в ньому маршрутів завдовжки 3?

Мал. 13.1

Рішення|розв'язання,вирішення,розв'язування|. Використовуємо алгебраїчний метод рішення задачі, на підставі теореми 12.4. Запишемо матрицю суміжності. Матриця суміжності орграфа| – несиметрична.

, .

Піднесемо цю матрицю до ступеня 3. Підсумовуючи всі елементи одержаної|отриманої| матриці, знаходимо|находимо|, що число маршрутів завдовжки 3 рівне восьми. Три одиниці, що стоять по діагоналі, показують, що сюди входить 3 помічених|позначених| контури. Очевидно, що це контури: 1–4–3, 4–3–1, 3–1–4.

Читайте також:

1. I визначення впливу окремих факторів
2. II. Визначення мети запровадження конкретної ВЕЗ з ураху­ванням її виду.
3. II. Мотивація навчальної діяльності. Визначення теми і мети уроку
4. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
5. Ocнoвнi визначення здоров'я
6. Адвокатура в Україні: основні завдання і функції
7. Алгебраїчний спосіб визначення точки беззбитковості
8. Амортизація основних засобів, основні методи амортизації
9. Аналіз службового призначення деталей та конструктивних елементів обладнання харчових виробництві, визначення технічних вимог і норм точності при їх виготовленні
10. Аналіз стратегічних альтернатив та визначення оптимальної стратегії формування фінансових ресурсів
11. Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
12. Артеріальний пульс, основні параметри

Переглядів: 474