Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

ЛЕКЦІЯ 5

Канонічна модель плану станції (частина 1)

Канонічна модель плану колійного розвитку станції повинна забезпечити:

– вхідний контроль введеної інформації;

– можливість зміни окремих параметрів схеми, заданих за умовчанням;

– аналіз, автоматичне розпізнавання типових елементів схеми колійного розвитку і вибір програмних модулів для розрахунку;

– комплексний розрахунок плану колійного розвитку і побудова вихідної моделі.

Для реалізації процедур автоматизованого синтезу колійного розвитку станцій найбільш прийнятними є ГМ, що засновані на зважених орграфах. До складу канонічної моделі станції повинні входити топологічна і параметрична моделі. Топологічна модель відображає склад елементів станції (колії, стрілочні переводи, сполучні криві та ін.), їх взаємне розташування і взаємозв'язок. Параметрична модель містить відомості про форму і геометричні розміри відповідних елементів.

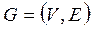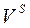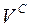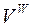Топологічна модель станції є орієнтований граф , в якому виділено три підмножини вершин: , і . Вершини 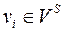є центрами стрілочних переводів (ЦП), вершини 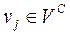– вершинами кутів повороту кривих (ВКП), вершини 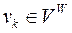– кінцями колій (КК). Дуга графа позначається впорядкованою парою, що складається з початкової і кінцевої 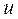вершин; її напрям задано від вершини до вершини 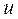. Прийнято, що всі дуги орієнтовані зліва направо.

Ступінь вершини орієнтованого графа 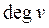визначається числом інцидентних їй дуг

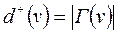де – відповідно напівступені виходу і заходу вершини , які визначаються як множина всіх дуг, що виходять з вершини і заходять в неї,

і ,

де 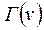– множина вершин, що є кінцевими вершинами дуг, у яких початковою вершиною є ;

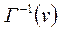– множина вершин, що є початковими вершинами дуг, у яких кінцевою вершиною є .

Напівступені вершин 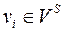орієнтованого графа дозволяють ідентифікувати тип вершини (ЦП – , BКП – 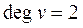, KК – 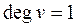), а також визначити напрям укладання стрілочних переводів (якщо 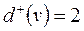і – перевід протишерстний; якщо і – перевід пошерстний). Максимальний напівступінь кожної вершини не перевищує двох.

Згідно з теорією графів сума напівступенів виходу всіх вершин графа дорівнює сумі напівступенів заходу і дорівнює числу його дуг

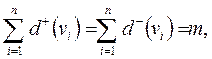
де , 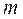– відповідно число вершин і дуг графа .

Дане твердження використовується для вхідного контролю даних про схему станції.

Для представлення орієнтованого графа станції в ЕОМ прийнята структура даних, що називається списками інцидентності. Вказані списки містять для кожної вершини 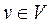список вершин 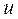таких, що 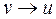. При цьому, оскільки напівступінь виходу кожної вершини графа не перевищує двох, то для представлення кожного списку достатньо двох змінних в пам'яті ЕОМ.

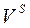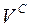Для розділення множини вершин графа на підмножини , і 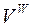кожному з них виділені непересічні групи номерів: , , .

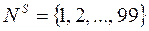Нижче наведено приклад списків інцидентності вершин 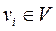графа , показаного на рис. 2 (табл. 3).

Перший стовпець матриці є списком всіх вершин графа; в рядках двох інших стовпців – списки інцидентності відповідних вершин.

Таблиця 3 – Списки інцидентності вершин орграфа


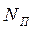
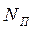
+14		+3

+4
	+18





+1

Для зручності аналізу схем станцій прийнято, що першим в списку для вершин 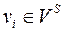з напівступенем виходу 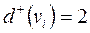(протишерстні переводи) указується номер вершини 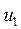, з якою дана стрілка (вершина 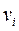) зв'язана по прямій колії (звичайний перевід) або правій колії (симетричний перевід); другим в списку указується номер іншої вершини 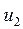, суміжної з .

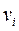Для вершин 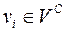з напівступенем виходу 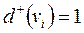(ВКП, ЦП пошерстних стрілок) другий елемент списку відсутній. Для вершин 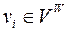з напівступенем виходу 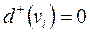(КК) відсутні обидва елементи списку.

Рисунок 2 – Орграф G=(V,E) схеми станції А

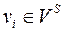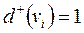Слід зазначити, що при прийнятому способі представлення орграфа для деяких вершин , (ЦП пошерстних стрілок) неможливо визначити з моделі кути нахилу суміжних відрізків. Тому за наявності вхідної моделі, ці кути встановлюються на підставі екранних координат вершин відрізків, а при табличному введенні внутрішньої моделі в списках інцидентності необхідно кінцеві вершини дуг, що заходять в такі ЦП по прямій колії, помітити знайомий «+».

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Види та призначення геометричних моделей	\|	ЛЕКЦІЯ 6

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.