• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Загальна постановка задачі в багатокритеріальних системах

Моделювання систем

Лекція 7

Запитання для самоперевірки

1. Охарактеризуйте етапи формування цілей.

2. Поясніть структуру локальних цілей.

3. Що означає поняття додаткові локальні цілі?

4. Поясніть принцип створення системи локальних цілей.

5. Поясніть способи досягнення декількох локальних цілей.

6. Охарактеризуйте типові схеми зв’язків між локальними цілями.

При постановці завдань оптимізації потрібно, насамперед, визначити цілей (або кілька цілей), переслідувану суб'єктами керування, і встановити, якими характеристиками (змінними) системи (або процесу) можна оперувати, тобто які змінні можна розглядати в якості керуючих параметрів.

Під метою будемо розуміти той кінцевий результат, який розраховують одержати суб'єкти керування за допомогою вибору керуючих впливів на досліджувану систему.

Після того як ціль визначена, необхідно знайти оптимальний спосіб дій кожного суб'єкта керування, що забезпечує її досягнення. Якщо для системи визначено кілька цілей розвитку, то потрібно вказати принцип оптимальності, який дозволяв би виділяти рішення, найкращі в змісті досягнення цих цілей.

Наступним важливим моментом є завдання безлічі припустимих впливів на систему з боку суб'єкта керування – безлічі керованих змінних. Будь-який набір припустимих впливів будемо називати рішенням.

При побудові математичних моделей функціонування й розвитку навіть порівняно невеликих реальних систем ми зустрічаємося з необхідністю обліку складних взаємозв'язків компонент моделі, що виявляють діючий вплив на реалізацію альтернатив розвитку й досягнення поставлених цілей. Внутрішні між комплексні зв'язки системи можуть бути описані за допомогою деякого кінцевого графа G = (Z,G), вершинами якого служать компоненти моделі.

Графом називають пари G = (Z,G), у якій безліч вершин позначена через Z, а безліч дуг (ребер) задане вираженням G : Z → Z . Для спрощення аналізу графів вершини їх звичайно нумерують. У цьому випадку, якщо i і j – номера

суміжних вершин, то ребро графа може бути задане парою (i, j). Якщо всі ребра графа задані впорядкованими парами, то такий граф називають орієнтованим.

На графові між комплексних зв'язків G, виходячи з опису системи, доцільно виділити основні компоненти моделі, на які суб'єкт керування може виявляти безпосередній вплив компоненти, що й супроводжують, стан яких однозначно визначається станом основних компонентів. Розглянемо деякі приклади керування складними системами.

Приклад 1. Трохрівнева система керування гнучкою автоматизованою ділянкою.

У загальному випадку гнучке автоматизоване виробництво (ГАВ) являє собою систему, що включає наступні компоненти:

- автоматизовані технологічні модулі (верстати, лінії, ділянки);

- автоматизований транспорт;

- автоматизовані склади.

Керування роботою цих компонентів і здійснення зв'язків між ними забезпечує система керування ГАВ. З її допомогою здійснюються запуск, керування й контроль над роботою технологічного встаткування, синхронізація виконуваних робіт, оптимізація завантаження встаткування, формується графік роботи транспортних засобів, автоматизованих складів і т.п.

Як правило, СУ ГАВ має ієрархічну структуру. Найпоширенішою структурою системи керування гнучкою автоматизованою ділянкою є трьохрівнева (рисунок 7.1).

Верхній рівень вирішує завдання організаційно-економічного характеру й ухвалює довгострокові рішення; проводить розрахунок змінно-добових завдань по кожній одиниці верстатного встаткування, завдань по технологічній підготовці ділянки; ураховує запас заготовок, інструмента й пристосувань на складі; накопичує інформацію для різних служб цеху, Середній рівень здійснює контроль над роботою мікропроцесорних систем; ухвалює оперативні рішення відповідно до вступники від підсистем нижнього рівня інформацією; виробляє керуючі впливи на ці підсистеми.

Нижній рівень забезпечує за допомогою мікропроцесорних систем безпосереднє керування технологічним процесом.

Аналіз і керування роботою такої ділянки вимагає рішення значної кількості оптимізаційних багатокритеріальних завдань, завдань сіткового планування, транспортних завдань, завдань розміщення і т.д.

Приклад 2. Проектування оптимального програмного комплексу.

При проектуванні програмного комплексу необхідно забезпечити виконання ряду вимог: збільшити точність завдання вхідних впливів, скоротити обсяг оперативної пам'яті, зменшити час роботи програм, зменшити завантаження каналів зв'язки між ЕОМ і зовнішніми запам'ятовувальними пристроями і т.д.

Припустимо, що програмний комплекс повинен реалізувати безліч операцій σ = σ₁, σ₂, ..., σm. Під операцією ми розуміємо, наприклад, рішення системи диференціальних або алгебраїчних рівнянь конкретного виду, знаходження екстремуму деякої функції, пошук інформації в заданому масиві й т.п.

Кожна операція 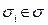може бути реалізована кожний із програм деякого заданого безлічі πi= (π_i1, π_i2, ..., π_ij).

i = 1, 2, ..., M.

Програми відрізняються друг від друга по своїх характеристиках, що впливають на виконання вимог до комплексу в цілому. Програмний комплекс являє собою впорядкований набір програм.

.

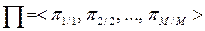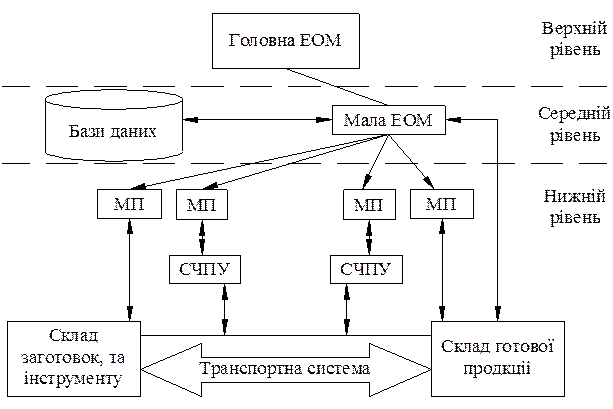
Рис. 7.1. Принципова схема трохрівневої системи керування гнучкою автоматизованою ділянкою

При його розробці враховується вектор критеріїв H = (H₁, H₂, …, H_m) тому оцінка якості комплексу є векторною величиною.

Безліччю припустимих керувань є безліч π = π1 ×...× πm . Відображення H : π → Е_m задає правило, але якому кожному набору програм (або варіанту програмного комплексу) відповідає векторна оцінка. Таким чином, завдання проектування оптимального програмного комплексу є багатокритеріальним завданням оптимального керування.

Апаратна реалізація системного аналізу припускає виробіток стандартних приймань моделювання процесу прийняття рішень у складній системі й загальних способів роботи з побудованими моделями.

Більшість ситуацій, пов'язаних із проблемою ухвалення рішення в складній системі, полягає в тому, що з наявного безлічі варіантів рішення (припустимих керувань) необхідно виділити деяка підмножину варіантів, що є більш кращими. Правило, по якім установлюється перевага в безлічі рішень, називається принципом оптимальності.

Зазначені елементи – безліч варіантів рішення й принцип оптимальності – дозволяють формалізувати процес ухвалення рішення. Відсутність одного із цих елементів повністю позбавляє завдання змісту.

Позначимо безліч варіантів рішення через Ω. Елементи безлічі називають іноді також альтернативами.

Читайте також:

1. I. Загальна характеристика політичної та правової думки античної Греції.
2. Ni - загальна кількість періодів, протягом яких діє процентна ставка ri.
3. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
4. Алгоритм розв’язання задачі
5. Алгоритм розв’язання розподільної задачі
6. Алгоритм розв’язування задачі
7. Алгоритм розв’язування задачі
8. Алгоритм розв’язування задачі
9. Алгоритм розв’язування задачі
10. Алгоритм розв’язування задачі
11. Алгоритм розв’язування задачі
12. Алгоритм розв’язування задачі оптимізації в Excel

Переглядів: 1053