• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Переріз і об’єднання множин. Закони цих операцій. Доповнення підмножини

У ряді задач теоретичного і практичного змісту виникає потреба виконувати над множинами певні операції.

Означення: Перерізомдвох множин А і В називається множина, яка містить усі ті і тільки ті елементи, які належать кожній із цих множин.

Позначають переріз множин за допомогою знака ∩. Отже, якщо

а є А∩В, то а є А і а є В; тобто А∩В = {x | x є A і х є В}.

Якщо перерізом множин А і В є порожня множина, тобто А∩В = Ø, то вважають, що множини не перетинаються. Якщо ж множина А є підмножиною множини В, то А∩В = А.

Наприклад: Якщо множина А – це дільники числа 18, В – дільники 24, то А∩В = {1, 2, 3, 6}.

Переріз зручно проілюструвати за допомогою кругів Ейлера:

А∩В А∩В = ø

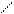
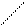
А В А В

Означення: Об’єднанням двох множин А і В називається множина, яка містить усі ті і тільки ті елементи, які належать хоча б одній із множин А або В. Об’єднання множин позначають знаком U :

А U B = {x| x ЄА або х Є В}.

Наприклад: A = {a, b, c, d}, B = {k, m, n}

A U B = {a, b, c, d, k, m, n}.

А U B А U B

Означення: Якщо множина В є підмножиною множини А, то доповненням множини В до множини А називається така множина А\В, що містить ті і тільки ті елементи множини А, які не належать множині В.

Тобто: А\В = {x | х є А і х В}.

А\В

Наприклад: А = {a, b, c, d, e, f}, B = {a, b, d, f}. Тоді А\В = {c, e}.

Оскільки операції перерізу, об’єднання та доповнення відповідають діям множення, додавання і віднімання, то для них виконуються всі закони цих дій, тобто переставний, сполучний та розподільний.

1. Переставний: а) А∩В = В∩А;

б) АUB = BUA.

2.Сполучний: а) (А∩В)∩C = A∩(B∩C);

б) (АUB)UC = AU(BUC).

Доведемо рівність б). Для того щоб множини (АUB)UC і AU(BUC) були рівні, необхідно і достатньо, щоб будь-який елемент х, що належить першій множині, належав також і другій, і навпаки.

1) Нехай х належить першій множині, тобто х (АUB)UC. Тоді х АUB, або х С (за означенням об’єднання множин). Звичайно, може бути і одночасно х АUB і х С, але для доведення це неістотно.

А) Якщо х АUB, то знову за означенням об’єднання множин або х А і тоді х AU(BUC), або х В і тоді х BUC, а отже , і х AU(BUC);

Б) Якщо х С, то х ВUС, тому х AU(BUC).

Таким чином, довели, що будь-який елемент першої множини (лівої частини рівності) належить і другій множині (правій чистині рівності). Аналогічно виконується друга частина доведення.

2) Нехай, навпаки, будь-який елемент х належить другій множині, тобто х AU(BUC). Доведемо, що тоді х (АUB)UC.

Якщо х AU(BUC), то або х А, тоді х АUB, а отже і х (AUB)UC; або х BUC, але тоді або х B, а отже, і х AUB, тому х (АUB)UC, або х С, але тоді х (АUB)UC.

Тотожність доведено.

3. Розподільний: a) (AUB)∩C = (A∩C) U (B∩С);

б) А∩(В\С) = (А∩В)\ (А∩С);

в) (А∩В)UC = (AUC)∩(BUC).

Читайте також:

1. I. Доповнення до параграфу про точкову оцінку параметрів розподілу
2. IV. Закони ідеальних газів.
3. VI. ДОПОВНЕННЯ ДО ЗОБРАЖЕНЬ
4. А АА1В1В – осьовий переріз
5. А) Грошовий обіг. Закони.
6. Аграрні закони України
7. Антитоталітарні демократичні революції у країнах Східної Європи. Розпад Югославії. Об’єднання Німеччини
8. База управлінських рішень і закони організації.
9. Банківські об’єднання
10. Булеві теореми та закони
11. В процесі читання виділіть маркером або підкресліть найважливіші, на вашу думку, екологічні закони.
12. В) економічні категорії і закони.

Переглядів: 13015