• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Система вправ

1. Два гуртки – зоологічний та ботанічний – об’єднались в один гурток юних натуралістів. Множина учнів, що займались у зоологічному гуртку: А = {Соколова, Волкова, Білова, Андрєєв, Іванов, Михайлова}. Множина учнів, які займались у ботанічному гуртку: В = {Іванов, Михайлова, Орлова, Єрмакова}.

а) Напишіть множину членів гуртка юних натуралістів;

б) Знайдіть кількість елементів множин А, В, А 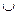В;

в) Чи є правильною рівність n(A) + n(B) = n(А 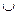В)?

2. У першому класі учні знайомляться із записами: 1 + 1 = 2, 2 + 1 = 3, 3+2=5. Які теоретико-множинні поняття при цьому неявно використовуються?

3. Замість зірочки (*) поставте знак =, < або > , що отримати істинне висловлення:

а) 4968 + 7369 * 4968 + 7370;

б) 2819 + 6785 * 2820 + 6734;

в) 71598 + 39 * 71600 + 36.

4. Які умови повинні виконуватись для множин А і В, щоб були істинними висловлення:

а) n(A) + n(B) > n(А 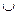В);

б) n(A) + n(B) = n(A);

в) n(A) + n(B) = n(В).

5. Дано множини B = {0, 1, 2, 3, 4, 5} і D = {0, 2}.

а) Знайдіть: n(B), n(D), n(B\D), n(B) – n(D);

б) Чи є істинним висловлення n(B) – n(D) = n(B\D);

в) У якому відношенні повинні знаходитись множини А і В, щоб n(A) – n(B) = n(A\B)?

6. Чи може різниця двох цілих невід’ємних чисел:

а) дорівнювати від’ємнику;

б) дорівнювати зменшуваному?

7. Виконати дії раціональним способом, пояснити застосовані властивості: а) 17527 – (2080 + 4527), в) (5762 + 416) + 1238,

б) (527 +658) + (342 + 173), г) (6902+899) – 349.

8. Запишіть суму у вигляді добутку:

а) 5607 + 5607 + 5607 + 5607 + 5607;

б) (34 + 78) + (34 + 78) + (34 + 78) + (34 + 78);

в) х + х + х + х + х + х + х + х + х + х;

г) (у +7) + (у +7) + (у +7) + (у +7) + (у +7) + (у +7).

9. Запишіть у вигляді суми:

а) 384 ∙ 9; в) 0 ∙ 8; д) (а + 7) ∙ 4; ж) 5²;

б) 1 ∙ 10; г) а ∙ 5; е) (с + b) ∙ 7; з) а².

10. Обчисліть раціональним способом, використовуючи комутативний закон множення:

а) 5 ∙ 3764 ∙ 2; в) 8 ∙ 5379 ∙ 125;

б) 4 ∙ 6978 ∙ 25; г) 4 ∙ 375 ∙ 250.

11. Обчисліть частку двома способами:

а) (390 + 39) : 13; в) (64 ∙ 32) : 8;

б) (270 + 37) : 37; г) 1470 : ( 147 : 3).

Підкресліть раціональний спосіб. Відповідь обґрунтуйте.

2. Скласти усі види простих задач, які б розв’язувались наступною дією: а) 8 + 5; б) 17 – 9; в) 7 ∙ 4; г) 24 : 8.

13. Скласти задачу на ділення на рівні частини і переробити її так, щоб дістати ще дві задачі: на ділення на вміщення і на зменшення числа у кілька разів.

14. Знайти НСК і НСД чисел: а) 1320 і 385, б) 1820 і 858.

15. Виконати дії з докладним коментуванням:

а) 645 б) 364 в) _928 г) 14724 36

⁺189^× 73459

16. Які з висловлень істинні, а які хибні? Поясніть чому.

а) 273 кратне числу 5;

б) 273 не кратне числу 5;

в) 3 є дільником числа 273;

г) Не правильно, що 3 є дільником числа 273.

17. Доведіть, що при будь-якому невід’ємному значенні n число n³ – n ділиться на 3.

18. Довести, що з трьох послідовних натуральних чисел одне і тільки одне з них ділиться на 3.

19. Запишіть числа 245₃, 1372₈, 11001₂ у вигляді суми степенів основи системи числення.

20. Які з чисел записані правильно, а як і ні: 3114₅, 3756₈, 121211₂, 12101₃?

21. Перевести число з десяткової системи числення в іншу і виконати перевірку: а) 214₁₀ = ... ₇ ; б) 305₁₀ = ... ₈.

22. Які цифри повинні стояти замість зірочок (числа записані в десятковій системі числення)?

а) ₊*246 б) _ *3*8

3*1*123*

4960 4143

23. Прочитайте і запишіть в десятковій системі числення наступні числа: III, IV, VIII, IX, XL, L, CM, C, M, XXXIX, CCCXXXVIII.

24. Запишіть в римській нумерації числа: 38, 41, 102, 1979, 2009.

25. При діленні цілого невід’ємного числа а на натуральне число b дістанемо неповну частку q і невід’ємну остачу r . Знайти:

а) q і r , якщо а = 112, b = 36,

б) b і q, якщо а = 100, r = 6,

в) b і r , якщо а = 351, q = 14.

Читайте також:

1. Active-HDL як сучасна система автоматизованого проектування ВІС.
2. D. СОЦИОИДЕОЛОГИЧЕСКАЯ СИСТЕМА ВЕЩЕЙ И ПОТРЕБЛЕНИЯ
3. II. Бреттон-Вудська система (створена в 1944 р.)
4. III. Вправи з початкового положення стоячи.
5. III. центральная нервная система
6. ISO9000. Як працює система управління якістю
7. IV. Система зв’язків всередині центральної нервової системи
8. IV. УЗАГАЛЬНЕННЯ І СИСТЕМАТИЗАЦІЯ ВИВЧЕНОГО
9. The educational system of Great Britain (Система освіти Великобританії)
10. V. Виконання вправ на застосування узагальнювальних правил.
11. V. СИСТЕМА ПОТОЧНОГО ТА ПІДСУМКОВОГО КОНТРОЛЮ ЗНАНЬ СТУДЕНТІВ
12. V. Систематизація і узагальнення нових знань, умінь і навичок

Переглядів: 800