Площа фігури, її властивості і вимірювання

Задача вимірювання площі – одна з найдавніших задач практики. Люди у давнину вимірювали площі земельних ділянок, з кожної одиниці площі вони платили податки. У стародавньому Єгипті після весняного розливу Нілу і спаду води потрібно було відновлювати межі ділянок, а для цього необхідно було вміти вимірювати їх площі. В стародавні часи одиницями площі були: колодязь – площа, яку можна полити з одного колодязя, соха або плуг – середня площа, що оброблена за день сохою чи плугом. (Слово «геометрія» – грецьке, у перекладі означає «землемірство»).

Площею фігури називається додатна величина, яка визначена для кожної фігури так, що:

1) рівні фігури мають рівні площі;

2) якщо фігура складається із скінченої кількості фігур, то її площа дорівнює сумі їх площ.

Якщо порівняти дане означення з означенням довжини відрізка, то маємо, що для площі характерні ті ж самі властивості, що і для довжини, але задані вони на різних множинах: довжина – на множині відрізків, а площа – на множині плоских фігур.

За одиницю площі приймають площу квадрата, довжина сторони якого дорівнює одній лінійній одиниці: 1 м² (площа квадрата із стороною 1 м), 1 см², 1 мм².

Якщо довжину лінійної одиниці позначено через е, то відповідну їй одиницю площі зручно позначити через е².

Вимірювання площі полягає в кратному порівнянні площі даної фігури F з площею одиничного квадрата е². Результатом порівняння буде число n таке, що

S_ф= n ∙ e² => m_e (F) = n, де n – числове значення площі.

Властивості площі:

1. Якщо фігури рівні, то рівні і числові значення їх площ (при однаковій одиниці площі).

Фігури, площі яких рівні, називаються рівновеликими.

2. Якщо фігура F складається з фігур F₁, F₂, ..., F_n, то числове значення площі фігури F дорівнює сумі числових значень площ фігур F₁, F₂, …, F_n (при однаковій одиниці площі).

3. При заміні одиниці площі числове значення площі збільшується (зменшується) у стільки ж разів, у скільки ж нова одиниця менша (більша) від старої.

Щоб на практиці вимірювати площу використовують палетку – сітку квадратів на прозорому матеріалі. Для вимірювання палетку накладають на фігуру, площу якої знаходять. Якщо виміри прямокутника – цілі числа, палетка накладається так, щоб її лінії сумістились із сторонами прямокутника. Далі підраховують число квадратів, що вміщуються в прямокутнику.

Якщо фігура складніша, то є два способи визначення площі за допомогою палетки.

І спосіб. Спочатку порахувати кількість цілих квадратів, що знаходяться у середині фігури F. Їх кількість m. А потім порахувати кількість нецілих квадратів, тобто число n. Тоді площа фігури F буде обчислена за формулою:

S (F) ≈ (m + n : 2) ∙ е ².

ІІ спосіб. Також полічити кількість цілих квадратів у середині фігури, їх m. Потім полічити найбільшу кількість квадратів, що містять у собі фігуру, нехай їх k, тоді

m ∙ е ²< S (F) < k ∙ е ².

Тобто значення S буде десь посередині між числами m i k. Тому треба знайти середнє арифметичне

S ≈ 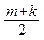∙ е ².

В обох способах значення площі будуть співпадати: k = m + n

S ≈ ( 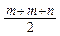) ∙ е ² = ∙ е ² = (m + 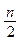) ∙ е ².

У підручниках з математики початкових класів за допомогою палетки учні знаходять площі різних фігур. Наприклад:

У даній таблиці подано одиниці вимірювання площі, які застосовуються найчастіше:

1мм² – площа квадрата, сторона якого 1мм

1см² – площа квадрата, сторона якого 1см

1дм² – площа квадрата, сторона якого 1дм

1м² – площа квадрата, сторона якого 1м

Ар (а) – площа квадрата, сторона якого 10м (сотка)

Гектар (га) – площа квадрата, сторона якого 100м

1км² – площа квадрата, сторона якого 1км

Між одиницями площі існують наступні співвідношення:

1см² = 100мм² 1 дм² = 100см²

1м² = 100дм² 1 а = 100м²

1га = 10000м² 1 км² = 1000000м²

За Програмою початкових класів у 4 класі учні знайомляться з правилом обчислення площі прямокутника:

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Довжина відрізка, її властивості і вимірювання	\|	Щоб обчислити площу прямокутника, треба визначити його довжину і ширину та знайти добуток цих чисел.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.