• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Довжина відрізка, її властивості і вимірювання

Властивість предметів мати протяжність називається довжиною.А також довжиною відрізканазивається додатна величина, яка визначається для кожного відрізка так, що:

1) рівні відрізки мають рівні довжини;

2) якщо відрізок складається із кінченої кількості відрізків, то його довжина дорівнює сумі довжин цих відрізків.

Розглянемо процес вимірювання довжин відрізків. З множини відрізків вибирають будь-який відрізок e і приймають його за одиницю довжини. На відрізку а від одного його кінця відкладають послідовно відрізки, що дорівнюють e до тих пір, поки це можливо. Якщовідрізки, що дорівнюють e, відкладаються n раз і кінець останнього співпав з кінцем відрізка а, то кажуть, що значення довжини відрізка а – це натуральне число n і пишуть: а = nе.

Якщож відрізки, що дорівнюють e відклалися n раз і ще залишилась остача, яка менша e, то на ній відкладають відрізки, що дорівнюють

e₁= e.

Якщовони відклалися точно n₁ раз, тоді а= n,n₁е і значення довжини відрізкаа–цескінчений десятковий дріб.

Якщовідрізокe₁відклали n₁ раз і залишилась остача, яка меншаe_1, то на ній відкладають відрізки, що дорівнюють

е₂= e.

Якщо цей процес продовжувати далі, то отримаємо, що значення довжини відрізка а – це нескінченний десятковий дріб.

Отже, при вибраній одиниці довжина будь – якого відрізка виражена додатнім дійсним числом.

Правильне і обернене твердження:

якщо дано додатне число n,n₁n₂…, то при побудові відрізка його числове значення довжини буде рівне дробу n,n₁n₂...

Отже, маємо основну властивість довжин відрізків:

при вибраній одиниці довжини довжина будь-якого відрізка виражена додатнім дійсним числом і, навпаки, для кожного додатного дійсного числа існує відрізок, довжина якого виражена цим числом.

Зауважимо, що коли в результаті вимірювання маємо нескінчений десятковий дріб, то значення довжини відрізка вважається наближеним.

Сформулюємо інші властивості довжин відрізків:

1. Якщо два відрізка рівні, то числові значення їх довжин теж рівні і, навпаки, якщо числові значення довжин двох відрізків рівні, то і рівні самі відрізки, тобто

а = b 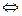m_e (a) = m_e (b).

2. Якщо даний відрізок – це сума декількох відрізків, то числове значення його довжини дорівнює сумі числових значень довжин відрізків-доданків і, навпаки, якщо числове значення довжини відрізка дорівнює сумі числових значень декількох відрізків, то і сам відрізок дорівнює сумі цих відрізків, тобто

с = а + b 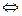m_e (с) = m_e (a) + m_e (b).

3. Якщо довжини відрізків а і b такі, що b = х · а, де х – додатне дійсне число і довжина відрізка а виміряна за допомогою одиниці е, то для того, щоб знайти числове значення довжини відрізка b при одиниці е, достатньо число х помножити на числове значення довжини відрізка а при одиниці е, тобто

b = х · а m_e (b) = х · m_e (а).

4. При зміні одиниці довжини числове значення довжини збільшиться (або зменшиться) в стільки ж разів, в скільки збільшиться (або зменшиться) нова одиниця відносно старої.

З даних властивостей маємо:

5. а < b 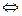m_е (а) < m_е (b),

а > b 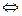m_е (а) > m_е (b);

6. с = а − b 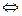m_e (с) = m_e (a) − m_e (b);

7. х = а : b х = m_e (a) : m_e (b).

Розглянуті властивості дозволяють порівнювати довжини відрізків та дії над ними зводити до порівняння та дій над відповідними числовими значеннями довжин цих відрізків.

Приклади:

1) 15м < 15, 1м, бо 15 < 15, 1;

2) 6, 5см + 4, 8см = (6, 5 + 4, 8) см = 11, 3см;

3) 14 · 2 дм = (14 · 2) дм = 28дм.

Найдавніші одиниці довжини ототожнювались з назвами частин людського тіла. Наприклад: ширина чотирьох пальців – долоня, довжина ліктя – лікоть, довжина ступні – фут, довжина суглоба великого пальця – дюйм, довжина фаланги вказівного пальця – вершок.

У XV – XVI ст. у ряді країн були одиниці, пов’язані між собою. У Росії одиницями довжини були миля, верства, сажень і аршин:

1миля = 7 верств,

1 верства = 500 сажнів,

1 сажень = 3 аршина.

У метричних одиницях 1 аршин ≈ 71,12см.

Основою для міжнародної системи мір стала нова система одиниць вимірювання величин, створена у Франції у 18 столітті. За основну одиницю довжини в цій системі мір було взято метр – одна сорокамільйонна частина довжини земного меридіана, який проходить через Париж. Тому було виготовлено платиновий еталон метра – лінійку з нанесеними штрихами на її кінцях, що зберігається в Національному архіві Франції та має назву «архівного метра».

Метрична система мір не одразу дістала визнання: у 1875 р. нею користувались 17 держав, а зараз – 60. У Росії ця система почала використовуватись з 1899 р., а в Україні – з 1925 р.

При сучасних вимірюваннях довжин використовують такі одиниці як міліметр (мм), сантиметр (см), дециметр (дм), метр (м), кілометр (км), між якими існують відповідні співвідношення:

1м = 100см 1км = 1000м

1м = 10дм 1 дм = 10см

1м = 1000мм 1см = 10мм

Читайте також:

1. OПТИЧНІ ВЛАСТИВОСТІ КОЛОЇДНИХ СИСТЕМ
2. А) Товар і його властивості.
3. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
4. Аеродинамічні властивості колісної машини
5. Алкани (насичені вуглеводні). Хімічні властивості алканів
6. Алкани, їх хімічні властивості.
7. Алкени. Хімічні властивості
8. Алкіни. Хімічні властивості
9. Алфавітний підхід до вимірювання кількості інформації.
10. Аміни. Фізичні та хімічні властивості аліфатичних амінів.
11. Аналізатори людини та їхні властивості.
12. Аналізатори людини та їхні властивості.

Переглядів: 4958