Прикладні задачі теорії графів для транспортних систем

Найбільш розповсюдженими прикладами використання теорії графів у сфері створення та експлуатації транспортних систем є:

- формування раціональної структури транспортного обслуговування держави, регіону або міста (докладно розглядається в [1,16 ]);

- граф станів вагона та локомотива робочого парку, наприклад [ 19];

- визначення тарифної відстані у роботі підрозділів служби маркетингу та комерційної роботи;

- граф станційних маршрутів;

- критичний шлях при використанні сітьових графіків тощо.

9 Потоки в мережах

9.1 Загальні поняття

Граф, елементам якого поставлені у відповідність деякі параметри, називають зваженим графом або мережею. Параметри можуть бути задані на таких елементах, як вершини, дуги, підмножини вершин і дуг.

Розрізняють транспортні, інформаційні, електричні, гідравлічні мережі. Для характеристики мереж застосовується деякі поняття – функції на вершинах і дугах. Кожна вершина i характеризується інтенсивністю d (i). Вершини, для яких d (i)>0, називаються джерелами, а на яких d (i)<0 – стоками, інші вершини нейтральні, тобто на транспортній мережі джерела - станції навантаження (відправники), стоки – станції вивантаження (одержувачі). Для характеристики дуг введемо функцію пропускної спроможності, що ставить у відповідність кожній дузі (i, j) U графа G (I, U) ненегативне ціле число τ (i, j), називане пропускною спроможністю дуги. Для транспортних мереж це максимальна кількість вантажу, яку відповідна комунікація може пропустити за одиницю часу, тобто в мережі G (I,U) з одним джерелом S і одним стоком t задана функція пропускної спроможності τ (i, j), те в ній може бути задана також функція називана потоком.

9.2 Задача про максимальний транспортний потік

Потоком у мережі називається функція, що зіставляє з кожною дугою (i, j) ціле число x (i, j) і має властивості:

(9.1)

(9.2)

(9.3)

Для мережі потік x (i, j) по дузі (i, j) – це кількість тонн вантажу, що проходить через цю дугу в одиницю часу. Потоком у мережі називається сукупність {x (і, j)} потоків по всіх дугах мережі. Умова перша означає, що потік по кожній дузі ≥0 (ненегативний) і не перевищує пропускної спроможності дуги, (τ) – що кількість вантажу, що протікає в будь-яку нейтральну вершину мережі, дорівнює кількості вантажу, що випливає з її, тобто загальна кількість вантажу, що випливає зі стоку S дорівнює загальній кількості вантажу, що притікає в стік t (умова 3).

Лінійна її форма – величина потоку в мережі.

Розріз Розглянемо мережу G (I,U) з одним джерелом S і одним стоком t.

Якщо розбити безліч усіх вершин мережі G на дві непересічних підмножини R і R, то розрізом мережі, що відокремлює S від t називається сукупність усіх дуг (R, R), де S 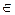R, а t 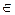R.

Тобто розріз складають усі ті і тільки ті дуги, що виходять з вершин і 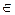R і закінчуються у вершинах j 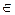R.

Сума пропускних спроможностей дуг розрізу складають пропускну спроможність (R, ) розрізу, тобто

(9.4)

Розріз мережі, який має найменшу пропускну спроможність називається мінімальним розрізом.

Приклад. Розглянемо мережу, наведену на рис.9.1

Рис. 9.1 Граф мережі з одним витіком s та одним стоком t.

Для цієї мережі існує 7 розрізів. Наприклад: тоді розріз .

Пропускна спроможність .

Мінімальний розріз

Властивість розрізу: розглядаємо довільний розріз (R, ). Який би шлях з S у t ми не розглядали, хоча б одна його дуга входить у даний розріз (R, ), тому що S і t належать різним множинам R і . Тобто якщо видалити всі дуги якого або розрізу, то в мережі не залишиться шляху, що веде з S до t, тобто будь-який розріз блокує всі шляхи з S у t. В зв’язку з тим що результат пропускної спроможності колій не може бути вище пропускної спроможності будь-якої його дуги, тому сумарний потік V, що тече з S у t по всіх можливих коліям, не може бути вище пропускної спроможності будь-якого розрізу мережі.

(9.5)

Тобто якщо знайти такий потік X*(і, j), що його величина V* дорівнює пропускної спроможності деякого розрізу , то цей потік буде максимальним, а – розріз з мінімальною пропускною спроможністю.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Інші властивості та різновиди графів	\|	Теорема про максимальний потік і мінімальний розріз теорема (Форда – Фолкерсона)

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.02 сек.