
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Приклад.
Розв’язок гри в змішаних стратегіях

 – нижня ціна гри
– нижня ціна гри
 – верхня ціна гри
– верхня ціна гри
Сідловкої точки немає, тому що  . Шукаємо розв’язок гри в змішаних стратегіях.
. Шукаємо розв’язок гри в змішаних стратегіях.






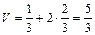 . Аналогічно
. Аналогічно  .
.
4. Розв’язок гри може бути отриманий геометрично (за допомогою графіків)




 називається нижньою межею виграшу.
називається нижньою межею виграшу.
Верхня точка К  визначає розв’язок гри ціну значення гри та ймовірностей.
визначає розв’язок гри ціну значення гри та ймовірностей.



Аналогічно може бути геометрично вирішена гра з матрицею 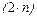 . Результат розв’язання: ціна гри
. Результат розв’язання: ціна гри  ; імовірності
; імовірності  й
й  і вектор
і вектор  , причому всі координати
, причому всі координати  дорівнюють нулю, крім двох.
дорівнюють нулю, крім двох.
Стратегії, що відповідають  називають активними стратегіями.
називають активними стратегіями.
Аналогічно можна геометрично розв’язати гру з матрицею . Геометричний метод може бути використаний тільки для знаходження активних стратегій гравців. Для квадратної матриці другого порядку, що залишилася, розв’язок може бути знайдений аналітично.
. Геометричний метод може бути використаний тільки для знаходження активних стратегій гравців. Для квадратної матриці другого порядку, що залишилася, розв’язок може бути знайдений аналітично.
Контрольні питання
1. Як визначаються нижня і верхня ціни гри?
2. Які стратегії гравців називаються максимінною і мінімаксною?
3. Що називається розв’язанням гри в змішаних стратегіях?
4. Як вирішити гру аналітично у випадку квадратної матриці другого порядку?
5. Як геометрично одержати розв’язок гри в змішаних стратегіях?
Лекція 12
Зведення матричної гри до задачі лінійного
програмування
1. Рівняння і нерівності моделі
2. Вибір заміни змінних, перехід до задачі лінійного програмування
3. Постановка двоїстої задачі
4. Приклад військово-тактичної гри
1. Постановка задачі.
Два гравці:  і
і  . Гра скінченна, маємо
. Гра скінченна, маємо 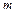 стратегій гравця
стратегій гравця  і n стратегій гравця
і n стратегій гравця  . Задано матрицю гри
. Задано матрицю гри  ,
, 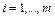 ;
;  ; елементи якої є можливими виграшами гравця
; елементи якої є можливими виграшами гравця  .
.
Припустимо, що матриця не має сідловкої точки, значить  . Гра розв’язується в змішаних стратегіях. Вектори ймовірностей
. Гра розв’язується в змішаних стратегіях. Вектори ймовірностей  і
і  .
.
 - значення гри.
- значення гри. 
При правильній грі гарантійний виграш першого гравця:
 
| (12.1) |
Для другого гравця:
 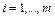
| (12.2) |
Ці нерівності доповнюються умовами:
 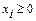 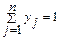 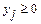
| (12.3) |
2.Припустимо, що  . Введемо нову змінну:
. Введемо нову змінну:
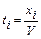
Результат:

| (12.4) |
 
| (12.5) |
Треба ввести цільову функцію для одержання задачі лінійного програмування.
Цільова функція:

| (12.6) |
Задачу можна розв’язати симплекс-методом.
У результаті знайдемо вектор  і
і  .
.
Одержуємо:
  , , 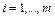
| (12.7) |
Для  виходить двоїста задача.
виходить двоїста задача.

Цільова функція: 
| (12.8) |
Система обмежень:  , ,
| (12.9) |
де  ;
; 

| (12.10) |
Задача (12.8) – (12.10) є двоїстою для задачі (12.4) – (12.6) і  .
.
Оптимальний план задачі: 
 
| (12.11) |
Якщо умова  не виконана, необхідно зробити зміщення до області позитивних виграшів. Для цього до кожного елемента матриці
не виконана, необхідно зробити зміщення до області позитивних виграшів. Для цього до кожного елемента матриці  необхідно додати одне і те ж додатне число.
необхідно додати одне і те ж додатне число.
 .
.
 знаходиться тим же самим способом.
знаходиться тим же самим способом.
Значення гри вийде збільшеним на число  :
:
 .
.
Після закінчення розв’язання знаходимо  і
і  ;
; 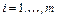 .
.
4. Приклад військово-тактичної гри.
Дві воюючі армії ведуть боротьбу за 2 пункти. Перша армія складається з 4-х полків, друга армія має 3 полки. Армія, що посилає більше полків на той чи інший населений пункт займає його і знищує всі спрямовані на цей пункт сили супротивника. Відповідний гравець одержує одиницю за зайнятий пункт і по одиниці за кожен знищений полк супротивника. У разі рівності сил, спрямованих у деякий пункт, очки не виграються.
Мета гри: розподілити сили так, щоб одержати максимальний загальний виграш.
Стратегія кожного гравця буде визначатися парою чисел  .
.
 – кількість військ, посланих на I пункт,
– кількість військ, посланих на I пункт,  – на II пункт.
– на II пункт.
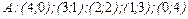 – стратегії першого гравця
– стратегії першого гравця 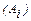 .
.
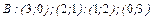 – стратегії другого гравця
– стратегії другого гравця  .
.
Матриця гри
| (3;0) | (2;1) | (1;2) | (0;3) | |
| (4;0) | ||||
| (3;1) | -1 | |||
| (2;2) | -2 | -2 | ||
| (1;3) | -1 | |||
| (0;4) |



 ;
; 

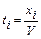
Цільова функція: 
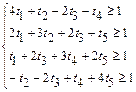

Читайте також:
- Наприклад.
- Наприклад.
- Наприклад.
- Практичний приклад. Екстраверт і інтроверт
- Приклад.
- Приклад.
- Приклад.
- Приклад.
- Приклад.
- Приклад.
- Приклад.
- Приклад.
| <== попередня сторінка | | | наступна сторінка ==> |
| Ігри зі змішаними стратегіями | | | Розв’язок |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |