• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Спосіб обертання навколо проекціювальної осі

Сутність методу: площини проекцій П₁ та П₂ залишають нерухомими, а пряму (площину) обертають навколо введеної осі i, яка займає окреме положення відносно П₁ або П₂ (рис. 58).

Символьні f₂¢ ^ X₁₂, σ₁¢¢úú ‌ Х₁₂,

позначення: σ (DABC) ^ П₁, σ (DABC) úú П₂.

σ ^ П₂ = β.

Рисунок 58 - Надання площині DABC проекціювального та положення рівня

Задача.Прямій АВ загального положення надайте проекціювальне положення (рис. 59).

Задачу розв’язують в два етапи. На першому етапі відносно осі i (i^П₁) пряму повертають до положення, коли вона паралельна фронтальній площині проекцій (А¢В¢ úú П₂). На другому етапі вводять нову вісь i¢ (i^ П₂), відносно якої пряму А¢¢В¢¢ повертають перпендикулярно до П₁ (А¢¢В¢¢ ^П₁).

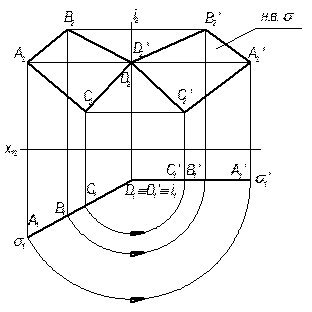
Задача. Визначте натуральну величину чотирикутника АВСD (рис. 60).

Через одну із точок (т. D) чотирикутника проводимо вісь i (i^П₁). Слід-проекцію площини s₁ (A₁B₁C₁D₁) повертаємо до положення, паралельного фронтальній площині проекції (s₁ úú X₁₂). На П₂ отримуємо натуральну величину (A¢B¢C¢D¢) чотирикутника ABCD. Периметр плоскої фігури визначається як сума його сторін.

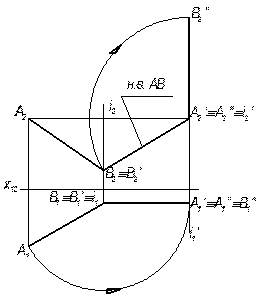
Рисунок 59 – Перетворення прямої загального положення в проекціювальне

p=A₂¢B₂¢+B₂¢D₂¢+D₂¢C₂¢+C₂¢+C₂¢A₂¢

Рисунок 60 – Визначення периметра плоскої фігури

Читайте також:

1. I спосіб.
2. Ne і ne – поточне значення потужності і частоти обертання колінчастого вала.
3. V. Антропогенне забруднення навколоземного простору.
4. Адміністративно-правовий спосіб захисту прав
5. Адміністративно-правовий спосіб захисту прав
6. Алгебраїчний спосіб визначення точки беззбитковості
7. Алгоритм визначення проекцій точок на поверхнях обертання
8. Аналітичний спосіб визначення рівнодійної
9. Аналогія - спосіб отримання знань про предмети та явища на основі їхньої подібності з іншими.
10. Аналогія величин і рівнянь поступального і обертального руху. Кінетична енергія обертання тіла
11. Атракція як спосіб викликати довіру до реклами
12. Бюджетний устрійпоказує, в який спосіб побудована бюджетна система. Іншими словами,він відображає організацію вертикальної структури бюджету держави за рівнями влади.

Переглядів: 1486