• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

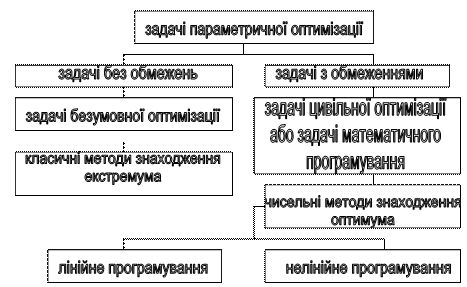
Використання задач параметричної оптимізації

Задачі параметричної оптимізації поділяються на :

- задачі без обмежень;

- задачі з обмеженням на параметр;

Перші задачі називають задачами безумовної оптимізації , а другі – задачами математичного програмування ( задачами умовної оптимізації).

Для розв’язку перших задач є загально відомі методи , одним із яких є метод диференціювання цільової функції, який викладено у математичному аналізі

Методи розв’язку задач умовної оптимізації розроблені поки-що недостатньо , тому у кожному випадку використовуються чисельні методи розв’язку цих задач з використанням ОМ . При умові оптимізації крім цивільної функції ще є і ряд обмежень на шукані параметри . Обмеження можуть бути прямими або функціональними у вигляді рівностей чи нерівностей

Задача є оптимізаційною тоді , коли число рівностей (рівнянь) менше за число невідомих. Такі задачі мають безкінечну множину рішень і для вибору одного з них ,тоб-то оптимального рішення необхідно сформулювати цільову функцію (критерій оптимальності).

Лінійне програмування

За допомогою лінійного програмування можна розв’язувати різні задачі комплексної механізації.

Наприклад :

- здійснювати оптимальну загрузку транспортних засобів ;

- визначити область оптимального використання машин;

- призначати комплекти машин на окремі об’єкти і ділянки будівництва.

До лінійного програмування відноситься такий клас задач у яких і цільова функція і обмеження включають невідомі чи шукані параметри у першій степені. Розв’язок таких задач методом лінійної алгебри неможливий, неможна їх розв’язувати і методом диференціювання .

Як правило вони вирішуються чисельними методами. При двох невідомих розв’язок задачі у лінійного програмування можна представити графічно .

Відомо ,що якщо безперервну функцію двох змінних зобразити в одній площині , то Ії можна охарактеризувати лініями рівня функції чи постійними значеннями функції.

Як приклад розглянемо таку лінійну функцію двох змінних із слідуючими обмеженнями.

F( Х1,Х2)=2Х₁+Х₂

Х₁≥( 0 ); Х₂≥0 Х₁+Х₂≤1

Обмеження дозволяють виділити область допустимих розв´язань , для чого

Х₁+Х₂=1 якщо Х₂=0 ; то Х₁=1

якщо Х₁=0 ; то Х₂=1

Для функцій ,що розглядається , потрібно знайти значення змінних Х₁, Х₂ при яких функція буде досягати максимального значення.

Для цього нанесемо на графік лінії постійних значень функції; для чого

Х₁+Х₂=1 - постійне значення функції

При Х₂=0; Х₁=0,5

Х₁=0; Х₂=1

2Х₁+Х₂

При Х₂=0; Х₁=1

Х₁=0; Х₂=2

Максимального значення функція буде досягати у точці , де трикутник буде торкатися найбільшого рівня. Такою точкою є точка В, В(Х₁=1 , Х₂=0).

Тільки в цій точці отримуємо f_max=2

Оптичним рішенням ЗЛП є координати однієї з вершин ОДР

Для задач лінійного програмування оптимальне значення функції , як правило , знаходяться на межі допустимої області .

Наприклад :

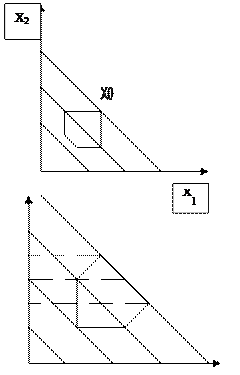
Математична модель задачі лінійного програмування має наступні види:

Цільова функція F=у= Ci Xi

Обмеження :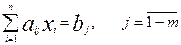

ι     γ			...		n	bγ
m						bm
	С1	С2			Cn

і – номер невідомого;

n – число невідомих даної задачі;

j – номер обмеження;

m – число обмежень.

В задачі повинно бути : n > m;

Х_{ι –} і-тий невідомий параметр;

а_іj – коефіцієнт при невідомих у обмеженнях;

С_ι – коефіцієнт при невідомих у цільовій функції;

в_ι – праві частини обмежень.

Читайте також:

1. I. Застосування похідної та інтеграла до роз’язування задач елементарної математики.
2. XIII. Використання амортизаційних відрахувань
3. А) Задачі, що розкривають зміст дій
4. А. Розрахунки з використанням дистанційного банкінгу.
5. АВТОМАТИЗАЦІЯ РОЗВ’ЯЗУВАННЯ КОМПЛЕКСУ ЗАДАЧ З ОБЛІКУ ОСНОВНИХ ЗАСОБІВ ТА НЕМАТЕРІАЛЬНИХ АКТИВІВ
6. АЕРОЗОЛІ ТА ЇХ ВИКОРИСТАННЯ
7. Актуальні смуги гідрологічних об’єктів та їх використання
8. Алгоритм розв’язання задачі
9. Алгоритм розв’язання задачі
10. Алгоритм розв’язання розподільної задачі
11. Алгоритм розв’язування задачі
12. Алгоритм розв’язування задачі

Переглядів: 1466