
МАРК РЕГНЕРУС ДОСЛІДЖЕННЯ: Наскільки відрізняються діти, які виросли в одностатевих союзах
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
Контакти
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Прийняття рішень в умовах активної протидії
економічного середовища (конфліктні ситуації)
Розглянемо методи прийняття рішень в умовах ризику, пов'язаного з активною протидією зовнішнього середовища, наприклад, конкурентів, коли зіштовхуються інтереси кількох виробників (продавців).
Для цього будемо використовувати методи теорії ігор, які розроблялися для вибору оптимального алгоритму поведінки в азартних іграх. У даний час математичний апарат теорії ігор широко використовується для аналізу різних конфліктних ситуацій.
Розглянемо деякі елементи формалізації конфліктних ситуацій.
У табл. 4.7 наведена математична модель конфліктної ситуації (гра) у вигляді матриці виграшів.
Модель конфліктної ситуації
| Стратегії гравця А | Стратегії гравця В | ||
| B1 | Bi | Bn | |
| А1 | q11 | q1j | q1n |
| Аj | qi1 | qij | qin |
| Аm | qm1 | qmj | qnm |
Величина qij відповідає виграшеві гравця А при власній стратегії поведінки Аj і стратегії супротивника Вj.
У табл.4.7 представлена матриця парної гри, оскільки розглядаються антагоністичні стратегії поведінки двох гравців, наприклад, виробників аналогічної продукції.
Гра є конечною, оскільки представлено конечну кількість стратегій (слід зазначити, що далеко не кожну гру можна звести до конечної кількості стратегій).
Оптимальною вважається така стратегія гравця, яка забезпечує йому максимальний виграш.
Якщо сума виграшів гравців дорівнює нулю, то така гра вважається грою з нульовою сумою.
У цьому випадкувиграш одного можливий тільки за рахунок програшу іншого.
Нижня межагри визначається з умови
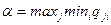
Це означає, щояку би стратегію не використовував гравець В, гравець А гарантує собі виграш не менше ніж α.
Верхня межа гривизначається з умови
Читайте також:
- III. Сприйняття й засвоєння учнями навчального матеріалу
- IV. Прийняття рішень у полі четвертої інформаційної ситуації
- IV. Сприйняття та усвідомлення навчального матеріалу
- V. Прийняття рішень у полі п’ятої інформаційної ситуації
- VI. Прийняття рішень у полі шостої інформаційної ситуації
- Актуальність і завдання курсу безпека життєдіяльності. 1.1. Проблема безпеки людини в сучасних умовах.
- Алгоритм прийняття рішення при прийманні сигналів з випадковою початковою фазою
- Аналіз альтернативних рішень
- Аналіз для прийняття рішень стосовно залучення інвестицій
- Аналіз та оцінка інвестування в умовах ризику. Якісні та кількісні методи оцінювання проектних ризиків.
- Аналітична робота в умовах кризи.
- Аналітичні методи та інструменти підтримки прийняття управлінських рішень.
| <== попередня сторінка | | | наступна сторінка ==> |
| Прийняття рішень в умовах неповної поінформованості про характеристики | | | Приклад . |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |