• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Сутність і методи лінійного програмування

Лінійне програмування використовує математичний інструментарій, який базується на теорії і методах вирішення задач про екстремуми лінійних функцій, що задаються системами лінійних рівнянь. Термін «програмування» визначається як «планування».

Найбільш універсальним методом є диференціальний алгоритм, логічно випливає з диференціального алгоритму загальної задачі математичного програмування. Диференціальний алгоритм, як і широко відомий симплекс-метод, дозволяє вирішувати будь-які задачі лінійного програмування. однак для деяких класів задач лінійного програмування доцільно використовувати більш прості методи. Так, для вирішення задач із кількістю змінних, рівною двом, використовують графічний метод, що відзначається простотою і наочністю, але потребує графічних побудов. Для вирішення задач лінійного програмування, відомих як транспортні, використовують метод потенціалів.

Методичною основою обчислювальних процедур будь-якого методу є принцип аналізу і послідовного поліпшення деякого початкового плану розподілу і використання ресурсів. План поліпшують доти, поки не буде знайдений найкращий (оптимальний) варіант. Іншими словами, спочатку складається деякий початковий план, що аналізується за конкретними строго розробленими правилами. На підставі аналізу визначаються можливість і напрямок поліпшення початкового варіанта плану. Потім обчислюється новий план, що піддається такому ж аналізу і подальшому поліпшенню, тобто наближенню до оптимуму. Обчислювальний процес продовжується доти, поки аналіз не покаже неможливість дальшого поліпшення.

Слід декілька слів сказати про симплекс-метод. Він використовується до вирішення будь-якої задачі лінійного програмування. Сутність симплекс-методу полягає в тому, що, відправляючись з деякої довільної вершини багатокутника обмежень, переходять до обчислення тільки такої вершини, в якій значення лінійної форми буде більше, ніж в попередній. Решта варіантів не обчислюється. Тоді при кінцевому порівняно малому числі кроків може бути знайдений оптимальний план. Таким чином, проводиться впорядкований перебір вершин, при якому відбувається постійне збільшення лінійної форми. В цьому аспекті симплексний метод називається також методом послідовного поліпшення плану.

Вирішення задач лінійного програмування симплекс-методом полягає:

- по-перше, в розробці базового рішення на оптимальність. Якщо воно оптимальне, то задача вирішена, в іншому випадку виконують другий етап;

- по-друге, визначаються вектор , який повинен бути введений в базис, і вектор , який повинен бути виключений з нього, тобто виходить новий базисний план з великим значенням лінійної форми. Щоб знайти вектори і , заміна яких забезпечує найбільше зростання лінійної форми, виразимо всі вектори, що не входять в базис, через базисні вектори

(3.1)

де a_ij - проекції вектора 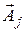на вектор . Запишемо систему обмежень у векторній формі в наступному вигляді:

(3.1)

Оскільки то

(3.2)

Співвідношення (3.2) дає рішення тільки у тому випадку, коли коефіцієнти при векторах і нового базису будуть ненегативними, тобто

і (3.3)

Відповідне нове значення лінійної форми прийме вигляд

(3.4)

Позначимо

(3.5)

Тоді значення лінійної форми в новій вершині багатокутника рішення можна знайти з рівняння

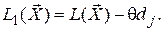(3.6)

Величину d_j називають оцінкою плану. В симплексному методі параметри d_j відіграють важливу роль: їх знаки дозволяють визначити, чи є опорний план оптимальним. Якщо dj 0 для всіх j, то даний опорний план є оптимальним, оскільки на підставі (3.6) і зважаючи на q ³ 0 перехід до будь-якої нової вершини веде до убування лінійної форми. Якщо опорний план неоптимальний, то можливі два випадки:

1. Є хоча б один індекс j = k для якого d_k < 0 і всі відповідні компоненти В цьому випадку лінійна форма не обмежена зверху і задача нерозв'язна.

2. Для деяких j d_j < 0 і для кожного такого j, принаймні, одна з проекцій a_ij >0. Тоді при переході до наступної вершини лінійна форма зростає і план поліпшується. Для найшвидшого зростання L необхідно в базис включити той вектор , для якого оцінка d_k < 0 і максимальна по модулю, а вектор , для якого значення позитивно і мінімально, виключити.

Також при лінійному програмуванні використовують методи еліпсоїдів, метод внутрішніх крапок, методи логарифмічних бар'єрних функцій нелінійного програмування. В цих методах вирішення задач лінійного програмування здійснюється шляхом пошуку уздовж траєкторій в просторі змінних задачі, що не проходять через вершини багатокутника.

Читайте також:

1. B. Тип, структура, зміст уроку і методика його проведення.
2. Demo 11: Access Methods (методи доступу)
3. I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
4. II. МЕТОДИЧНІ ВКАЗІВКИ
5. II. УЧЕБНЫЕ И МЕТОДИЧЕСКИЕ ПОСОБИЯ, ПРАКТИКУМЫ
6. IV. КЕРІВНИЦТВО, КОНТРОЛЬ І НАДАННЯ ОРГАНІЗАЦІЙНО-МЕТОДИЧНОЇ ДОПОМОГИ ПРАКТИКАНТАМ.
7. IV. Учебно-методические рекомендации
8. IV. Электронное учебно-методическое обеспечение дисциплины.
9. T. Сутність, етіологія та патогенез порушень опорно-рухової системи
10. V. ІНДИВІДУАЛЬНІ ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ ТА МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ДО ЇХ ВИКОНАННЯ
11. V. Обов'язки методиста кафедри педагогіки
12. VIІ. Короткі методичні вказівки до роботи студентів на практичному занятті

Переглядів: 2851