• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Особливості задач лінійного програмування та практичні аспекти їх вирішення

Задачам лінійного програмування властиві наступні особливості:

1. Цільова функція є зваженою лінійною сумою від невідомих змінних x_i вигляду:

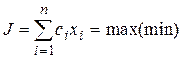_. (3.7)

де c_i – коефіцієнти цільвої функції. Таку цільову функцію часто називають лінійною формою.

2. Обмеження, що накладаються на область можливих рішень, мають вид лінійної рівності або нерівності:

. (3.8)

де a_ij, b_i – значення показників цільової функції, причому величини a_ij, x_i, b_i позитивні.

Розглянемо деякі практичні аспекти вирішення задач лінійного програмування.

Приклад. Фірма виробляє дві моделі А і В збірних книжкових полиць. Їх виробництво обмежено наявністю сировини (високоякісних дощок) і часом машинної обробки. Для кожного виробу моделі А потрібен 3 м² дощок, а для моделі В - 4 м². Фірма може одержувати від своїх постачальників до 1700 м² дощок в тиждень. Для кожного виробу моделі А потрібно 12 хв. машинного часу, а для виробу моделі В - 30 хв. В тиждень можна використовувати 160 годин машинного часу. Скільки виробів кожної моделі слід випускати фірмі в тиждень, якщо кожний вироб моделі А приносить 2 грн. прибутку, а кожний виріб моделі В - 4 грн. прибутку?

Вирішення

Побудова математичної моделі.

Хай x₁ - кількість випущених за тиждень полиць моделі А, а x₂ - кількість випущених полиць моделі В.

Тоді: 3x₁ - кількість дощок, що необхідно на тиждень для виготовлення полиць моделі А

4x₂- кількість дощок, що необхідно на тиждень для виготовлення полиць моделі В

3x₁ + 4x₂- кількість дощок що вимагаються на тиждень для виготовлення книжкових полиць двох моделей, а за умовами задачі це число не повинно перевищувати 1700 м², отже, одержуємо перше обмеження:

3x₁+ 4x₂<=1700 (1)

Знайдемо обмеження на використання машинного часу.

12 хв. складають 0,2 години, а 30 хв. - 0,5 години, таким чином:

0,2x₁ - кількість часу, що вимагається на тиждень для виробництва полиць моделі А;

0,5x₂ - кількість часу, що вимагається на тиждень для виробництва полиць моделі В;

0,2x₁ + 0,5x₂ - кількість часу, що необхідно на тиждень для виробництва двох моделей, а по умові задачі це число не повинно перевищувати 160 годин, отже, одержуємо друге обмеження:

0,2x₁ + 0,5x₂<=160 або 2x₁ + 5x₂<=1600 (2)

Крім того, оскільки x₁ і x₂ виражають щотижневий обсяг виробів, що випускаються, то вони не можуть бути негативними, тобто

x₁>=0, x₂>=0 (3)

Ця задача полягає в тому, щоб знайти такі значення x₁ і x₂, при яких щотижневий прибуток буде максимальним. Складемо вираз для щотижневого прибутку:

2x₁ - щотижневий прибуток, який одержаний від продажу полиць моделі А.

4x₂ - щотижневий прибуток, який одержаний від продажу полиць моделі В

Тоді F=2x₁ + 4x₂ - щотижневий прибуток, який повинен бути максимальним. Таким чином, маємо наступну математичну модель для даної задачі.

F=2x₁ + 4x₂->max

Отримана модель є задачею лінійного програмування. Функція F - це цільова функція, вона є лінійною функцією своїх змінних(x₁ і x₂). Обмеження на ці змінні (1) і (2) теж є лінійними. Виконана умова позитивності для змінних x₁ і x₂.

Необхідно знайти значення змінних x₁ і x₂, при яких дана функція F приймає максимальне значення, при дотриманні обмежень, що накладаються на ці змінні.

Рішення, що задовольняють системі обмежень і вимогою позитивності, є допустимими, а рішення, що задовольняють одночасно і вимогою мінімізації (максимізації) функції в цілому є оптимальними.

Читайте також:

1. I. ЗАДАЧИ ДЛЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ И САМОСТОЯТЕЛЬНЫХ РАБОТ
2. I. Застосування похідної та інтеграла до роз’язування задач елементарної математики.
3. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
4. II. Практичні завдання
5. II. Практичні завдання.
6. III. Інформаційне забезпечення задачі
7. IIІ. Інформаційне забезпечення задачі
8. IV. Алгоритм вирішення задачі
9. IV. Алгоритм розв’язання задачі
10. IV. Алгоритм розв’язання задачі
11. IV. Алгоритм розв’язання задачі
12. IV. ДІЯ ЦЬОГО ЗАКОНУ І ОСОБЛИВОСТІ ЙОГО ЗАСТОСУВАННЯ

Переглядів: 679