
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Транспортна задача. Математичне формулювання і алгоритм вирішення
В аспекті вирішення задач лінійного програмування розглянемо математичне формулювання і алгоритм розв’язання транспортної задачі.
Змістовна постановка задачі: Однорідний продукт, зосереджений у m пунктах відправлення в кількостях а1, а2, ... аm одиниць відповідно, необхідно доставити в кожний із n пунктів призначення в кількості b1, b2, ... bn одиниць відповідно. Вартість (відстань) перевезення одиниці продукту з i-го пункту відправлення j-й пункт призначення дорівнює сij і відома для кожного маршруту. Нехай xij - кількість продукту, перевезеного з і-ro пункту відправлення в j-й пункт призначення. Задача полягає у визначенні таких розмірів xij для всіх маршрутів, при яких сумарна вартість (відстань) перевезень була б мінімальною.
Математична модель задачі:
Позначимо:
сij - тарифи (вартість, час, відстань) перевезення одиниці вантажу з i-го пункту відправлення в j-й пункт призначення;
ai - запаси вантажу в i-му пункті відправлення;
bі — потреба у вантажі в j-му пункті призначення;
xij - кількість одиниць вантажу, перевезеного з 1-го пункту відправлення в j-й пункт призначення.
Тоді математична модель транспортної задачі про планування перевезень має такий вигляд:
m n
y=∑∑cijxij→min; (3.9)
i=1 j=1 xijÎΩ
m ____
Ω: fj=∑xij=bi, j=1,n; (3.10)
i=1
n ____
fn+i=∑xij=ai, i=1,m; (3.11)
j=1 _______ _______
xij≥0; i=1,m; i=1,m. (3.12)
Тут (3.9) - цільова функція, що визначає вартість перевезень усього вантажу. Саме екстремальне (мінімальне) значення цієї функції необхідно знайти в задачі. Причому значення змінних хij, при яких цільова функція досягає свого мінімуму, повинні належати області припустимих рішень Ω.
Вирази (3.10) - (3.12) визначають область припустимих рішень Ω. При цьому вираз (3.10) відбиває потреби у вантажі в пунктах призначення, вираз (3.11) визначає запаси вантажів у пунктах відправлення, а вираз (3.12) відокремлює негативну область значень хij, в яку дані змінні не можуть потрапляти за своїм фізичним змістом.
Вирази (3.10)-(3.12) називаються обмеженнями задачі лінійного програмування. Вирішення задачі (частковий набір значень змінних xi) називається припустимим, якщо воно одночасно задовольняє всім 1 обмеженням задачі. Вирішення задачі називається оптимальним, якщо воно забезпечує оптимум (у даному випадку мінімум) функції цілі.
Вважатимемо, що функції y,f1,f2, ... ,fn - неперервні лінійні функції, задані на невід'ємному ортанті евклідового простору Rn. Дані функції мають місце, коли перевезений вантаж є рідиною, сипкою речовиною, дрібними заготівлями або дрібною неспакованою продукцією. Такий вантаж характеризується параметрами, що являють собою вагу, довжину (погонні метри), площу (квадратні метри), об'єм і т.п.
Якщо загальна потреба у вантажі в пунктах призначення дорівнює запасу вантажу в пунктах відправлення, тобто
m n
∑ai=∑bj , (3.13)
i=1 j=1
то модель такої транспортної задачі називається закритою. У противному випадку - відкритою.
Теорема 1.1. Для можливості розв'язання транспортної задачі необхідно і достатньо, щоб запаси вантажу в пунктах відправлення були рівні потребам у вантажі в пунктах призначення, тобто щоб виконувалася рівність (3.13).
У випадку перевищення запасу над потребою, тобто 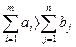 вводиться фіктивний (n+1)-й пункт призначення з потребою
вводиться фіктивний (n+1)-й пункт призначення з потребою  . При цьому відповідні тарифи вважаються рівними нулю:ci,n+1=0 (i=1,m) .Така задача буде вже транспортною задачею, для якої умова (3.13) виконується.
. При цьому відповідні тарифи вважаються рівними нулю:ci,n+1=0 (i=1,m) .Така задача буде вже транспортною задачею, для якої умова (3.13) виконується.
Аналогічно, якщо  , вводиться фіктивний (m+1)-й пункт відправлення з запасом вантажу
, вводиться фіктивний (m+1)-й пункт відправлення з запасом вантажу  .При цьому відповідні тарифи вважаються рівними нулю: cm+1,j=0 (j=1,n).Така задача буде вже транспортною задачею, для якої умова (3.13) виконується.
.При цьому відповідні тарифи вважаються рівними нулю: cm+1,j=0 (j=1,n).Така задача буде вже транспортною задачею, для якої умова (3.13) виконується.
Далі будемо розглядати закриту модель транспортної задачі. Якщо ж модель конкретної задачі є відкритою, то, виходячи зі сказаного вище, її необхідно перетворити так, щоб виконувалася рівність (3.13).
У відкритій моделі область припустимих значень (за інших рівних умов) значно ширше, тому цільова функція досягає кращих значень або, принаймні, не гірше.
Особливості вирішення закритої транспортної задачі:
Визначення 1.1. Усяке невід'ємне рішення систем лінійних рівнянь (3.10) і (311) , що обумовлене матрицею X={xij], i=1,m, j=1,n, називається планом транспортної задачі.
Визначення 1.2. План X* =[x*ij], i=1,m, j=1,n, при якому функція (3.9) приймає своє мінімальне значення, називається оптимальним планом транспортної задачі.
Число перемінних xijy транспортній задачі з m пунктами відправлення і n пунктами призначення дорівнює mn, а число рівнянь у системах (3.10) і (3.11) дорівнює m+n. Оскільки передбачається, що виконується умова (3.13), то число лінійно незалежних рівнянь дорівнює m+n-1. Отже, опорний план транспортної задачі може мати не більше m+n-1 відмінних від нуля невідомих.
Визначення 1.3. План X* =[x*ij], i=1,m, j=1,n є опорним невиродженим, якщо в ньому кількість відмінних від нуля компонентів у точності дорівнює m+n-1, а якщо менше - то виродженим.
Для визначення опорного плану існує декілька методів. Один з них - метод північно-західного кута - буде розглянутий нижче.
Як і для всякої задачі лінійного програмування, оптимальним план транспортної задачі є також опорним планом. Для визначення оптимального плану транспортної задачі можна використовувати диференціальний алгоритм, симплекс-метод та інші універсальні методи. Однака через виняткову практичну важливість цієї задачі і специфіку її обмежень (кожна невідома входить лише в два рівняння систем (3.10) і (3.11), а коефіцієнти при невідомих дорівнюють одиниці) для визначення оптимального плану транспортної задачі розроблені спеціальні методи. Один з них - метод потенціалів - розглядається в даному курсі.
За звичаєм вихідні дані транспортної задачі записують у вигляді табл.3.1.
Таблиця 3.1. Вихідні дані транспортної завдання
| Пункти відправлення | Запаси | Пункти призначення | |||||
| … | j | … | n | ||||
| Потреби | |||||||
| b1 | b2 | … | b1 | … | bn | ||
| a1 | c11 x11 | c12 x12 | … | c1j x1j | … | c1n x1n | |
| a2 | c21 x21 | c22 x22 | … | c2j x2j | … | c2n x2n | |
| … | … | … | … | … | … | … | … |
| i | ai | ci1 xi1 | ci2 xi2 | … | cij xij | … | cin xin |
| … | … | … | … | … | … | … | … |
| m | am | cm1 xm1 | cm2 xm2 | … | cmj xmj | … | cmn xmn |
Визначення початкового опорного плану транспортної задачі: Вирішення транспортної задачі починають із знаходження будь-якого опорного плану. Для цього розроблені специфічні методи. Один з них одержав у літературі назву "метод північно-західного кута". Іноді його називають також "діагональним методом", "методом перехідних приступів" і т. ін.
Сутність методу полягає в тому, що опорний план знаходять за m+n-1 кроками, на кожному з яких у таблиці транспортної задачі заповнюють одну клітку. Заповнення однієї клітки забезпечує цілком або задоволення потреби у вантажі одного з пунктів призначення (відповідно до того, в стовпці якого знаходиться клітка), або вивіз вантажу з одного з пунктів відправлення (відповідно з того, в рядку якого знаходиться клітка).
Заповнення таблиці слід починати з лівого верхнього квадрата (північно-західного кута). З позиції цього квадрата порівнюють запас вантажу в першому пункті відправлення з потребою першого пункту призначення. Вибирають менший розмір і записують у даний квадрат, який з цього моменту стає "зайнятим". Якщо в клітку записується потреба пункту призначення, то з подальшого розгляду виключають відповідний стовпець таблиці і переходять у ліву сусідню клітку. Якщо в клітку записується запас пункту відправлення, то з подальшого розгляду виключають відповідний рядок таблиці і переходять у сусідню клітку, що знаходиться нижче заповненої.
У новій клітці для частини таблиці, що залишилася, повторюють процедуру першого кроку з урахуванням зміни запасу вантажу одного з І відправників або потреби у вантажі одного з одержувачів у результаті попереднього кроку.
Після m+n-2 описаних вище кроків одержують задачу з одним пунктом відправлення і одним пунктом призначення. При цьому залишається вільною тільки одна клітка, а запаси пункту відправлення дорівнюватимуть потребам пункту призначення. Заповнення цієї клітки, тобто здійснення (m+n-1)-го кроку приводить до шуканого опорного плану.
Слід зауважити, що в процесі використання методу північно-західного кута може трапитися, що потреби у вантажі чергового пункту призначення рівні запасам чергового пункту відправлення. У цьому випадку з подальшого розгляду виключають або стовпець, або рядок, тобто тільки що-небудь одне. Таким чином, запаси відповідного пункту відправлення, або потребу відповідного пункт призначення вважають рівними нулю. Цей нуль записують у чергову клітку, яка заповнюється [61].
Зазначені вище умови гарантують одержання m+n-1 зайнятих кліток, у яких знаходяться компоненти опорного плану.
Опорний план перевезень повинен відповідати таким вимогам:
по-перше, кількість зайнятих маршрутів (кліток) повинно бути на одиницю менше суми числа постачальників т і числа споживачів п, тобто повинна дорівнювати значенню m+n-1;
по-друге, не повинно бути жодного зайнятого маршруту (клітки), що опинився: б єдиним і в рядку, і в стовпці таблиці.
Визначення оптимального опорного плану транспортної задачі:
Для відзначення оптимального плану транспортної задачі розроблено декілька методів. Найбільш часто використовується метод потенціалів. Метод припускає, що вже відомий якийсь опорний план. Його можна одержати, наприклад, розглянутим методом північно-західного кута. Вихідний опорний план необхідно перевірити на оптимальність.
Теорема 1.2. Якщо для деякого опорного плану X* =[x*ij], i=1,m, j=1,n транспортної задачі з заданими тарифами перевезень cij існують такі числа αi(i=1,m) i βj(j=1,n), що
βi-αj=cij при xij>0 (3.14)
і βi-αj≤cij при xij=0 (3.15)
для всіх i=1,m і j=1,n, то X* =[x*ij] - оптимальний план.
Визначення 1.4. Числа αi(i=1,m) i βj(j=1,n) називаються потенціалами відповідно пунктів відправлення і пунктів призначення.
Теорема 1.2 дозволяє побудувати алгоритм знаходження рішення транспортної задачі. Він являє собою наступне.
Нехай знайдений опорний план транспортної задачі. Для кожного з пунктів відправлення і призначення визначають потенціали αi(i=1,m) i βj(j=1,n) із системи рівнянь
βi-αj=cij. (3.16)
Тому що число заповнених кліток дорівнює n+m-1, то система (3.16) із n+m невідомими містить n+m-1 рівнянь. Оскільки число невідомих перевищує на одиницю число рівнянь, одне з невідомих потрібно взяти рівним довільному числу, наприклад α1=0, і знайти послідовно із системи (3.16) значення інших невідомих.
Після того, як усі потенціали знайдені, дія кожною з вільних кліток визначають числа αij=βi-αj-cij. Якщо серед чисел αij немає позитивних, то знайдений опорний план є оптимальним. Якщо ж для деякої вільної клітки αij>0, то опорний план , що перевіряється , не є оптимальним, і треба перейти до нового опорного плану. Для цього розглядають усі вільні клітки, для яких αij>0, і вибирають ту, для якої число αij максимальне. Обрану клітку необхідно заповнити.
Заповнюючи обрану клітку, треба змінити обсяги перевезень, записаних у ряді інших зайнятих клітках і зв'язаних з обраною циклом.
Визначення 1.5. Циклом у таблиці транспортної задачі називається замкнута ломана лінія, вершини якої розташовані в зайнятих клітках таблиці, а ланки - уздовж рядків і стовпів, причому в кожній вершині циклу зустрічаються рівно дві ланки, одна з яких знаходиться в рядку, а інша - у стовпці.
Якщо ломана лінія, що складає цикл, перетинається сама із собою, то точка самоперетину не є вершиною.
При правильній побудові опорного плану для будь-якої вільної клітки можна побудувати тільки один цикл. Після того як для обраної вільної клітки він побудований, необхідно перейти до нового опорного плану. Для цього треба перемістити вантажі в межах кліток, що утворюють цикл. Переміщення роблять за такими правилами:
кожній з кліток, пов'язаних циклом з обраною вільною кліткою, і приписують знак "+" або "-", причому вільній клітці - знак плюс, а всім іншим кліткам - по черзі знаки мінус і плюс;
у вільну клітку переносять менше з чисел xij, що знаходяться в мінусових клітках, і одночасно це число додають до відповідних чисел, і що знаходяться "плюсових" клітках, і віднімають із чисел, що знаходяться в "мінусових" клітках. Клітка, що раніше була вільною, стає зайнятою, а "мінусова" клітка, в якій стояло мінімальне число xij, стає вільною.
У результаті зазначених вище переміщень вантажів у межах кліток, пов'язаних циклом з обраною вільною кліткою, визначають новий опорний план транспортної задачі. Число зайнятих кліток залишається рівним n+m-1. Якщо в зайнятих "мінусових" клітках циклу є два і більше однакових мінімальних чисел xij, то звільняють тільки одну з таких кліток, а інші залишають зайнятими з нульовими постачаннями.
Отриманий новий опорний план транспортної задачі перевіряють на оптимальність. Для цього визначають потенціали пунктів відправлення і призначення і знаходять числа αij=βi-αj-cij для всіх вільних кліток. Якщо серед цих чисел не буде позитивних, то це означає, що новий опорний план є оптимальним. Якщо ж є позитивні числа, то І необхідно перейти до нового опорного плану. У результаті ітераційного плану кінцевого числа переходів одержують оптимальний план процесу після задачі.
Таким чином, процес знаходження рішення транспортної задачі методом потенціалів включає наступні етапи:
1-й етап. Знаходять опорний план.
2 й етап. Знаходять потенціали пунктів відправлення; і призначення.
3-й етап. Визначають числа αij для кожної вільної клітки. Якщо серед них немає позитивних, то отримано оптимальний план транспортної задачі, у противному разі переходять до нового опорного плану.
4-й етап. Вибирають серед позитивних чисел αij максимальне, будують для відповідної вільної клітки цикл перерахування і роблять зсув за циклом, одержуючи при цьому новий опорний план. Далі переходять до 2-го етапу.
Розглянемо приклад вирішення транспортної задачі методом потенціалів.
Приклад вирішення транспортної задачі методом потенціалів:
Приклад 1.1. Три заводи, що виготовляють бетоні конструкції, постачаються цементом з чотирьох складів. Попит заводів bj відповідно дорівнює 280, 90 і 180 тис.т/міс. Пропускна здатність складів ai,- відповідно становить 200, 150, 80 і 120 тис.т/міс. Відстані перевезень (у км)
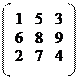 |
із і-го складу на j-й завод подані в матриці C=[cij]=
Потрібно скласти план перевезень цементу зі складів на заводи, що задовольняв би пропускним спроможностям складів і потребам заводу, а сумарний пробіг вантажного транспорту був би мінімальним.
Вирішення
Позначимо через xij - кількість цементу, який щомісяця потрібно доставляти щомісяця на j-го завод з i-го складу. Тоді математична модель задачі має вигляд:
y=x11+5x12+3x13+6x21+8x22+9x23+2x31+7x32+4x33+4x41+x42+11x43→min; (3.17)
xijÎΩ
Ω: x11+x21+x31+x41=280; (3.18)
x12+x22+x32+x42=90; (3.19)
x13+x23+x33+x43=180; (3.20)
x11+x12+x13=200; (3.21)
x21+x22+x23=150; (3.22)
x31+x32+x33=80; (3.23)
x41+x42+x43=120; (3.24)
xij³0. (3.25)
Тут (3.17) - цільова функція, (3.18) - (3.20) - обмеження задачі! що визначають місячні запаси цементу на складах, (3.21) - (3.24) – обмеження задачі, що визначають місячну потребу в цементі на заводах (3.25) - обмеження, що визначає неможливість негативних значень для постачань цементу на заводи.
1-й крок. 1-й етап. Використовуючи метод північно-західного кута, знайдемо опорне рішення транспортної задачі (3.17)- (3.25).
Відповідно до цього методу заповнюємо таблицю, починаючи лівого верхнього квадрата. Порівнюємо запас вантажу в першому пункті відправлення (200 тис.т/міс.) із потребою першого пункту призначення (280 тис.т/міс.). Вибираємо меншу величину (200) і записуємо її в даний квадрат. Оскільки весь запас у першому пункті відправлення вичерпаний, то з подальшого розгляду виключаємо перший рядок і переходимо в сусідню клітку, що знаходиться нижче заповненої. У новій клітці для частини таблиці, що залишилася, повторюємо процедуру заповнення верхньої лівої клітки, але з урахуванням того, що потреба першого пункту призначення зменшилася на 200 тис.т/міс. і стала рівною 80 тис.т/міс. Тобто порівнюємо запас другого пункту відправлення (150 тис.т/міс.) із новою потребою першого пункту призначення (80 тис т/міс). Вибираємо меншу величину(80) і записуємо її в нову клітку Оскільки потреба у вантажі в першому пункті призначення повністю задоволена, то з подальшого розгляду виключаємо перший стовпець і переходимо в сусідню клітку, що знаходиться справа від тільки що заповненої. Для нової верхньої лівої клітки частини таблиці, що залишилася, повторюємо процедуру заповнення з урахуванням зміни запасу в другому пункті відправлення на 50 тис.т/міс. І так доти, поки не буде заповнено m+n-2 кліток.
Остання (m+n-2)-я клітка заповнюється механічно - у неї записується залишкова потреба останнього пункту призначення або залишковий запас останнього пункту відправлення. В умовах задачі це величина 120. Усі проміжні результати по знаходженню початкового опорного плану

Х0 = відображені в табл. 3.2. Ці результати в таблиці виділені напівжирним шрифтом.
Для початкового опорного плану обчислюємо значення цільової функції (3.17):
y0=1х200+6х80+8х70+7х20+4х60+11х120=2940 тис.т/міс.
Це значення буде використано на наступних кроках для контролю просування до оптимуму. Значення цільової функції повинно послідовно зменшуватися з кожним кроком.
Таблиця 3.2. Проміжні результати по знаходженню початкового опорного плану
| Пункт відправ-лення | Запас вантажу | Пункт призначення | Потенціал пункту відправлення ai | ||
| Потреба | |||||
| -5 | |||||
| - 20 | + 60 | -4 | |||
| + | - 120 | -11 | |||
| Потенціал пункту призначення bi |
2-й етап. Знайдений опорний план перевіряємо на оптимальність. У зв'язку з там знаходимо потенціали пунктів відправлення і призначення із системи
b1-a1=1, b2-a2=8, b3-a3=4,
b1-a2=6, b2-a3=7, b3-a4=11.
що містить шість рівнянь із сімома невідомими. Вважаючи a1=0, знаходимо b1=1, a2=-5, b2=3, a3=-4, b3=0, a3=-11. Записуємо знайдені потенціали в табл.3.2.
3-й етап. Для кожної вільної клітки обчислюємо числа αij=βi-αj-cij: α12=-2, α13=-3, α23=-4, α31=3, α41=8, α42=13.
Записуємо знайдені числа у відповідні вільні клітки табл.3.2 і вміщуємо їх у рамочки, щоб відрізняти їх від іншої інформації в таблиці Тому що серед чисел αij є позитивні, то опорний план Х0 не є оптимальним.
4-й етап. Серед позитивних чисел αij вибираємо максимальне: α42=13. Для відповідної вільної клітки будуємо цикл, а саму клітку позначаємо знаком «+». У табл.3.2 зайняті клітки, що складають цикл, виділені сірим фоном. Потім позначаємо знаками «-» і «+» по черзі інші клітки циклу, слідуючи уздовж ломаної лінії циклу.
Найменшим із чисел xij у «мінусових» клітках є x32 (20). Дана клітка стає вільною, а інші клітки циклу змінюють свої значення в такий спосіб: Х42=20, х43=120-20=100, х33=60+20=80.
У результаті зроблених перетворень одержуємо новий опорний план

X1=
При такому опорному плані функція цілі (3.17) стає рівною 2680 тис.т/міс, що менше вихідного значення 2940 тис.т/міс.
На цьому закінчується 1-й крок оптимізації. На наступному кроці процедура 1-го кроку повторюється, але без 1-го етапу.
2-й крок. Аналізуємо новий опорний план (табл.3.3) на оптимальність. Знову знаходимо потенціали пунктів відправлення і пунктів призначення, для чого складаємо таку систему рівнянь:
b1-a1=1, b2-a2=8, b2-a4=1,
b1-a2=6, b3-a3=4, b3-a4=11.
Вважаючи a1=0, знаходимо b1=1, a2=-5, b2=3,a4=2, b3=13, a3=9. Для кожної вільної клітки обчислюємо числа αij: α12=-2, α13=10, α23=9, α31= -10, α32=-13, α41=-5.
Тому що серед чисел αij є позитивні (α13=10, α23=9), то опорний план X1 не є оптимальним.
Таблиця 3.3. Новий опорний план
| Пункт відправ-лення | Запас вантажу | Пункт призначення | Потенціал пункту відправлення ai | ||
| Потреба | |||||
| - 200 | + | ||||
| + 80 | - 70 | -5 | |||
| + 20 | - 100 | ||||
| Потенціал пункту призначення bi |
Серед позитивних чисел αij вибираємо максимальне: α13=10. Для відповідної вільної клітки будуємо цикл, а саму клітку позначає знаком «+». У табл.3.3 зайняті клітки, що складають цикл, виділені рим фоном. Потім позначаємо вузлові клітки циклу по черзі знаками «-» і «+».
Найменшим із чисел xij у «мінусових» клітках є х23 (70). Дана клітка стає вільною, а інші клітки циклу змінюють свої значення в так спосіб: x11=200-70=130, x13=70, х21=80+70=150, x42=20+70=90, x43=100-70=30.
У результаті виконаних перетворень одержуємо новий опори план

Х2=
При такому опорному плані функція (3.17) стає рівною 1980 тис.т/міс, що значно менше попереднього значення 2680 тис.т/міс.
3-й крок. Аналізуємо новий опорний план (табл. 3.4) на оптимальність. Знову знаходимо потенціали пунктів відправлення і пунктів призначення, для чого складаємо наступну систему рівнянь:
b1-a1=1, b1-a2=6, b2-a4=1,
b3-a1=3, b3-a3=4, b3-a4=11.
Вважаючи a1=0, знаходимо b1=1, b3=3, a2=-5, b3=4, a3=0, a4=-8, b2=-7. Для кожної вільної клітки обчислюємо числа αij: α12=-12, α22=-10, α23=-1, α31=-1, α32=-14, α41=5. Оскільки серед чисел αij одне позитивне (α41=5), то опорний план Х2 не є оптимальним.
Таблиця 3.4. Новий опорний план
| Пункт відправ-лення | Запас вантажу | Пункт призначення | Потенціал пункту відправлення ai | ||
| Потреба | |||||
| - 130 | + 70 | ||||
| -5 | |||||
| + | - 30 | -8 | |||
| Потенціал пункту призначення bi | -7 |
Для відповідної вільної клітки (нижньої, лівої) будуємо цикл, а саму клітку позначаємо знаком «+». У табл.3.4 зайняті клітки, що складають цикл, виділені сірим фоном. Потім позначаємо вузлові клітки циклу по черзі знаками «-» і «+». Найменшим із чисел xij у «мінусових» клітках є х43 (30). Дана клітка стає вільною, а інші клітки циклу змінюють свої значення в такий спосіб: x11 =130-30=100, х13 =70+30=100, x14=30.
У результаті зроблених перетворень одержуємо новий опорі план

Х4=
При такому опорному плані функція (3.17) стає рівною 1830 тис.т/міс, що менше попереднього значення 1980 тис.т/міс.
4-й крок. Аналізуємо новий опорний план (табл.3.5) на оптимальність. Знову знаходимо потенціали пунктів відправлення і пунктів призначення, для чого складаємо наступну систему рівнянь:
b1-a1=1, b1-a2=6, b1-a4=4,
b3-a1=3, b3-a3=4, b2-a4=1.
Вважаючи a1=0, знаходимо b1=1, b3=3, a2=-5, a3=-1, a4= -3, b2= -2. Для кожної вільної клітки обчислюємо числа αij: α12=-7, α22=-4, α23=-1, α31=0, α32=-8, α41=-5. Тому що серед чисел αij і немає строго позитивних, то опорний план Х3 є оптимальним.
Таблиця 3.5. Новий опорний план
| Пункт відправлення | Запас вантажу | Пункт призначення | Потенціал пункту відправлення ai | ||
| Потреба | |||||
| -5 | |||||
| -1 | |||||
| -3 | |||||
| Потенціал пункту призначення bi | -2 |
Різновиди транспортних задач
Розглянута математична модель (3.9) - (3.12) є класичною моделлю транспортної задачі. У реальній практиці економіста і менеджера, як правило, транспортна задача зустрічається в дещо іншій постановці. Математична модель реальної транспортної задачі може відрізнятися від класичної або видом цільової функції, або видом обмежень, або харак3ером змінних, або будь-яким сполученням перерахованих відмінностей одночасно.
Розглянемо декілька модифікацій транспортної задачі.
Транспортна задача про розподіл випуску продукції
При комплексному вирішенні проблеми виробництва і реалізації продукції виникає задача, що полягає у визначенні такого плану випуск і перевезень готової продукції, при якому досягаються мінімальні пні витрати на її виготовлення і доставку споживачам.
Для вирішення даної задачі розглядається повна собівартість виробництва одиниці продукції на кожному підприємстві (Si) і транспортні витрати (Sij), що залежать від типу застосовуваних транспортних засобів і районів розташування заводів-виробників і споживачів.
Математична модель такої задачі має вигляд:
m n
y=∑∑(si+sij)xij→min; (3.26)
i=1 j=1 xijÎΩ
m ____
Ω: fj=∑xij=bi, j=1,n; (3.27)
i=1
n ____
fn+i=∑xij=ai, i=1,m; (3.28)
j=1 _____ _______
xij≥0; i=1,m; i=1,m. (3.29)
_______ _______
xij=int; i=1,m; i=1,m. (3.30)
Якщо за умовою задачі потрібні ще капітальні вкладення в засоби транспорту, то показником ефективності служать приведені витрати, (3.26) матиме вигляд
 (3.31)
(3.31)
 - нормативний коефіцієнт ефективності капітальних вкладень; к - питомі капітальні вкладення, що приводяться на одиницю перевезень.
- нормативний коефіцієнт ефективності капітальних вкладень; к - питомі капітальні вкладення, що приводяться на одиницю перевезень.
Виконуючи підстановку  в цільову функцію (3.26) і підстановку
в цільову функцію (3.26) і підстановку  в цільову функцію (3.31), задача (3.26) - (3-30) і задача (3.31), (3.27) - (3.30) відповідно приводяться до класичної транспортної задачі, що може бути вирішена методом потенціалів.
в цільову функцію (3.31), задача (3.26) - (3-30) і задача (3.31), (3.27) - (3.30) відповідно приводяться до класичної транспортної задачі, що може бути вирішена методом потенціалів.
Розподільна транспортна задача про вибір засобів доставки вантажу
Змістовна постановка задачі. Нехай через j=1,2, ...,n позначено пункти, що мають вантажі для перевезень об'ємами aj відповідно. Є m засобів доставки вантажу (видів транспорту). Вантажопідйомність i-го засобу доставки складає рi а наявний його парк дорівнює bi, і=1,2,...,m... Вантажі підлягають доставці в один центральний пункт (склад). Витрати при здійсненні однією одиницею і-го засобу доставки від j-го пункту до складу дорівнюють Сij. Потрібно скласти найбільш економічний план доставки.
Математична модель задачі. Позначимо через Хij кількість засобів доставки і-го типу, що відправляється j-го пункту. Тоді математична модель розподільної транспортної задачі про вибір транспортних засобів має вигляд:
 (3.32)
(3.32)
 (3.33)
(3.33)
 (3.34)
(3.34)
 (3.35)
(3.35)
 (3.36)
(3.36)
Цільова функція (3.32) визначає сумарні витрати на доставку в вантажу на центральний склад. Вираз (3.33) вказує на необхідність вивезення всього вантажу з пунктів відправлення. Обмеження (3.34) вказує те, що кількість використовуваних засобів доставки не повинна перевищувати їхній наявний парк.
Поява параметра  ,- у системі обмежень (3.33) перешкоджає зведенню математичної моделі завдання до моделі класичної. Тому вирішувати її методом потенціалів неможливо. Вирішення даної задачі класичними методами лінійного програмування також неможливе через цілочисельність змінних
,- у системі обмежень (3.33) перешкоджає зведенню математичної моделі завдання до моделі класичної. Тому вирішувати її методом потенціалів неможливо. Вирішення даної задачі класичними методами лінійного програмування також неможливе через цілочисельність змінних  . Вирішення задачі можна одержати методом відсікання (шляхом введення в задачу додаткових обмежень у вигляді нерівностей Гомори), однак процедура вирішення різко ускладнюється. Тому вирішення задачі найбільш доцільно покласти на програм; Solver (Пошук рішення) інформаційної системи Microsoft Excel.
. Вирішення задачі можна одержати методом відсікання (шляхом введення в задачу додаткових обмежень у вигляді нерівностей Гомори), однак процедура вирішення різко ускладнюється. Тому вирішення задачі найбільш доцільно покласти на програм; Solver (Пошук рішення) інформаційної системи Microsoft Excel.
Транспортна задача про двохетапне перевезення вантажу
Змістовна постановка задачі. Однорідний вантаж потрібно доставити з т пунктів відправлення в п пунктів призначення. При доставці в пункти призначення вантажі можуть бути спочатку доставлені на р перевалочних пунктів. Задано вартості перевезень Су з кожного пункту відправлення в кожний пункт призначення і перевалочний пункт, а також вартості перевезення з кожного перевалочного пункту в пункт призначення.
Математична модель завдання. Позначимо:
 - вартість перевезення одиниці вантажу з i-го пункту відправлення j-й пункт призначення,
- вартість перевезення одиниці вантажу з i-го пункту відправлення j-й пункт призначення,  ;
;
 - вартість перевезення одиниці вантажу з i-го пункту відправлення в k-й перевалочний пункт
- вартість перевезення одиниці вантажу з i-го пункту відправлення в k-й перевалочний пункт  ;
;
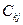 - вартість перевезення одиниці вантажу з к-го перевалочного пункту j-й пункт призначення
- вартість перевезення одиниці вантажу з к-го перевалочного пункту j-й пункт призначення 
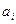 - запаси вантажу в i-м пункті відправлення;
- запаси вантажу в i-м пункті відправлення;
 - потреба у вантажі j-м пункті призначення;
- потреба у вантажі j-м пункті призначення;
 - місткість k-го перевалочного пункту;
- місткість k-го перевалочного пункту;
 - кількість вантажу, перевезеного з i-го пункту відправлення в j-й пункт призначення;
- кількість вантажу, перевезеного з i-го пункту відправлення в j-й пункт призначення;
 - кількість вантажу, перевезеного з і-го пункту відправлення в k-й перевалочний пункт;
- кількість вантажу, перевезеного з і-го пункту відправлення в k-й перевалочний пункт;
 - кількість вантажу, перевезеного з k-го перевалочного пункту в j-й пункт призначення.
- кількість вантажу, перевезеного з k-го перевалочного пункту в j-й пункт призначення.
Математична модель задачі з урахуванням вище наведених позначень може бути подана у вигляді задачі лінійного програмування:
 ; (3.37)
; (3.37)
 (3.38)
(3.38)
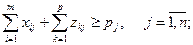 (3.39)
(3.39)
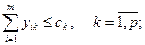 (3.40)
(3.40)
 (3.41)
(3.41)
 (3.42)
(3.42)
Тут цільова функція (3.37) складається з витрат трьох видів: на уставку частини вантажу з пунктів відправлення в пункти призначення, маючи перевалочні пункти; на перевезення частини вантажу з пункт призначення в перевалочні пункти; на доставку вантажу з перевалочних пунктів у пункти призначення. Система обмежень (3.38) говорить про те, що сумарні об'єми вантажів, що вивозяться з пунктів відправлення, не можуть перевищувати запаси вантажів у цих пунктах. Система обмежень (3.39) свідчить про те, що сумарні об'єми вантажів, що надходять у пункти призначення, не можуть бути менше відповідних потреб пунктів призначення. Система обмежень (3.40) означає, що сумарне завезення вантажів на кожний перевалочний пункт не може перевищувати його місткості. Система обмежень (3.41) вказує на те, що весь вантаж із перевалочних пунктів повинен бути вивезений повністю.
Як і в попередній задачі, математична модель (3.37) - (3.42) не може бути приведена до класичної. Тому вирішення задачі найбільш доцільно покласти на програму Solver (Пошук рішення) інформаційної системи Microsoft Excel.
Транспортна задача про двохетапне перевезення вантажу декількох видів
Змістовна постановка завдання. Вантаж, що включає q видів продукції, потрібно доставити з т пунктів відправлення в n пунктів призначення. При доставці в пункти призначення вантажі можуть бути спочатку доставлені на q перевалочних пунктів. Задано вартості перевезень для кожного виду вантажу з кожного пункту відправлення в кожний пункт призначення і перевалочний пункт, а також вартості перевезення з кожного перевалочного пункту в кожний пункт призначення.
Математична модель завдання. Позначимо:
 - вартість перевезення одиниці 1-го виду вантажу з г-го пункту відправлення в у-й пункт призначення,
- вартість перевезення одиниці 1-го виду вантажу з г-го пункту відправлення в у-й пункт призначення, 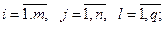
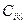 - вартість перевезення одиниці l-го виду вантажу з i-го пункту відправлення в к-й перевалочний пункт,
- вартість перевезення одиниці l-го виду вантажу з i-го пункту відправлення в к-й перевалочний пункт, 
 - вартість перевезення одиниці l-го виду вантажу з k-го перевалочного пункту в j-й пункт призначення,
- вартість перевезення одиниці l-го виду вантажу з k-го перевалочного пункту в j-й пункт призначення, 
 - запаси l-го виду вантажу в і-м пункті відправлення;
- запаси l-го виду вантажу в і-м пункті відправлення;
 - потреба в l-м виді вантажу j-м пункті призначення;
- потреба в l-м виді вантажу j-м пункті призначення;
 - місткість k-го перевалочного пункту стосовно l-го виду вантажу;
- місткість k-го перевалочного пункту стосовно l-го виду вантажу;
 - кількість l-го виду вантажу, перевезеного з i-го пункту відправлення j-й пункт призначення;
- кількість l-го виду вантажу, перевезеного з i-го пункту відправлення j-й пункт призначення;
 - кількість l-го виду вантажу, перевезеного з i-го пункту відправлення k -й перевалочний пункт;
- кількість l-го виду вантажу, перевезеного з i-го пункту відправлення k -й перевалочний пункт;
 - кількість l-го виду вантажу, перевезеного з k-то перевалочного пункту j-й пункт призначення.
- кількість l-го виду вантажу, перевезеного з k-то перевалочного пункту j-й пункт призначення.
Математична модель задачі з урахуванням вище приведених позначень може бути подана у вигляді задачі лінійного програмування:
 (3.43)
(3.43)
 (3.44)
(3.44)
 (3.45)
(3.45)
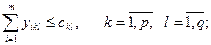 (3.46)
(3.46)
 (3.47)
(3.47)
 (3.48)
(3.48)
Математична модель задачі відрізняється від попередньої тільки там, що вона враховує різновид вантажів.
Транспортна задача про двохетапне перевезення вант декількох видів за запитами споживачів
Існує модифікація транспортної задачі двохетапного перевезення вантажів декількох видів, у якій кількість вантажу в пунктах відправлення не фіксована. Вона залежить від запитів споживачів.
Математична модель задачі. Позначимо:
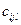 - вартість перевезення одиниці l-го виду вантажу з i-го пункту відправлення j-й пункт призначення,
- вартість перевезення одиниці l-го виду вантажу з i-го пункту відправлення j-й пункт призначення, 
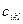 - вартість перевезення одиниці l-го виду вантажу з i-го пункту відправлення в k-й перевалочний пункт,
- вартість перевезення одиниці l-го виду вантажу з i-го пункту відправлення в k-й перевалочний пункт, 
 - вартість перевезення одиниці l-го виду вантажу з k-го перевалочного пункту в j-й пункт призначення,
- вартість перевезення одиниці l-го виду вантажу з k-го перевалочного пункту в j-й пункт призначення, 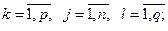
 - витрати на виробництво l-го виду вантажу в 2-м пункті відправлення;
- витрати на виробництво l-го виду вантажу в 2-м пункті відправлення;
 - потреба в l-м виді вантажу в j-м пункті призначення;
- потреба в l-м виді вантажу в j-м пункті призначення;
 - місткість k-то перевалочного пункту стосовно l-го вантажу;
- місткість k-то перевалочного пункту стосовно l-го вантажу;
 - кількість l-го виду вантажу, перевезеного з i-го пункту відправлення в j-й пункт призначення;
- кількість l-го виду вантажу, перевезеного з i-го пункту відправлення в j-й пункт призначення;
 - кількість l-го виду вантажу, перевезеного з i-го пункту відправлення в k-й перевалочний пункт;
- кількість l-го виду вантажу, перевезеного з i-го пункту відправлення в k-й перевалочний пункт;
 - кількість l-го виду вантажу, перевезеного з k-го перевалочного пункту в j-й пункт призначення;
- кількість l-го виду вантажу, перевезеного з k-го перевалочного пункту в j-й пункт призначення;
 - кількість виробленого l-го виду вантажу в i-м пункті відправлення.
- кількість виробленого l-го виду вантажу в i-м пункті відправлення.
Математичну модель задачі з урахуванням вище наведених значень можна подати у вигляді задачі лінійного програмування:
 (3.49)
(3.49)
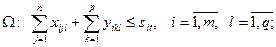 (3.50)
(3.50)
 (3.51)
(3.51)
 (3.52)
(3.52)
 (3.53)
(3.53)
 (3.54)
(3.54)
Цільова функція в математичній моделі (3.49) - (3.54) відрізняється від цільової функції (3.43) тільки тим, що враховує витрати на виробництво продукції (вантажу) в пунктах відправлення.
Транспортна задача про закриття підприємства
Змістовна постановка задачі Виробниче об'єднання складається з п заводів і т складів. Задано потреби складів у продукті й вартості на перевезення продуктів з кожного заводу на кожний склад. Задані фіксовані вартості функціонування заводів і можливості заводів по виробництву продукту. Виробниче об'єднання розглядає можливість закриття одного або декількох заводів. Це повинно зменшити витрати на перевезення. Які заводи, якщо це доцільно, повинні бути закриті?
Математичне формулювання завдання. Позначимо:
 - вартості перевезення j-го заводу на i-й склад;
- вартості перевезення j-го заводу на i-й склад;
 - потреби i-го складу в продукті, i=1,…,m;
- потреби i-го складу в продукті, i=1,…,m;
 - можливість j-го заводу по виробництву продукту;
- можливість j-го заводу по виробництву продукту;
 - фіксована вартість функціонування j-го заводу;
- фіксована вартість функціонування j-го заводу;
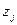 - булєве число, що показує, чи потрібно закрити j-й завод (значення 0), чи залишити його працювати (значення 1);
- булєве число, що показує, чи потрібно закрити j-й завод (значення 0), чи залишити його працювати (значення 1);
 - кількість перевезеного товару з j-го заводу на і-й склад.
- кількість перевезеного товару з j-го заводу на і-й склад.
Тоді математична модель транспортної задачі про закриття заводу може бути подана у такому вигляді:
 (3.55)
(3.55)
 (3.56)
(3.56)
 (3.57)
(3.57)
 (3.58)
(3.58)
 (3.59)
(3.59)
Тут цільова функція (3.55) визначає загальні витрати виробничої об'єднання на функціонування заводів і транспортування готової продукції на склади. Обмеження (3.56) визначає можливості заводів з виробництва продукції. Обмеження (3.57) визначають потреби складів у готовій продукції.
Читайте також:
- IV. Алгоритм вирішення задачі
- IV. Алгоритм розв’язання задачі
- IV. Алгоритм розв’язання задачі
- IV. Алгоритм розв’язання задачі
- IІI. Формулювання мети і завдань уроку. Мотивація учбової діяльності
- Rete-алгоритм
- V. ФОРМУЛЮВАННЯ ЗАВДАНЬ УРОКУ
- АЛГОРИТМ
- Алгоритм
- Алгоритм
- Алгоритм
- АЛГОРИТМ
| <== попередня сторінка | | | наступна сторінка ==> |
| Особливості задач лінійного програмування та практичні аспекти їх вирішення | | | Тема 4. Теорія достовірності та аналіз лінійних моделей оптимізаційних задач |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |