
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Оцінка зв’язку між факторами і критерії адекватності економетричної моделі
Для оцінки зв’язку між факторами економітеричної моделі використовують критерії: коефіцієнт кореляції і коефіцієнт детермінації.
Коефіцієнт кореляції показує ступінь впливу незалежних факторів (х) та залежну змінну (у). Цей критерій використовується в парних економетричних моделях – коефіцієнт парної кореляції, і в багатофакторних економетричних моделях – коефіцієнт множинної кореляції.
Коефіцієнт кореляції показує, на яку частину середнього квадратичного відхилення змінюється функція у, якщо аргумент х збільшується (зменшується) на своє середньоквадратичне відхилення σх. Знак коефіцієнта парної кореляції співпадає із знаком коефіцієнта регресії, а його чисельне значення коливається в межах
-1≤ry/х≤1. (9.4)
Коефіцієнт парної кореляції може бути визначений наступним чином []:
ry/х =  , (9.5)
, (9.5)
де ry/х – коефіцієнт парної кореляції;
 - середнє значення незалежної змінної Х;
- середнє значення незалежної змінної Х;
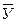 - середнє значення залежної змінної У;
- середнє значення залежної змінної У;
 - середнє квадратичне відхилення показника Х;
- середнє квадратичне відхилення показника Х;
 - середнє квадратичне відхилення показника У.
- середнє квадратичне відхилення показника У.
Слід відзначити, що середнє квадратичне відхилення визначається за формулою:
 , (9.6)
, (9.6)
де Dу - дисперсія (середній квадрат відхилення).
Відповідно, дисперсія визначається:
 , (9.7)
, (9.7)
де  - середній квадрат показника У;
- середній квадрат показника У;
 - квадрат середнього для показника У.
- квадрат середнього для показника У.
Аналогічні формули використовуються і для показника х.
Приклад. Розрахуйте коефіцієнти кореляції і детермінації на основі представлених в табл. 9.1 спостережень.
Таблиця 9.1. Таблиця вихідних даних для проведення розрахунків
| Спостереження | х | у |
| Сума | ||
| Середнє | 4,667 |
Вирішення
1. Визначимо дисперсію для факторів у і х. Для цього складемо табл. 9.2.
Таблиця 9.2 – Розрахунок середніх значень показників у і х
| Спостереження | х | у | х2 | у2 |
| Сума | ||||
| Середнє | 4,667 | 4,667 | 23,33 | |
| Квадрат середнього | 21,78 |
Використовуючи формулу 9.7 визначимо дисперсію для у і х:
 = 23,33 – 21,78 = 1,55
= 23,33 – 21,78 = 1,55
 = 4,667 – 4 = 0,667
= 4,667 – 4 = 0,667
2. Визначимо середнє квадратичне відхилення показників у і х, використовуючи формулу 9.6:
 =
=  = 1,24
= 1,24
 =
=  = 0,82
= 0,82
3. Використовуючи формулу 9.5 визначимо коефіцієнт парної кореляції для у і х:
ry/х = 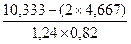 =
= 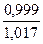 = 0,98.
= 0,98.
Значення коефіцієнту парної кореляції, що характеризують силу впливу показника х на у представлена в табл. 9.3.
Таблиця 9.3. Значення коефіцієнта парної кореляції
| Значення коефіцієнта кореляції | Сила впливу показника х на у |
| 0,85 - 1 | сильний |
| 0,55 – 0,84 | помірний |
| 0,25 – 0,54 | слабкий |
| 0 – 0,24 | дуже слабкий |
Знак значення коефіцієнта парної кореляції вказує на напрямок зв’язку. Якщо знак «+», то це вказує на прямо пропорційний зв’язок між факторами, якщо навпаки – то обернений.
Коефіцієнт множинної кореляції використовуються в багатофакторному економетричному аналізі. Його значення знаходиться в проміжку між 0 і 1. Сила впливу показників х на результуючий фактор у характеризується значеннями представленими в табл. 9.3.
Коефіцієнт детермінації визначається як квадрат коефіцієнту кореляції:
Dy/x = r2y/x або (9.8)
Dy/xі= R2y/xi (9.9)
Основними напрямками оцінки адекватності економетричної моделі є:
1. Перевірка за допомогою F-тесту (F-критерій Фішера);
2. Використання t-розподілу Ст`юдента для оцінки надійності коефіцієнта кореляції;
3. Перевірка моделі на гомо-гетескедастичність;
4. Перевірка факторів економетричної моделі на мультиколінеарність.
F-тест використовується для оцінки того, чи важливе пояснення, яке дає рівняння в цілому. Цей тест заснований на порівнянні залишкової теоретичної дисперсії  2y/х і загальної дисперсії σy2. Розглядається відношення
2y/х і загальної дисперсії σy2. Розглядається відношення  і порівнюється з табличним (для
і порівнюється з табличним (для 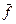 % Фішера знайдено розподіл і складена спеціальна таблиця) при заданому рівні значущості і різних ступенях свободи.
% Фішера знайдено розподіл і складена спеціальна таблиця) при заданому рівні значущості і різних ступенях свободи.
Загальна дисперсія σy2 досліджених даних від їх середнього значення встановлюється з урахуванням числа ступенів свободи 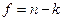 :
:
 , (9.8)
, (9.8)
де К – число інтервалів у вибіркових даних.
Залишкова теоретична дисперсія  2y/х встановлюється як різниця розрахункових
2y/х встановлюється як різниця розрахункових 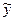 i і середніх інтервальних значень
i і середніх інтервальних значень  i з урахуванням числа ступенів свободи d1=K-P і d2=n-K,
i з урахуванням числа ступенів свободи d1=K-P і d2=n-K,
де Р – число параметрів управління.
Якщо 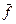 рас ≤
рас ≤ 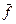 табл, то при заданому рівні значущості складене рівняння регресії затверджується. Вірогідність помилки тим менше чим більше рівень значущості α%.
табл, то при заданому рівні значущості складене рівняння регресії затверджується. Вірогідність помилки тим менше чим більше рівень значущості α%.
У разі, коли чисельник  2y/х менше знаменника σy2, то міняємо їх місцями разом з відповідними ступенями свободи d1=K-P і d2=n-K.
2y/х менше знаменника σy2, то міняємо їх місцями разом з відповідними ступенями свободи d1=K-P і d2=n-K.
Приклад. Загальна дисперсія σy2=41,5 при n=154 і К=12.
Залишкова дисперсія  2y/х=34,44 при К=12 і Р=3 (Р=3 в квадратному рівнянні регресії).
2y/х=34,44 при К=12 і Р=3 (Р=3 в квадратному рівнянні регресії).
Вирішення
 , оскільки σy2>
, оскільки σy2>  2y/х, переходимо до відношення із ступенями свободи D1=154-12=142, d2=12-3=9
2y/х, переходимо до відношення із ступенями свободи D1=154-12=142, d2=12-3=9 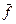 розр.=
розр.=  =1,21,
=1,21,
за таблицею 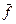 5%(142,9)=2,75
5%(142,9)=2,75 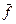 20%(142,9)=1,7.
20%(142,9)=1,7.
Отже, знайдене квадратне рівняння регресії з високою надійністю узгоджується з вихідними даними.
Слід відзначити, що в регресійному аналізі побудова F-статистики здійснюється шляхом відношення дисперсії залежної змінної на “пояснювальні” і “непояснювальні” складові:
F = (ESS / k) / RSS / (n-k-1), (9.11)
де ESS - пояснювальна сума квадратів відхилень;
RSS – залишкова (непояснювальна) сума квадратів;
к – кількість ступенів свободи;
n – кількість значень факторів моделі.
При здійсненні F-теста для рівняння перевіряється, чи перевищує r2 те значення, яке може бути отримано випадково. Для розрахунку F-статистики для рівняння в цілому, формулу (9.9) можна трасформувати шляхом ділення чисельника і знаменника рівняння на TSS (загальну суму квадратів), відмічаючи, що ESS/TSS дорівнює r2, а RSS/TSS дорівнює (1 - r2). В результаті отримуємо наступне рівняння:
F= r2 / к / (1 - r2) / (n – k - 1). (9.12)
Розрахунковий F-критерій визначається при відповідному рівні значущості і ступенях свободи і порівнюють з критичним F-критерієм Фішера. Значення останнього критерію представлені в спеціальних таблицях. Якщо розрахунковий F-критерій перевищує його критичне значення, то можна стверджувати, що пояснення, яке дає рівняння в цілому важливе, а економетрична модель адекватна. У протилежному випадку – модель вважається неадекватною, а пояснення неважливе.
Іншим важливим статистичним параметром для перевірки адекватності економетричної моделі є t-розподіл Ст’юдента. Він використовується для оцінки надійності коефіцієнта кореляції. В цьому випадку t-статистика для r розраховується наступним чином:
 |
t = √n-2/1-r2. (9.13)
Вибравши рівень значущості в 5% дослідним знаходить критичне значення t з (n - 2) ступенями свободи. Якщо значення t перевищує його критичне значення (позитивний або негативний бік), то нульову гіпотезу відхиляють про те, що коефіцієнт кореляції дорівнює нулю. В цьому випадку роблять висновок про лінійний зв’язок (позитивний або негативний).
Слід відзначити, якщо нульова гіпотеза підтверджується, то значення t буде перевищувати його критичне значення (в позитивний або негативний бік) тільки в 5% випадках. Це означає, що при виконанні перевірки ймовірності допущення помилки, що відхиляє нульову гіпотезу, коли вона фактично вірна, складає 5%.
Ймовірно, що ризик допущення такої помилки в 5% випадків досить великий для дослідника. Тоді він може скоротити ступінь ризику, здійснюючи розрахунки при рівні значущості в 1%. Критичне значення t зараз буде вище, ніж до цих пір, тому необхідна більш висока (позитивна або негативна) t-статистика для відхилення нульової гіпотези, а це означає, що потрібно більш вище значення коефіцієнта кореляції.
Слід вказати і на те, що t-статистика може бути розрахована як співвідношення оцінки коефіцієнта регресії на стандартну помилку.
Розглянемо методику розрахунку F-критерію і t-статистики на прикладі.
Приклад. Виконайте відповідні t-тести для багатофакторної моделі. Розрахуйте F-критерій, якщо відомо, що кількість спостережень дорівнює 25, коефіцієнт детермінації (R2) дорівнює 88%. Багатофакторна економетрична модель має вигляд:
у = 55,3 + 0,093х1 + 0,087х2. (9.14)
Стандартні помилки дорівнюють: постійний член – 2,4, х1 – 0,003, х2 – 0,002.
Вирішення
Для t-тест необхідно визначити розрахунковий t-критерій. Для кожного із члена економетричного рівняння він розраховується окремо як співвідношення оцінки коефіцієнта регресії на стандартну помилку. Таким чином розрахункові t-критерій наступні:
tр1 = 55,3/2,4 = 23,04;
tр2 = 0,092/0,003 = 30,67;
tр3 = 0,067/0,002 = 43,5.
Наступним кроком проведення t-теста є порівняння розрахункових значень із табличними. Табличне значення t-критерію визначається на основі спеціальних таблиць при відповідних рівнях значущості (5% або 1%) і ступенях свободи, які визначаються (n – k – 1, де n – кількість спостережень; k – кількість факторів моделі, включаючи постійний параметр).
В нашому випадку ступеня свободи дорівнюють – 25 – 4 – 1 = 20.
Табличне значення t-критерію при рівні значущості в 5% дорівнює 1,725; при 1% - 2,528.
Як видно розрахункові значення t-критеріїв всіх факторів моделі значно перевищують його табличні значення. Це означає, що всіх фактори економетричної моделі суттєво впливають на змінний показник (у).
F-критерій визначається за формулою 9.10. Для розробленої економетричної моделі розрахункових F-критеріїв має наступне значення: Fр = (0,88/4) / ((1 – 0,88) / (20)) = 36,7.
Потім розрахункове значення F-критерію порівнюємо із його табличним значенням при відповідному рівні значущості і кількості спостережень.
При 5% рівні значущості для 25 спостережень табличний F-критерій дорівнює 2,99, при 1% - 29,46.
Таким чином, розрахункові значення F-критерію більше табличних, що вказує на суттєвий рівень пояснення причинно-наслідкових зв’язків економітричної моделі.
Наступним етапом оцінки адекватності економетричної моделі є перевірка її на гетеро- або гомоскедастичність. Гомоскедастичність означає однаковий розподіл фактичних значень вибірки змінних. Тобто фактичні значення спостережень іноді будуть позитивними, іноді негативними, іноді – відносно близькими до нуля, проте в апріорі відсутні причини появи великих відхилень між спостереженнями.
Разом з тим, для деяких вибірок, можливо, більш доцільно припустити, що теоретичний розподіл випадкового члену є різним для різних спостережень. Це не означає, що випадковий член обов’язково буде мати особливо більші (позитивні або негативні) значення в кінці вибірки, проте це означає, що апріорна ймовірність отримання більш відхилених значень буде відносно висока. Це є прикладом гетероскедастичності, що означає “неоднаковий розподіл”.
Гетероскедастичність стає проблемою, коли значення змінних, які включаються в рівняння регресії, значно відрізняються в різних спостереженнях. Якщо залежність може буде описана рівнянням, в якому економічні показники змінюють свій масштаб одночасно, то зміна значень невключених змінних і помилок виміру, впливаючи разом на випадковий член, роблять його порівняно незначними при незначних у і х і порівняно великими – при великих у і х.
Досить часто можна виявити проблему гетероскедастичності. В таких умовах можна здійснити відповідні дії по виключенню цього ефекту на етапі специфікації моделі регресії, і це дозволить зменшити або, можливо, усунути необхідність формальної перевірки. В теперішній час запропоновано значна кількість тестів (і, відповідно, критеріїв для них). Найбільш поширеними тестами є: тест рангової кореляції Спірмена, тест Голфреда-Квандта і тест Глейзера.
При виконання теста рангової кореляції Спірмена припускається, що дисперсія випадкового члену буде або збільшуватися, або зменшуватися відповідно збільшення змінної х, і тому в регресії, абсолютні значення залишків і значення х будуть корельовані. Дані по х і залишки упорядковуються, і коефіцієнт рангової кореляції визначається як:
rx,e = 1 – (6ΣD2i/n(n2 - 1)), (9.15)
де Di – різниця між рангом х і рангом помилки е;
е – залишки.
Якщо припускати, що відповідний коефіцієнт кореляції для генеральної сукупності дорівнює нулю, то коефіцієнт рангової кореляції має нормальний розподіл з математичним очікуванням 0 і дисперсією 1/(n - 1) в більших вибірках. Таким чином, відповідна тестова статистика дорівнює rx,e  , і при використанні двобокового критерію нульова гіпотеза про відсутність гетероскедастичності буде відхилена при рівні значущості в 5%, якщо вона перевищує 1,96, і при рівні значущості в 1%, якщо вона перевищує 2,58. Якщо в моделі регресії знаходиться більш однієї пояснювальної змінної, то перевірка гіпотези може здійснюватися з використанням іншої з них.
, і при використанні двобокового критерію нульова гіпотеза про відсутність гетероскедастичності буде відхилена при рівні значущості в 5%, якщо вона перевищує 1,96, і при рівні значущості в 1%, якщо вона перевищує 2,58. Якщо в моделі регресії знаходиться більш однієї пояснювальної змінної, то перевірка гіпотези може здійснюватися з використанням іншої з них.
Ймовірно, найбільш відомим формальним критерієм є критерій, запропонований С. Голдфелдом і Р. Квандтом. При проведенні перевірки по цьому критерію припускають, що стандартне відхилення (σі) розподілу ймовірностей Uі пропорційно значенню х в цьому спостереженні. Запропоновано також, що випадковий член розподілений нормально і не піддається автокореляції.
Всі n спостережень у виборці упорядковуються по значенню х, після чого оцінюється окремі регресії для перших n’ і для останніх n’ спостережень; середні (n - 2n’) спостережень відхиляються. Якщо припущення відносно природи гетероскедастичності доцільно, то дисперсія U і в останніх n’ спостереженнях буде більшою, чим в перших n’, і це буде відображено в сумі квадратів залишків в двох вказаних “часткових” регресіях. Визначаючи суми квадратів залишків в регресіях для перших n’ і останніх n’ спостережень відповідно через RSS1 i RSS2. Розрахуємо відношення RSS2/RSS1, яке має F-розподіл з (n’ – к - 1) і (n’ – к - 1) ступенями свободи, де к – число пояснювальних змінних в регресійному рівнянні. Потужність критерія залежить от вибору n’ по відношенню до n. Ґрунтуючись на результатах деяких проведених експериментів, С. Голдфелд і Р. Кванд стверджують, що n’ повинно складати порядок 11, коли n = 30, і порядку 22, коли n = 60. Якщо в моделі знаходиться більш однієї пояснювальної змінної, то спостереження повинні упорядковуватися по тій з них, яка, як запропоновано, пов’язана з σі і n’ повинно бути більше, ніж к + 1 (де к – число пояснювальних змінних).
Метод Голдфелда-Квандта може бути також використаний для перевірки на гетероскедастичність при припущенні, що σі обернено пропорційний хі. При цьому використовується подібна процедура, що і розглянута вище, проте тестова статистика зараз є показником RSS1/RSS2, який знову має F-розподіл з (n’ – к - 1) і (n’ – к - 1) ступенями свободи.
Тест Глейзера дозволяє більш ретельно розглянути характер гетероскедастичності. Він ґрунтується на тому, що знімається припущення, що σі пропорційна хі, а перевіряється лише більш подібна функціональна форма.
Для того, щоб використовувати цей метод, необхідно оцінити регресійну залежність у від х за допомогою методу найменших квадратів, а потім розрахувати абсолютні значення залишків е, оцінивши їх регресію. В кожному випадку нульова гіпотеза про відсутність гетероскедастичності буде відхилена, якщо оцінка регресії відрізняється від нуля. Якщо при оцінюванні більше однієї функції, то орієнтиром при визначенні характеру гетероскедастичності може служити найкраща з них.
В цьому розділі представлені основні критерії й тести щодо оцінки адекватності моделі. В економетричних дослідженнях можна використовувати й інші тести і критерії. Представлені критерії оцінки адекватності економетричної моделі дають змогу отримати більш ґрунтовні і, насамперед, об’єктивні результати тих економічних процесів, які відбуваються на підприємстві.
Читайте також:
- A) Оцінка захисних споруд за ємністю – визначення коефіцієнта Квм.
- B) Оцінка ЗС за захисними властивостями
- CMM. Визначення моделі зрілості.
- II.3. Основні способи і прийоми досягнення адекватності
- III. GPSS — програма імітаційної моделі ЕОМ
- III. КРИТЕРІЇ ДОПУСКУ ДО СКЛАДАННЯ ПІДСУМКОВОГО МОДУЛЬНОГО КОНТРОЛЮ (ЕКЗАМЕНУ).
- ISO 15504.Структура еталонної моделі
- IV. Загальна оцінка діяльності вчителя
- IV. Оцінка вигідності залучення короткотермінових кредитів
- IV. Оцінка привабливості стратегічних зон господарювання підприємства на ринку.
- V. ЗАХИСТ КУРСОВОЇ РОБОТИ ТА КРИТЕРІЇ ОЦІНЮВАННЯ
- V. КРИТЕРІЇ ОЦІНЮВАННЯ КУРСОВОЇ РОБОТИ
| <== попередня сторінка | | | наступна сторінка ==> |
| Принципи побудови економетричних моделей | | | Сутність мультиколінеарності, напрями її виявлення |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |