• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Керування багатопродуктовими запасами

Основні характеристики моделі керування багатопродуктовими запасами:

1) система постачання забезпечує попит на продуктів протягом

одного року.

2) Для поповнювання запасів система має необхідні виробничі поту­жності. Витрати на підготовчо — заключні операції, які вважають витратами

на поставку, пропорційні до числа поставок поставки:

(4.1)

де — річна потреба в -му продукті; — витрати на підготовчо заключні операції на виготовлення однієї партії поставки -го продукту (не залежить від розміру партії поставки ).

3) Поставки миттєві.

4) Дефіцит виключається ( = 0 ).

5) Витрати на зберігання, зумовлені зв'язуванням оборотних фондів у запасах протягом року, пропорційні до середньої вартості запасу і часу його існування:

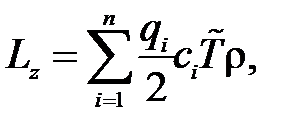(4.2)

де — ціна за одиницю — го продукту; — кількість одиниць часу в одному році;

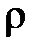— коефіцієнт нарахування на зв'язані оборотні фонди, фізична розмірність якого =

Якщо за одиницю часу вибрати рік(тобто в усіх величинах моделі фізичну розмірність часу подати відносно цієї одиниці), то формула (4.2) дещо спроститься:

(4.3)

6) Заданий норматив Е оборотних фондів щодо величини запасу (середня вартість запасу має не перевищувати цієї величини), тобто:

(4.4)

або

(4.5)

7) Знайти значення , які мінімізують річні витрати на організацію

постачання

(4.6)

Принципи побудови економіко-математичної моделі.Підставивши в (5.18) значення складових витрат згідно з виразами (4.1) і (4.3), дістанемо цільову функцію оптимізаційної задачі:

(4.7)

Обмеженнями задачі буде формалізована вимога щодо додержання нормативу на оборотні фонди (5.17), а також умова невід’ємності

(4.8)

Економіко-математична модель – цільова функція (4.7) разом з обмеженнями (4.5) і (4.8) – належить до задач цілочислового лінійного програмування. Для її розв’язання найдоцільніше застосовувати метод множників Лагранжа.

Читайте також:

1. D-тригер з динамічним керуванням
2. IV Етап: Вибір стратегії керування виявленими ризиками й виділення пріоритетних напрямків роботи
3. Автократично-демократичний континуум стилів керування.
4. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
5. Автоматизація меліоративних помпових стацій. Автоматизація керування помповими агрегатами.
6. Агресивне керування портфелем акцій
7. Алгоритми керування ресурсами
8. Аналіз конструкції рульового керування.
9. Аналіз умов технічної експлуатації територіально розподілених ПФС екстремальної комп’ютерно-інтегрованої системи керування технологічними процесами обробки даних
10. Апарати керування пневматичними приводами.
11. АУДИТ ОПЕРАЦІЙ З ЗАПАСАМИ
12. Багатокритеріальні завдання оптимального керування

Переглядів: 419