• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Концептуальна імітаційна модель керування запасами

Імітаційна модель керування запасами має такі основні передумови:

1. Моделюється однопродуктова система керування запасами. Кількість продукту, яка вивозиться щоденно зі складу, визначається поточним попитом. Використовується стратегія фіксованого розміру замовлення (h, q): коли рівень поточного запасу y падає нижче від заданої позначки h, керівництво складу замовляє поставку товару в кількості q. Після закінчення терміну виконання замовлення ця продукція надходить на склад і доповнює запас, що вже є там у даний момент. Система постачання функціонує 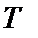днів.

2. Щодня виникає попит на предмет зберігання, причому дорівнює цей попит величині 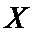— випадковій величині з відомим законом розподілу ймовірностей.

3. Встановлюється такий порядок виконання операцій на складі протягом кожного дня:

1) визначаються обсяги замовлень на поповнення запасу, які будуть реалізовані протягом поточного дня;

2) товар поставляється споживачеві, тобто задовольняється попит;

3) оцінюється запас, що залишився, і в разі потреби (якщо поточний запас досягає порогового рівня) оформляється замовлення на поповнення запасу.

4. Затримка поставки 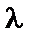(кількість днів між моментами часу подачі замовлення на поставку та її надходженням) тлумачиться як випадкова величина з відомим законом розподілу ймовірностей.

5. Незадоволені замовлення споживачів товару анулюються, тобто переносити дефіцит на наступний день не дозволяється.

6. Заявка на поповнення запасу приймається до виконання лише в тому разі, коли подана раніше заявка реалізована, тобто в кожний момент часу на стадії реалізації не може перебувати більш як одна заявка.

7. За цільову функцію для вибору оптимальних значень змінних керування беруть сумарні витрати (вартість зберігання і поставки, штраф) за період .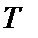

.

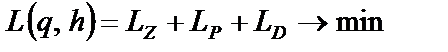Оскільки щоденний попит і затримка поставок — випадкові величини, то й сума витрат системи постачання 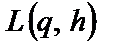також є випадковою величиною, закон розподілу ймовірностей якої в загальному випадку невідомий. Тому цільова функція являє собою математичне сподівання витрат M [ ].

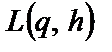8. Математичне сподівання витрат при фіксованих значеннях змін­них керування 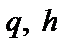оцінюється з допомогою вибіркового середнього

,

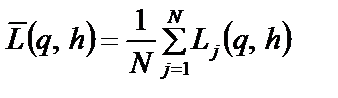де N — число циклів прогонів (дублювань) імітаційної моделі при фіксованих значеннях змінних керування 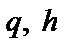і незмінних факторах моделі (у разі машинної реалізації імітаційної моделі беруть 1000 циклів прогонів); 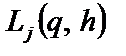— значення сумарних витрат у j-му прогоні.

9. Вартість поставки — стала величина, що не залежить від обсягу поставки і дорівнює :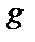

.

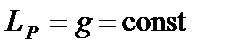10. Вартість зберігання пропорційна до величини залишку продукту на кінець дня, коефіцієнт пропорційності дорівнює .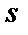

11. Витрати на штрафи пропорційні до залишкової величини дефіциту на кінець дня, коефіцієнт пропорційності дорівнює .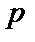

12. Ендогенна змінна системи (відгук): 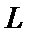— сумарні витрати.

13. Змінні, що визначають стан системи в довільний момент часу:

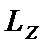— витрати на зберігання;

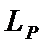— вартість поставки;

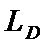— витрати на штрафи;

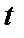— поточний (системний, модельний) час;

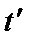— момент часу (день), коли реалізується поставка;

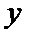— поточне значення запасу (у разі дефіциту — від’ємне);

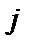— індекс циклів роботи імітаційної моделі.

14. Змінні керування:

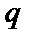— обсяг (партія) замовленої поставки;

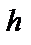— нижній (пороговий) рівень запасу.

15. Некеровані параметри:

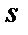— витрати на зберігання одиниці продукції на кінець дня;

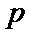— витрати через дефіцит, пов’язані з нестачею одиниці продукції;

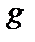— витрати на організацію однієї поставки;

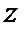— початковий рівень запасу;

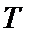— тривалість (кількість днів) функціонування системи постачання.

16. Екзогенні (вхідні) змінні:

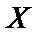— щоденний попит на продукт;

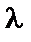— час затримки поставки.

17. Характеристики функціонування системи:

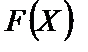— функція розподілу ймовірності попиту;

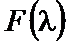— функція розподілу ймовірності затримки поставки.

18. За допомогою методу імітаційного моделювання потрібно знайти оптимальні значення 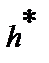і 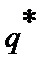, при яких сумарні витрати на організацію постачання протягом 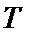днів будуть мінімальні. Для експериментального пошуку оптимального розв’язку задачі застосовується метод Бокса–Уїлсона.

Читайте також:

1. CMM. Модель технологічної зрілості. Зрілі і незрілі організації.
2. D-тригер з динамічним керуванням
3. Demo 7: Модель OSI (модель взаімодії відкритих систем)
4. G2G-модель електронного уряду
5. IV Етап: Вибір стратегії керування виявленими ризиками й виділення пріоритетних напрямків роботи
6. O модель привабливість - конкурентоспроможність (матриця Мак Кінсі).
7. OSI - Базова Еталонна модель взаємодії відкритих систем
8. V – модель
9. Абстрактна модель
10. Абстрактна модель
11. Абстрактна модель оптимального планування виробництва
12. Автократично-демократичний континуум стилів керування.

Переглядів: 659