• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Перевірку значущості оцінок

Перевірку значущості оцінок коефіцієнтів проводять за допомогою t —критерія Стюдента:

із ступенями свободи (m — число паралельних дослідів).

Рівняння регресії після перетворення змінних запишеться у формі

,

де .

Дисперсію коефіцієнта оцінюють по формулі

.

2.7 Перевірка адекватності математичного опису. Щоб перевірити гіпотезу про адекватність математичного опису експериментальним даним, достатньо оцінити відхилення передбаченої по одержаному рівнянню регресії величини відгуку від результатів спостережень в одних і тих же g—x точках факторного простору. Розсіяння результатів спостережень поблизу рівняння регресії, що оцінює істинну функцію відгуку, можна охарактеризувати за допомогою дисперсії адекватності

де d — число членів апроксимуючого полінома. Дисперсія адекватності визначається за числом ступенів свободи

.

Перевірка гіпотези про адекватність полягає, по суті справи, в з'ясуванні співвідношення між дисперсією адекватності і оцінкою дисперсії відтворності відгуку . Якщо ці оцінки дисперсій однорідні, то математичний опис адекватно представляє результати експерименту, якщо ж ні, то опис вважається неадекватним. Перевірку гіпотези про адекватність проводять з використанням F- критерия Фішера. Критерій Фішера дозволяє перевірити гіпотезу про однорідність двох вибіркових дисперсій і . В тому випадку, якщо > , F-критерій характеризується відношенням

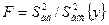
Якщо обчислене за наслідками наглядів емпіричне значення критерію F менше критичного 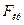, знайденого з Додатків VI —IX для відповідних ступенів свободи

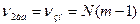
при заданому рівні значущості 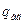, то гіпотезу про адекватність не відкидають. Інакше гіпотезу відкидають і математичний опис признається неадекватним.

Перевірка адекватності можлива при . Якщо число N варіантів варіювання плану ПФЕ рівне числу всіх значущих оцінок коефіцієнтів регресії (N=d), то для перевірки гіпотези про адекватність математичного опису ступенів свободи не залишається ( ). Якщо ж деякі оцінки коефіцієнтів регресії виявилися незначущими, то число d членів рівняння в цьому випадку, що перевіряється, менше числа N варіантів варіювання (N>d) і для перевірки гіпотези про адекватність залишиться одна або декілька ступенів свободи .

У тому випадку, коли гіпотеза про адекватність відкидається, необхідно переходити до складнішої форми математичного опису або, якщо це можливо, проводити експеримент з меншим інтервалом варіювання . Слід зазначити, що максимальна величина інтервалу варіювання визначається умовою адекватного опису об'єкту в області варіювання. Якщо при великих інтервалах варіювання математична модель неадекватна, то виникають систематичні помилки у визначенні коефіцієнтів, для зменшення яких слід звузити область варіювання. Проте із зменшенням інтервалу варіювання з'являється цілий ряд нових труднощів: росте відношення перешкоди до корисного сигналу, що приводить до необхідності збільшувати число паралельних дослідів для виділення корисного сигналу на фоні шуму, тобто зменшуються абсолютні значення оцінок коефіцієнтів, величини яких безпосередньо залежать від .

Оскільки визначувані за наслідками експерименту коефіцієнти, рівняння (17) служать лише оцінками істинних значень коефіцієнтів рівняння регресії, то одержане рівняння є лише вибірковим з деякої генеральної сукупності. Таким чином, результат прогнозу вихідної величини за допомогою рівняння (17) залежить від оцінок коефіцієнтів. Правомірно порівняти прогноз , одержаний за допомогою вибіркового рівняння (17), із істинним значення . В цьому випадку мова може йти про точність прогнозу значення вихідної величини в заданій точці чинника простору по одержаному поліному, яка оцінюється дисперсією

.

Критерій ортогональності є недостатньо сильним критерієм оптимальності для планування другого порядку. При ортогональному плануванні другого порядку дисперсії оцінок коефіцієнтів міняються при повороті координат, тобто точність прогнозу вихідної величини в різних напрямах факторного простору неоднакова.

Читайте також:

1. Git виконує перевірку цілісності даних
2. Асимптотичний підхід до порівняння оцінок
3. Бальна система оцінок технічного стану газопроводів
4. Вибір алгоритмів розрахунку комплексних порівняльних оцінок.
5. ВИДИ ЕКСПЕРТНИХ ОЦІНОК
6. Види педагогічного оцінювання і педагогічних оцінок.
7. Відповідність підсумкових модульних рейтингових оцінок у балах оцінкам за шкалою ECTS та національною шкалою
8. Відповідність рейтингових оцінок за окремі види навчальної роботи у балах оцінкам за нац. шкалою
9. Для отримання кінцевого результату (експертних оцінок) використовують анкетні методи і методи групової експертизи.
10. Допуск до роботи осіб, які не пройшли навчання, інструктажі і перевірку знань з охорони праці, забороняється.
11. Експертних оцінок.
12. Європейська шкала оцінок

Переглядів: 368