• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Інтервальні оцінки для генеральних середньої та частки

Інтервальною оцінкою (абонадійним,абодовірчим інтервалом)параметра генеральної сукупності називається такий інтервал , який із заданою надійністю (абонадійною,абодовірчою імовірністю) γ накриває параметр , що оцінюється. При цьому , , де – точкова оцінка (або вибіркове значення) параметра , величина δ знаходиться за нижченаведеними формулами і визначає точність інтервальної оцінки: чим менше δ, тим вища точність.

У статистиці величина δ називається граничною помилкою і обчислюється за формулою:

δ=t* μ,

де величина t називається довірчим числом (або коефіцієнтом довіри), а μ – середньою (абостандартною) помилкою.

Довірче число t=t_γ (n) знаходиться за таблицями критичних точок розподілу Стьюдента для двосторонньої критичної області в залежності від надійності γ і обсягу вибірки п (див. додаток 3, число степенів вільності k=n–1, рівень значущості α=1–γ). Так, наприклад, t_0,95(10)=2,26.

Якщо п>30, то прийнято вважати, що розподіл Стьюдента з достатньою для практичних потреб точністю співпадає з нормальним розподілом і тоді число t=t_γ можна знаходити за таблицями значень інтегральної функції Лапласа Ф(х) (див. додаток 5) із умови: Ф(t_γ )=γ/2. Так, наприклад, t_0,95=1,96. Крім того, число t_γ можна знаходити за таблицею додатку 3, поклавши .

Середні помилки μ для інтервальних оцінок генеральної середньої та генеральної частки р знаходяться за формулами, наведеними в таблиці 2.1:

Таблиця 2.1

Середні помилки інтервальних оцінок параметрів тар

Схема відбору	для (п>30)	для ( )	для р
Повторна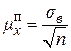
Безповторна

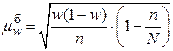
Позначення: – вибіркове середнє квадратичне відхилення, яке обчислюється за формулою (1.7), наведеною в л. р. № 1 для відповідного варіаційного ряду: з. в. р., д. в. р. чи і. в. р.; – виправлене середнє квадратичне відхилення; 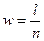– вибіркова частка варіант, що задовольняють задану умову; l – число варіант, що задовольняють задану умову; N – обсяг генеральної сукупності.

Точковимиоцінками генеральних середньої та частки р є відповідно вибіркові середня та частка w; при цьому обчислюється за формулами (1.1) – (1.3), наведеними в л. р. № 1 для відповідного варіаційного ряду: з. в. р., д. в. р. чи і. в. р.

Таким чином, надійні інтервали для генеральних середньої та частки мають такий вид:

– для повторної вибірки:

, якщо п>30; (2.1)

, якщо п≤30; (2.2)

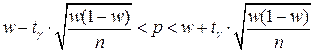. (2.3)

– для безповторної вибірки:

, якщо п>30; (2.4)

, якщо п≤30; (2.5)

. (2.6)

Очевидно, якщо обсяг вибірки п набагато менший за обсяг генеральної сукупності N (n<<N), то n/N ≈ 0 і формули (2.1) – (2.3) майже збігаються з формулами (2.4) – (2.6). Тому у статистичній практиці прийнято вважати, що якщо n/N < 0,05, то надійні інтервали можна знаходити за більш простими формулами (2.1) – (2.3) незалежно від схеми відбору.

Слід зауважити, що формули для μ_х та μ_w виведено в припущенні відповідно нормального та біноміального розподілів генеральної сукупності, проте на практиці вони використовуються незалежно від виду розподілу останньої.

Читайте також:

1. II. ПОРЯДОК ПРОВЕДЕННЯ ТА ОЦІНКИ ПОТОЧНИХ ТА ПІДСУМКОВИХ ЗАНЯТЬ (ЗМІСТОВИХ МОДУЛІВ).
2. II. ПОРЯДОК ПРОВЕДЕННЯ ТА ОЦІНКИ ПОТОЧНИХ ТА ПІДСУМКОВИХ ЗАНЯТЬ (ЗМІСТОВИХ МОДУЛІВ).
3. O стратегія підвищення ринкової частки за існуючої місткості ринку.
4. X. Зарахування вступників на основі повної загальної середньої освіти, які досягли визначних успіхів у вивченні профільних предметів
5. А) Мета і об'єкти грошової оцінки
6. Адекватним фізичним критерієм оцінки її впливу на організм люди1
7. Алгоритм безпосередньої заміни
8. Алгоритм виявлення, оцінки та зменшення ризиків виникнення небезпечних ситуацій на виробництві ( СРС – «А»)
9. Аналіз відхилень – основний інструмент оцінки діяльності центрів відповідальності
10. Аналіз відхилень — основний інструмент оцінки діяльності центрів відповідальності
11. Аналіз динаміки частки ринку на основі прихильності до марки
12. Аналіз загальної рівноваги розширює можливості оцінки ефективності функціонування ринкової економіки.

Переглядів: 457