• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Метод кореляції рангів Спірмена

Перш за все підкреслимо, що для даного методу справедливим є зауваження із п.2.5.

Даний метод належить до так званих непараметричних методів наближеного оцінювання зв’язку, оскільки його застосування не потребує обчислення будь-яких параметрів сукупності, що вивчається.

Метод кореляції рангів Спірмена:

а) застосовується у випадках, коли обидві ознаки (або одна з них) є атрибутивними або варіаційними, але шкала атрибутивної ознаки може розглядатись як рангова;

б) дає можливість формально (але наближено) перевіряти істотність і оцінювати щільність зв’язку, а також визначати його напрям;

в) не дає можливості визначати вид та характер залежності.

Числовою мірою істотності та щільності зв’язку в даному методі є коефіцієнт кореляції рангів Спірмена

, (3.21)

де d_i=u_i–v_i – різниця рангів u_i та v_i для відповідно х_і та у_і, п – число пар (х_і; у_і). Можна показати, що [‑1; 1].

Рангомu_i(v_i) кожного значення х_і(у_і) є його порядковий номер, якщо всі х_і(у_і) розташувати у неспадному порядку. Якщо при цьому деякі значення х_і(у_і) збігаються, то кожному з них присвоюється ранг, що дорівнює середньому арифметичному їх фактичних порядкових номерів.

Для перевірки істотності (тобто існування) зв’язку необхідно за формулою (3.21) обчислити спостережене значення величини і порівняти його модуль з критичним значенням , яке залежить від обсягу сукупності п та рівня значущості α і знаходиться за формулою:

,

де 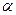− рівень значущості; − число степенів вільності; 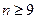− обсяг вибірки; − критична точка розподілу Стьюдента для двосторонньої критичної області (див. додаток 3).

Якщо , то зв’язок вважається істотним з імовірністю γ=( 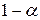) і навпаки. Рівень значущості 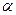зазвичай вибирається рівним 0,05 або 0,10 і являє собою імовірність ризику визнати зв’язок істотним, коли він насправді не існує.

Якщо зв’язок буде визнано істотним, то його щільність можна оцінювати за правилом трисекції:

– для (0,3 + 0,7; 1] зв’язок вважаємо щільним;

– для (0,7 + 0,3; 0,3 + 0,7] – помірним;

– для ( ; 0,7 + 0,3] – слабким.

Знак визначає напрям залежності: якщо , то зв’язок прямий і навпаки.

Читайте також:

1. B. Тип, структура, зміст уроку і методика його проведення.
2. D) методу мозкового штурму.
3. Demo 11: Access Methods (методи доступу)
4. H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
5. I Метод Шеннона-Фано
6. I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
7. I. Метод єдиної подібності.
8. I. Метод рiвних вiдрiзкiв.
9. II. МЕТОДИЧНІ ВКАЗІВКИ
10. II. УЧЕБНЫЕ И МЕТОДИЧЕСКИЕ ПОСОБИЯ, ПРАКТИКУМЫ
11. IV. КЕРІВНИЦТВО, КОНТРОЛЬ І НАДАННЯ ОРГАНІЗАЦІЙНО-МЕТОДИЧНОЇ ДОПОМОГИ ПРАКТИКАНТАМ.
12. IV. Метод супутних змін.

Переглядів: 576