Аналітичне вирівнювання рядів динаміки

Аналітичне вирівнювання є більш досконалим способом обробки часових рядів, який дає можливість не тільки гарантовано (хоча інколи й не дуже надійно) виявляти тенденцію та її характер, але й робити прогноз розвитку явища на наступні часові моменти або інтервали. Метод застосовний для рівномірних інтервальних рядів і для моментних рядів з довільними проміжками δ_і часу між моментами.

Суть методу полягає в тому, що кожний фактичний рівень у_і ознаки Y розглядається як сума двох доданків: 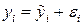, де 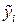– систематична складова, яка відображає загальну тенденцію і виражається рівнянням 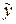=f(t); 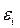– випадкова складова, яка відображає флуктуації рівнів ряду і завуальовує загальну тенденцію.

Таким чином, аналітичне вирівнювання динамічного ряду означає побудову функції 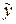=f(t), яка аналітично виражає залежність систематичної складової значень ознаки Y від часу t. При цьому для інтервальних часових рядів аргумент t звичайно являє собою порядковий номер інтервалу. Нумерацію будемо починати з нуля.

Такі функції і їх графіки називають трендовими кривими. За допомогою трендової кривої завжди можна встановити тенденцію розвитку явища, її характер, а також зробити прогноз на наступні часові інтервали або моменти.

Процедура побудови трендової кривої складається з двох етапів: 1) вибір виду функції f(t); 2) обчислення параметрів вибраної функції.

З формально-математичної точки зору побудова трендової кривої цілком аналогічна побудові рівняння регресії, що детально розглядалось у п. 2.4 л. р. № 3, за винятком двох моментів:

1. Якщо ряд є рівномірним і неперервним, то системи лінійних алгебраїчних рівнянь (3.9), (3.10) можна суттєво спростити. Для цього необхідно: а) усі часові моменти t_i моментного ряду пронумерувати, починаючи з нуля, і надалі моменти t_i ототожнювати з їх номерами (як і часові інтервали для інтервального ряду): t_i=і, і= 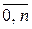; б) перейти до умовних номерів , перенумерувавши часові інтервали або моменти так, щоб точка відліку опинилась у середині часового ряду. Схематично це може виглядати, наприклад, так:

– для непарного числа (п+1) рівнів ряду: =t_i – п/2 (n=2l, ),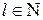

Фактичні номери t_i
Умовні номери	–2	–1

– для парного числа (п+1) рівнів ряду: =2t_i – п (n=2l+1, ),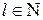

Фактичні номери t_i
Умовні номери	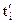–5	–3	–1

Очевидно, що 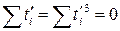, за рахунок чого і спрощуються системи рівнянь. Зокрема, система (3.9) для умовних параметрів а₁і b₁ набуває вигляду

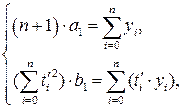(4.19)

звідки

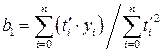, . (4.20)

Система (3.10) для умовних параметрів p₁, q₁i r₁ набуває вигляду

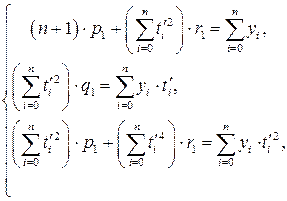(4.21)

звідки 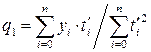, що збігається з відповідною формулою (4.20), а параметри p₁ i r₁ знаходяться як розв’язок системи двох лінійних рівнянь, що складається з першого і третього рівнянь системи (4.21).

Після розв’язання систем (4.19) і (4.21) одержуємо лінійну та квадратичну (або параболічну) моделі тренду відповідно

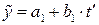та 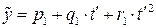, (4.22)

як функції умовного часу .

Для переходу до фактичного часу t необхідно в рівняннях (4.22) замість покласти: =t–l для непарного числа рівнів ряду, де l=n/2; =2t–п для парного числа рівнів ряду. В результаті одержимо лінійну та квадратичну моделі тренду відповідно

та 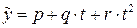, (4.23)

де a=a₁– b₁· l, b=b₁, p=p₁– q₁· l+r₁·l², q=q₁– 2r₁· l, r=r₁ для непарного числа (n+1); a=a₁– b₁· п, b=2b₁, p=p₁+ q₁· п+r₁· n², q=2q₁– 4r₁· n, r=4r₁ для парного числа (n+1).

2. Регресійна дисперсія обчислюється за формулою

, (4.24)

де 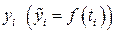– фактичні (вирівняні) значення рівнів ряду; (п+1) – число рівнів ряду; п – номер останнього рівня ряду, якщо нумерація починається з нуля; т – число параметрів трендової кривої.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Згладжування рядів динаміки	\|	Інтерполяція, екстраполяція та прогнозування часових рядів

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.092 сек.