• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Знаходження моди та медіани

Для обчислення моди та медіани необхідно спочатку знайти модальний та медіанний інтервали побудованого і. в. р.

Очевидно, що модальним є 4-й інтервал, оскільки його частота f₄=36 найбільша.

Для знаходження медіанного інтервалу необхідно для кожного і-го інтервалу знайти накопичену частоту S_i . Очевидно, що S₁=f₁ , а S_i+1= S_і +f_i+1 . Накопичені частоти будемо знаходити у діапазоні, наприклад Q4-Q10. Так S₅ знаходимо за формулою “=Q7+І8”, як показано на рис. 1.18.

Аналізуючи значення S_i, легко встановити, що медіанним інтервалом є 4-й інтервал, оскільки він перший з інтервалів, для яких накопичена частота перевищує половину обсягу сукупності: .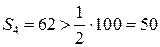

Після знаходження модального та медіанного інтервалів обчислюємо моду та медіану за відповідними формулами

, ,

округлюючи їх значення до двох десяткових знаків.

Рис. 1.18.

Для даного прикладу ці характеристики обчислюємо у комірках, наприклад, К15 та К16 за формулами відповідно

“ =ОКРУГЛ(G7+D5*((I7-I6)/(2*I7-I6-I8));2)”

“ =ОКРУГЛ(G7+D5*((D10/2-I6)/I7);2)”, як показано на рис. 1.19.

Рис. 1.19.

За результатами дослідження можна зробити висновок: маємо одновершинний унімодальний гостроверхий (Ex>3) розподіл однорідної статистичної сукупності з незначною лівосторонньою асиметрією.

Читайте також:

1. Алгоритм знаходження ДДНФ (ДКНФ) для даної булевої функції
2. Алгоритм знаходження найбільшого та найменшого
3. Алгоритм знаходження оптимального плану
4. Алгоритм знаходження початкового опорного плану
5. Виведення формул для знаходження площі паралелограма, трикутника, трапеції. Формули для знаходження площ поверхонь просторових геометричних фігур.
6. Відомості про складову частину документу // Відомості про документ, у якому міститься складова. – Відомості про місцезнаходження складової у документі. – Примітки.
7. Ділення числа на те саме число, ділення на 1. Ділення 0 на число. Розв'язання задач на знаходження невідомих доданків за відомими сумами двох і трьох доданків.
8. Завдання 7. Методи знаходження точки беззбитковості, обсягу виробництва і прибутку
9. Задачі на знаходження невідомого за двома різницями
10. Задачі на знаходження частини (дробу) від числа та числа за поданою частиною (дробом)
11. Задачі на знаходження четвертого пропорційного
12. Знаходження кількості та ширини інтервалів

Переглядів: 414