Похибка вибірки

Якщо генеральна сукупність містить N елементів, а для обстеження потрібно вибрати з них частину n, то число можливих вибірок

Усі вони мають однакову ймовірність , але кожна з них несе в собі певну похибку, що відбиває факт випадковості вибору. Оскільки вибіркова сукупність не точно відтворює склад генеральної сукупності, то й вибіркові оцінки не збігаються з відповідними характеристиками генеральної сукупності. Розбіжності між ними називають похибками репрезентативності: для середньої — це різниця між генеральною та вибірковою середніми, для частки — різниця між генеральною і вибірковою р частками, для дисперсії — відношення генеральної 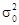та вибіркової дисперсій тощо.

За причинами виникнення похибки репрезентативностіподіляються на тенденційні(систематичні) та випадкові. Тенденційні похибки виникають, коли при формуванні вибіркової сукупності порушений принцип випадковості (упереджений вибір елементів, недосконала основа вибірки тощо). Ці похибки для всіх елементів сукупності однонапрямлені і призводять до зсунення результатів обстеження.

Випадкові похибки — це наслідок випадковості вибору елементів для дослідження і пов’язаних з цим розбіжностей між структурами вибіркової та генеральної сукупностей щодо ознак, які вивчаються.

При організації вибіркового обстеження важливо уникнути тенденційних похибок. Незсуненість — одна з вимог до будь-якої вибіркової оцінки. Притаманних вибірковому спостереженню випадкових похибок уникнути неможливо, проте теорія вибіркового методу дає математичну основу для обчислення таких похибок та регулювання їх розміру.

Згідно з генеральною граничною теоремою за умови достатньо великого обсягу вибірки розподіл вибіркових середніх (і часток), незалежно від розподілу генеральної сукупності, асимптотично наближається до нормального. Більшість значень вибіркових середніх зосереджується навколо генеральної середньої, а отже, найбільшу ймовірність мають відхилення, близькі до нуля. Чим більше відхилення, тим менша його ймовірність. Для будь-якої ймовірності існує межа відхилень вибіркової середньої від генеральної. Використовуючи властивості нормального розподілу, для однієї конкретної вибірки можна визначити:

· похибки репрезентативності — середню та граничну для взятої ймовірності;

· імовірність того, що похибка вибірки не перевищить допустимого рівня;

· обсяг вибірки, який забезпечить потрібну точність результатів для взятої ймовірності.

Кінцева мета будь-якого вибіркового спостереження — поширення його характеристик на генеральну сукупність. Для середньої та частки визначаються межі можливих їх значень у генеральній сукупності з певною ймовірністю — довірчі межі. Якщо метою вибіркового обстеження є визначення обсягових показників генеральної сукупності — обсягів значень ознаки , то вибіркова середня поширюється на генеральну сукупність прямим перерахунком: .

Наприклад, загальна посівна площа під круп’яними культурами в районі становить 2000 га. За даними вибіркового обстеження середня врожайність круп’яних культур — 22,5 ц/га, похибка середньої — 0,5 ц/га. Отже, можливий обсяг валового збору зерна з цієї площі буде не менший за 44 тис. ц [(2000 (22,5 – 0,5)]. Максимальний валовий збір — 46 тис. ц [(2000 (22,5 + 0,5)].

коли вибіркове спостереження проводиться з метою уточнення результатів суцільного спостереження, застосовується метод коефіцієнтів. Наприклад, після щорічного перепису худоби, що належить населенню, проводиться 10%-ний вибірковий контроль, мета якого — визначити частку недообліку худоби. За даними перепису в районі налічується 10000 корів. У домогосподарствах, які потрапили до контрольної вибірки, за переписом 200 корів, а за даними перевірки — 205. Отже, частка недообліку корів становить . Це і є той коефіцієнт, на який слід скоригувати результати перепису: 10000  1,025 = 10250 корів.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Генеральна первинна сукупність	\|	Систематичні (див. пит. 77)

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.016 сек.