СТАТИСТИЧНА ОБРОБКА РЕЗУЛЬТАТІВ ВИМІРЮВАННЯ

Мета заняття - прищеплення практичних навичок у галузі обробки результатів вимірювання.

Для успішного виконання завдань цього розділу необхідно знати:

• сутність точкового та інтервального оцінювання істинного значення вимірюваної величини;

• метод розрахунку математичного сподівання на основі багаторазових спостережень;

• метод розрахунку величини випадкової похибки на основі багаторазових спостережень;

• правила запису інтервальної оцінки.

З метою підвищення точності вимірювання, а також оцінювання випадкової похибки часто застосовують метод багаторазових спостережень. При цьому декілька разів вимірюють одну й ту ж саму фізичну величину, внаслідок чого випадкові похибки, так би мовити, взаємно компенсують одна одну: що більше спостережень, то ближче результат вимірювання до істинного значення величини і менше випадкова похибка (на жаль, систематичну похибку таким способом зменшити неможливо).

На основі багаторазових спостережень визначають точкову та інтервальну оцінки істинного значення вимірюваної величини.

Точкова оцінка, яка і є дійсним значенням величини, - це середнє арифметичне результатів усіх виконаних спостережень (математичне сподівання):

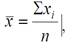, (1.1)

де xi – результат і-го виміру;

n – загальна кількість вимірів.

Точкова оцінка не дає жодної інформації про точність вимірювання або його похибку.

Щоб дати інтервальну оцінку, треба спочатку розрахувати середньоквадра-тичне відхилення

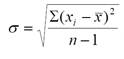. (1.2)

Імовірну випадкову похибку можна розрахувати за формулою

(1.3)

де t –критерій Стьюдента.

Величину критерію Стьюдента знаходять із таблиці розподілу Стьюдента (додаток А) в залежності від двох аргументів: 1) кількості ступенів свободи f = n – 1; 2) довірчої ймовірності р або рівня значущості a = 1 – р. Рівень значущості задає сам дослідник. Що менше цей рівень (більше довірча ймовірність), то менше точність, але більше надійність оцінки. У технічних вимірюваннях найчастіше беруть р = 0,95 (a = 0,05). Критерій Стьюдента має різне значення в залежності від того двобічне або однобічне обмеження має вимірювана величина. Наприклад, якщо згідно з стандартом вміст вуглецю в чавуні повинен знаходитись у межах від 2,8 до 3,2%, обмеження двобічне, якщо вміст сірки в сталі не повинен перевищувати 0,03% - однобічне.

Визначивши абсолютну похибку, можна записати інтервальну оцінку величини х у вигляді x = x ± Dx з імовірністю р. Межі, у яких знаходиться істинне значення величини, називають довірчим інтервалом.

Завдання 3.1. Дати точкову та інтервальну оцінку величини х, виходячи з такого ряду її спостережень: 1,00; 1,01; 1,00; 1,02; 0,98; 0,99. Довірчу ймовірність взяти рівною 0,95. Знайти відносну похибку вимірювання.

Розв’язання. Подібні задачі зручно розв’язувати, використовуючи таку таблицю:

Визначимо відхилення кожного виміру від середнього значення і запишемо (без знаку) у другу колонку. Піднесемо ці числа в квадрат (остання колонка) і просумуємо.

Визначимо середньоквадратичне відхилення

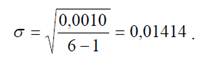
Далі, виходячи з кількості ступенів свободи f = 6 – 1 = 5 і рівня значущості a = 1 – 0,95 = 0,05, знайдемо в таблиці (додаток А) величину критерію Стьюдента (для двобічного обмеження) t = 2,57.

Розрахуємо ймовірну абсолютну похибку:

Для самостійної роботи: дати точкову та інтервальну оцінку істинного значення величини х (довірча ймовірність вказана в дужках):

а) 0,030; 0,028; 0,031 (0,95);

б) 1285; 1291; 1280; 1280; 1284 (0,9);

в) 1,25; 1,20; 1,26; 1,24; 1,22; 1,25; 1,25 (0,99).

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Індивідуальне завдання	\|	Індивідуальне завдання

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.019 сек.