• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Бульові функції

Загальна таблиця відповідності для бульових функцій однієї змінної має наступний вигляд:

Таблиця 2.1. Бульові функції однієї змінної

x			Позначення	Назва
y0				Константа 0
y1			x	Повторення аргументу
y2				Заперечення
y3				Константа 1

Тут дві функції y₀ =0 і y₃ =1 являють собою функції-константи (тотожний нуль і тотожна одиниця), оскільки вони не змінюють свого значення при зміні аргументу. Функція y₁ = x повторює значення змінної x і тому просто збігається з нею.

Таблиця 2.2. Бульові функції двох змінних

x1					Позначення	Назва функції
x2
y0						Константа 0
y1						Кон’юнкція
y2						Заперечення імплікації
y3		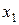				Повторення першого аргументу
y4						Заперечення оберненої імплікації
y5		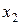				Повторення другого аргументу
y6						Сума по модулю 2
y7						Диз’юнкція
y8						Стрілка Пірса
y9		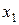			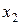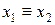~ ( )	Еквіваленція
y10		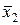				Заперечення другого аргументу
y11		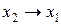				Обернена імплікація
y12						Заперечення першого аргументу
y13		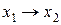				Імплікація
y14		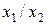				Штрих Шеффера
y15						Константа 1

Єдиною нетривіальною функцією є , яка називається запереченням (читається “не Ix”). Вона дорівнює 1, коли аргумент набуває значення 0, і дорівнює 0 при аргументі 1.

Всі 16 функцій двох змінних наведені в табл. 2.2, де вказані умовні позначення та назви функцій.

Множина всіх бульових функцій разом з операціями заперечення, кон’юнкції і диз’юнкції утворюють бульову алгебру.

На основі означення основних операцій неважко переконатися в справедливості наступних тотожностей (властивостей) бульової алгебри:

1. Закони комутативностіxÚy = yÚ;xy = yx;

2. Закони асоціативності (xÚy)Úz = xÚ(yÚz); (xy)z=x(yz).

3. Закони дистрибутивностіx(yÚz) = xyÚxz; xÚ(yz) = (xÚy)(xÚz).

4. Закони ідемпотентності xÚx = x; xx = x.

5. Закони де Моргана ; .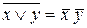

6. Закони поглинання xÚ(xy) = x; x(xÚy) = x.

7. Закони склеювання .

8. Закони, що містять 0 або 1:

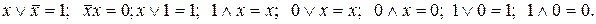
Приклад 1. Спростити формулу

.

Розв’язання. Застосуємо формули 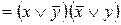, , закони дистрибутивності і де Моргана та формули xx =x, і . Одержимо

.

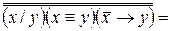
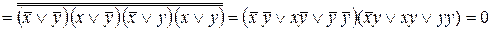Диз’юнктивна (кон’юнктивна) нормальна форма − це диз’юнкція (кон’юнкція) скінченного числа різних членів, кожен із яких являє собою кон’юнкцію (диз’юнкцію) окремих змінних або їх заперечень, які входять в даний член не більше одного разу.

Задана формула зводиться до нормальної форми наступним чином:

1) за допомогою законів де Моргана формула перетворюється до такого вигляду, щоб знаки заперечень відносились тільки до окремих змінних;

2) на основі першого (другого) дистрибутивних законів формула зводиться до диз’юнкції кон’юнкцій (кон’юнкції диз’юнкцій);

3) одержаний вираз спрощується у відповідності з тотожностями xx = x 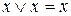і ( і ).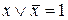

Якщо початкова формула містить інші операції, то вони попередньо виражаються через диз’юнкцію, кон’юнкцію і заперечення.

Якщо в кожному члені нормальної форми представлені всі змінні (в прямому чи інверсному вигляді), то вона називається досконалою нормальною формою. Якщо який-небудь член j диз’юнктивної (кон’юнктивної) нормальної форми не містить змінної x_i, то вона вводиться тотожним перетворенням 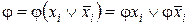(відповідно ). В силу тотожностей j Ú j =j і jj = j однакові члени, якщо вони з’являються, замінюються одним таким членом.

Для сукупності змінних x₁, x₂,…, x_n вираз називається конституентою одиниці, а вираз 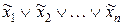− конституентою нуля ( означає x_i або ). Дана конституента одиниці (нуля) набуває значення одиниця (нуль) тільки при одному відповідному їй наборі значень змінних, який одержимо, якщо всі змінні приймемо рівними одиниці (нулю), а їх заперечення нулю (одиниці). Наприклад, конституенті одиниці 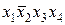відповідає набір (1011), а конституенті нуля − набір (1001).

Оскільки досконала диз’юнктивна (кон’юнктивна) нормальна форма є диз’юнкцією (кон’юнкцією) конституент одиниці (нуля), то можна стверджувати, що бульова функція f(x₁, x₂,…, x_n), яку вона представляє набуває значення одиниця (нуль) лише при наборах значень змінних x₁, x₂,…, x_n, які відповідають цим конституентам. На всіх інших наборах значень ця функція набуває значення нуль (одиниця).

Справедливе і обернене твердження, на якому оснований спосіб подання у вигляді формули функції, заданої таблицею відповідності. Для цього необхідно записати диз’юнкції (кон’юнкції) конституент одиниці (нуля), які відповідають наборам значень змінних, на яких функція набуває значення, рівного одиниці (нулю).

Інша важлива алгебра бульових функцій – алгебра Жегалкіна – будується на основі операцій додавання по модулю 2 і кон’юнкції. Справедливі наступні співвідношення:

.

Перші дві тотожності дозволяють перейти від будь-якої формули бульової алгебри до відповідної формули алгебри Жегалкіна, а за допомогою третьої тотожності здійснюється зворотній перехід.

Через операції алгебри Жегалкіна можна виразити всі інші бульові функції:

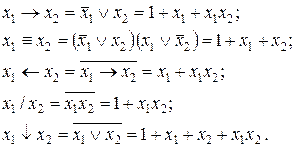
Будь-яка бульова функція зводиться до канонічного многочлена, члени якого не мають числових коефіцієнтів (відмінних від 0 і 1) і лінійні відносно будь-якої із змінних (змінні входять тільки в першому степені).

Розрізняють наступні типи бульових функцій:

1) Функції, які зберігають константу 0, тобто такі f(x₁, x₂,…, x_n), що f(0, 0,…,0) = 0.

2) Функції, які зберігають константу 1, тобто такі f(x₁, x₂,…, x_n), що f(1, 1,…,1) = 1.

3) Самодвоїсті функції, тобто такі, які набувають протилежних значень на будь-яких двох протилежних наборах значень змінних.

4) Лінійні функції, тобто такі, які в алгебрі Жегалкіна подаються канонічним многочленом, який не містить добутків змінних.

5) Монотонні функції, тобто такі, які для будь-яких двох наборів значень змінних, частково упорядкованих співвідношенням при , задовольняють нерівність

.

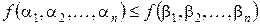Система функцій, суперпозицією яких може бути подана будь-яка функція із деякої множини бульових функцій, називається функціонально повною. Загальне вирішення питання основане на теоремі про функціональну повноту (теоремі Поста): для того щоб система бульових функцій була повною, необхідно і достатньо, щоб вона включала хоч би одну функцію: таку, що не зберігає константу 0, не зберігає константу 1, несамодвоїсту, нелінійну і немонотонну. Цю теорему слід розуміти так, що одна і та ж функція може представляти у функціонально повній системі одну або декілька необхідних властивостей, якщо вона ці властивості має.

В табл. 2.3 зірочкою відмічені властивості, які має дана функція.

Вибравши будь-яку елементарну функцію і доповнивши її однією чи кількома іншими функціями так, щоб вони всі разом задовольняли теорему Поста, можна виразити через них і всі інші функції.

Таблиця 2.3. Властивості бульових функцій

Бульова функція	Формули	Властивості
Незбереження 0	Незбереження 1	Несамодвоїстість	Нелінійність	Немонотонність
Константа 0
Константа 1
Заперечення
Кон’юнкція
Диз’юнкція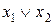
Імплікація
Еквіваленція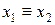
Заперечення імплікації
Сума по модулю 2
Штрих Шеффера
Стрілка Пірса

Питання для самоперевірки

1.Що таке бульові змінні?

2.Які є способи задання бульових функцій?

3.Які основні властивості бульових функцій?

4.Як формулюється принцип двоїстості?

5.Які є типи бульових функцій?

6.Дайте означення диз’юнктивної (кон’юнктивної) нормальної форми.

7.Дайте означення досконалої диз’юнктивної (кон’юнктивної) нормальної форми.

Література: [1], c. 29-33, 39-58; [2], c. 23-35.

Вправи

48. Написати таблиці відповідності для наступних бульових функцій:

.

49. Знайти значення кожної з даних бульових функцій

при x₁ = 1, x₂ = 0, x₃ =1, x₄ =1..

50. За допомогою таблиць відповідності переконайтесь в справедливості наступних рівносильностей:

51. Спростити вирази:

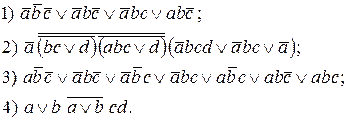
52. Чи еквівалентні формули і :

53. Перевірити справедливість співвідношень:

54. Перевірити рівносильності двома способами: побудувавши таблицю істинності і спростивши ліву та праву частини рівності:

;

;

;

;

;

.

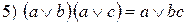55. Шляхом тотожних перетворень довести рівносильність

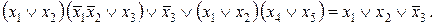
56. Звести до досконалої диз’юнктивної і кон’юнктивної нормальних форм функцію 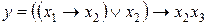: а)шляхом тотожних перетворень;

б) за допомогою таблиці відповідності.

57. Записати досконалі диз’юнктивні і кон’юнктивні нормальні форми функцій y₁ і y₂ трьох змінних x₁, x₂, x₃, заданих таблицею відповідності:

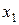
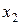
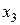
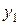
58. За допомогою еквівалентних перетворень звести до диз’юнктивної нормальної форми функції :

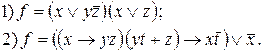
59. Представити у вигляді досконалої диз’юнктивної нормальної форми наступні функції:

60. Виразити через операції алгебри Жегалкіна наступні функції:

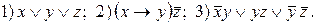
61. Показати, що функція лінійна.

62. Побудувати поліном Жегалкіна для функцій:

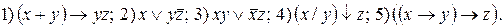
63.Чи є функція двоїстою до функції , якщо

64. Користуючись властивостями бульових функцій, вказати, які з наступних систем функцій являються функціонально повними:

а) імплікація і константа 0;

б) сума по модулю 2 і імплікація;

в) еквіваленція, заперечення і константа 0;

г) кон’юнкція, заперечення імплікації і константа 1;

д) диз’юнкція і еквіваленція;

е) диз’юнкція, сума по модулю 2 і заперечення.

Читайте також:

1. Автоматизоване робоче місце (АРМ) бухгалтера: призначення, функції та його рівні
2. Адвокатура в Україні: основні завдання і функції
3. Адміністративна відповідальність: поняття, мета, функції, принципи та ознаки.
4. Алгоритм знаходження ДДНФ (ДКНФ) для даної булевої функції
5. Але відмінні від значення функції в точці або значення не існує, то точка називається точкою усувного розриву функції .
6. Аналіз коефіцієнтів цільової функції
7. Апроксимуючий поліном функції відгуку
8. АРХІВНІ ДОВІДНИКИ В СИСТЕМІ НДА: ФУНКЦІЇ ТА СТРУКТУРА
9. АРХІВНІ ДОВІДНИКИ В СИСТЕМІ НДА: ФУНКЦІЇ ТА СТРУКТУРА
10. Асимптоти графіка функції
11. Асимптоти графіка функції
12. Базальні ядра, їх функції, симптоми ураження

Переглядів: 1735