• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Мінімізація логічних функцій

Мінімальною диз’юнктивною нормальною формою функції f називається диз’юнктивна нормальна форма, яка містить мінімально можливе число входжень символів змінних серед усіх диз’юнктивних нормальних форм, які реалізують функцію f. Задачі побудови мінімальних диз’юнктивних нормальних форм називаються задачами мінімізації .

Нехай дано дві логічні функції g(x₁,…, x_n) і f(x₁,…, x_n). Кажуть, що логічна функція g входить в логічну функцію f і пишуть g Ì f, якщо виконується наступна умова: на всіх наборах, на яких f дорівнює нулю, g також дорівнює нулю.

Будь-яка функція g(x₁,…, x_n), яка входить в дану функцію f(x₁,…, x_n), називається її імплікантом. Інакше, функція g(x₁,…, x_n) називається імплікантом функції f(x₁,…, x_n), якщо для будь-якого набору (a₁, …, a_n) значень аргументів виконується нерівність f(x₁,…, x_n) ³ g(x₁,…, x_n). Цю умову можна еквівалентно подати у вигляді f(x₁,…, x_n) g(x₁,…, x_n) 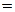g(x₁,…, x_n).

Імплікант називається простим, якщо він являє собою кон’юнкцію змінних (можливо із запереченнями), і будь-яка кон’юнкція, одержана з нього в результаті видалення яких-небудь змінних, імплікантом не являється. Щоб вияснити, чи є імплікант, який має вигляд кон’юнкції, простим, досить дослідити наявність імплікантів серед кон’юнкцій, одержаних видаленням з нього рівно однієї змінної.

Довести, що функці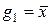ї і є імплікантами функції , можна також, переконавшись в справедливості співвідношень: .

В основі розв’язання задачі мінімізації логічних функцій лежить схема, яка містить два етапи: 1) відшукання всіх простих імплікантів функції f, тобто побудова її скороченої диз’юнктивної нормальної форми; 2) побудова тупикових (без зайвих імплікантів) диз’юнктивних нормальних форм з числа мінімальних.

Існують різні методи мінімізації логічних функцій.

Метод послідовного застосування законів і тотожностей алгебри логіки полягає в тому, що відшукуються вирази, кожен з яких можна представити в простішому вигляді:

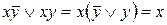(операція склеювання);

(операція поглинання);

(дистрибутивний закон).

При спрощенні завжди слід мати на увазі тотожність x Ú x = x, з якої випливає, що кожен доданок можна групувати з іншими неодноразово.

Перед початком спрощення логічна функція може бути представлена в довільній формі, що є перевагою методу. Однак цей метод використовується у відносно простих випадках, оскільки потребує певних навичок і містить елементи довільних розв’язань.

Метод Квайна. В методі Квайна прості імпліканти знаходяться по досконалій диз’юнктивній нормальній формі в результаті застосування до неї операції неповного склеювання і операції елементарного поглинання.

Метод Блейка дозволяє шукати прості імпліканти, використовуючи представлення функції в довільній диз’юнктивній нормальній формі, а також операцію узагальненого склеювання, яка описується виразом

.

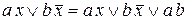Питання для самоперевірки

1.Що таке скорочена диз’юнктивна (кон’юнктивна) нормальна

форма?

2.Назвіть і охарактеризуйте методи, за якими утворюють мінімальні форми.

Література: [1], c. 58-74, 39-58; [2], c. 35-38.

Вправи

65. Методом послідовного застосування законів і тотожностей алгебри логіки знайти скорочену диз’юнктивну нормальну форму логічної функції: .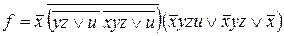

66. Методом Квайна знайти скорочену диз’юнктивну нормальну форму логічних функцій:

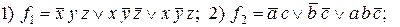3) ;

4) .

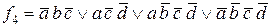67. Методом Блейка знайти скорочену диз’юнктивну нормальну форму логічних функцій:

;

.

Читайте також:

1. V. Етичні правила психологічних досліджень
2. V. Рекомендації щодо безпечного застосування сільськогосподарської техніки при виконанні основних агротехнологічних операцій у рослинництві
3. VI. Рекомендації щодо безпечного використання сільськогосподарської техніки при виконанні основних технологічних операцій у тваринництві
4. XV. Фінансові результати від первісного визнання та реалізації сільськогосподарської продукції та додаткових біологічних активів
5. АВТОМАТИЗАЦІЯ ТЕХНОЛОГІЧНИХ ПРОЦЕСІВ
6. АВТОМАТИЗАЦІЯ ТЕХНОЛОГІЧНИХ ПРОЦЕСІВ
7. Автоматизація технологічних процесів і транспортні засоби.
8. Аденогіпофіз, його гормони, механізм впливу, прояви гіпер- та гіпофункцій.
9. Актуальні смуги гідрологічних об’єктів та їх використання
10. Антенатальна профілактика стоматологічних захворювань
11. Аутентифікація з використанням односторонніх функцій
12. БЕЗПЕЧНІСТЬ ТЕХНОЛОГІЧНИХ ПРОЦЕСІВ

Переглядів: 2623