• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Оцінка точності вирівняних елементів мережі

Середня квадратична похибка вирівняної мережі обчислюється за формулою

,(2.23)

де середня квадратна похибка одиниці ваги обчислена за формулою

, (2.24)

де V – поправка з вирівнювання до виміряних з вагою Р напрямків;
r – число надлишкових вимірювань; – обернена вага вирівняного елементу.

До числа необхідних вимірювань при вирівнюванні мережі за напрямками відносяться: 1) поправки орієнтування , число яких рівне числу t пунктів, з яких велись спостереження; 2) поправки координат , – число яких дорівнює подвоєному числу К визначених пунктів. Так як всіх напрямків виміряно D, то

D – ( 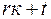). (2.25)

Якщо в мережі крім напрямків були виміряні додатково Кs сторін і Ка азимутів, то загальне число всіх виміряних величин

, (2.26)

а число надлишкових вимірювань визначається за формулою

. (2.27)

Для мережі, показаній на малюнку 2, в якій

D = 18, К = 3, t = 6,

отримаємо

;

.

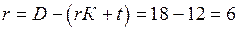Кожному напрямку надали вагу Р=1.

Середня квадратична похибка кута:

.

У випадку параметричного способу вимірювання простіше обчислюється вага останнього і передостаннього невідомих у системі нормальних рівнянь. Вага Р_ук останнього невідомого у випадку розв’язання системи нормальних рівнянь за схемою Гауса рівний коефіцієнту при в останньому перетвореному нормальному рівнянні. Вага Р_хк передостаннього невідомого знаходиться за формулою:

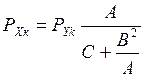, (2.28)

де С і А – квадратичні коефіцієнти відповідно останнього та передостаннього перетворених нормальних рівнянь; В – коефіцієнт при в передостанньому перетвореному рівнянні.

Середні квадратичні похибки визначення абсцис і ординат знайдемо за формулами:

; (2.29)

. (2.30)

Загальна погрішність положення пункту

, (2.31)

В табл. 2.11 визначені обернена вага довжини і дирекційного кута сторони КВ:

; .

За цими даними отримуємо:

_; .

Читайте також:

1. A) Оцінка захисних споруд за ємністю – визначення коефіцієнта Квм.
2. B) Оцінка ЗС за захисними властивостями
3. II. За зміною ступенів окиснення елементів, які входять до складу реагуючих речовин
4. IV. Загальна оцінка діяльності вчителя
5. IV. Оцінка вигідності залучення короткотермінових кредитів
6. IV. Оцінка привабливості стратегічних зон господарювання підприємства на ринку.
7. А) Грошова оцінка земель по Україні
8. А) Оцінка захисних споруд за місткістю – визначення коефіцієнта Квм
9. Абетка елементів поведінки тварини
10. Абонентський стик ISDN мережі
11. Автоматичне налагодження їх індуктивності на ємність мережі для забезпе1
12. Алгоритм розрахунку матриці найкоротших відстаней на ділянках мережі методом Флойда – Уоршелла

Переглядів: 360