Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Властивості математичного сподівання

1. Математичне сподівання від сталої величини С дорівнює самій сталій:

М (С) = С. (80)

Справді, сталу С можна розглядати як випадкову величину, що з імовірністю, яка дорівнює одиниці, набуває значення С, а тому
М (С) = С × 1 = С.

2.М (СХ) = СМ (Х). (81)

Для дискретної випадкової величини згідно із (75) маємо

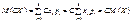Для неперервної:

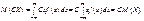
3. Якщо А і В є сталими величинами, то

. (82)

Для дискретної випадкової величини:

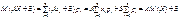Для неперервної випадкової величини:

Приклад 1. Закон розподілу дискретної випадкової величини задано таблицею:

х_і	– 6	– 4
р_і	0,1	0,1	0,2	0,3	0,1	0,2

Обчислити М (Х).Розв’язання. Скориставшись (76), дістанемо

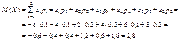Якщо випадкова величина Х Î [а; b], то М (Х) Î [а; b], а саме: математичне сподівання випадкової величини має обов’язково міститься всередині інтервалу [а; b], являючи собою центр розподілу цієї величини.

25. Мода та медіана випадкової величиниМодою (Мo) дискретної випадкової величини Х називають те її можливе значення, якому відповідає найбільша ймовірність появи.Модою для неперервної випадкової величини Х називають те її можливе значення, якому відповідає максимальне значення щільності ймовірності:f (Mо) = max.Якщо випадкова величина має одну моду, то такий розподіл імовірностей називають одномодальним; якщо розподіл має дві моди — двомодальним і т. ін. Існують і такі розподіли, які не мають моди. 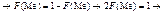Їх називають антимодальними.Медіаною (Ме) неперервної випадкової величини Х називають те її значення, для якого виконуються рівність імовірностей подій: (83)Отже, медіану визначають із рівняння (83).Приклад 5. Робітник під час роботи обслуговує три верстати-автомати. Імовірність того, що верстат-автомат потребує уваги робітника за певний проміжок часу, — величина стала і дорівнює 0,8.Побудувати закон розподілу ймовірностей дискретної випадкової величини Х — числа верстатів, які потребують уваги робітника за певний проміжок часу. Знайти Мо.Розв’язання. Можливі значення випадкової величини:Х = 0, 1, 2, 3.Імовірності цих можливих значень такі:p₁ = (0,2)³ = 0,008;p₂ = 3р q² = 3 × 0,8 × 0,04 = 0,096;p₃ = 3p²q = 3 × 0,64 × 0,2 = 0,384;p₄ = p³ = (0,8)³ = 0,512.Запишемо закон таблицею:

х_і
р_і	0,008	0,096	0,384	0,512

Із таблиці визначаємо Мo = 3.Отже, дістаємо одномодальний розподіл.Ме— можливе значення випадкової величини Х, причому таке, що пряма, проведена перпендикулярно до відповідної точки на площині Х = Ме, поділяє площу фігури, яка обмежена функцією f (x), на дві рівні частини.

26. Дисперсія та середнє
квадратичне відхилення

Математичне сподівання не дає достатньо повної інформації про випадкову величину, оскільки одному й тому самому значенню М (Х) може відповідати безліч випадкових величин, які будуть різнитися не лише можливими значеннями, а й характером розподілу і самою природою можливих значень.

Приклад 7. Закони розподілу випадкових величин Х і Y задані таблицями:

х_і	– 0,5	– 0,1	0,1	0,5
р_і	0,4	0,1	0,1	0,4

у_j	– 100	– 80	– 10
p_j	0,1	0,2	0,2	0,2	0,1	0,2

х_і	– 0,5	– 0,1	0,1	0,5
р_і	0,4	0,1	0,1	0,4

у_j	– 100	– 80	– 10
p_j	0,1	0,2	0,2	0,2	0,1	0,2

Обчислити М (Х) і М (Y).

Розв’язання.

Отже, два закони розподілу мають однакові математичні сподівання, хоча можливі значення для випадкових величин Х і Y істотно різні. Із наведеного прикладу бачимо, що в разі рівності математичних сподівань (М (X) = М (Y) = 0) випадкові величини Х і Y мають тенденцію до коливань відносно М (X) та М (Y), причому Y має більший розмах розсіювання відносно М (Y), ніж випадкова величина Х відносно М (Х). Тому математичне сподівання називають центром розсіювання. Для вимірювання розсіювання вводиться числова характеристика, яку називають дисперсією.

Для визначення дисперсії розглядається відхилення випадкової величини Х від свого математичного сподівання (Х – М (Х))

Математичне сподівання такого відхилення випадкової величини Х завжди дорівнює нулю. Справді,

Отже, відхилення не може бути мірою розсіювання випадкової величини.

Дисперсією випадкової величини Х називається математичне сподівання квадрата відхилення цієї величини

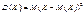. (86)

Для дискретної випадкової величини Х дисперсія

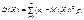; (87)

для неперервної

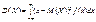. (88)

Якщо Х Î [а; b],

то 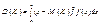. (89)

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Математичне сподівання	\|	Властивості дисперсії

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.