
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Вказівки до виконання контрольної роботи ( РГР ).
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
Запорізький національний технічний університет
МЕТОДИЧНІ ВКАЗІВКИ
до виконання контрольних робіт
(для студентів заочної форми навчання)
та РГР (для студентів денної форми
навчання) з вищої математики
(прискорена форма навчання)
( 1 семестр, 2 частина)
| |
( 1 семестр, 2 частина)
/ Укл. : Килимник І.М., Онуфрієнко Л.М., Полякова Т.Г. - Запоріжжя: ЗНТУ, 2014 -82 с.
Укладачі: Килимник І.М., к.т.н., доцент, Онуфрієнко Л.М., к. ф.-м. н, доцент, Полякова Т.Г. асистент
Комп’ютерна верстка: Давиденко С.І.
Відповідальний за випуск: Килимник І.М., к.т.н.,доцент
Затверджено на засіданні кафедри вищої математики ЗНТУ. Протокол № 2 від 03.09.2014
ЗМІСТ
Правила оформлення та виконання контрольної роботи (РГР) 4
1. Контрольна робота (РГР) № 2. Невизначений та визначений інтеграли. Подвійний інтеграл. Криволінійні інтеграли. Теорія поля. 5
1.1 Вказівки до виконання контрольної роботи ( РГР ) 5
1.1.1 Невизначений інтеграл 5
1.1.2Визначений інтеграл 19
1.1.3 Подвійний інтеграл 39
1.1.4 Потрійний інтеграл 53
1.1.5 Криволінійні інтеграли 58
1.1.6 Елементи теорії поля 65
1.2 Індивідуальні завдання 82
Література 118
Правила оформлення та виконання контрольної роботи (РГР)
1.Студент повинен виконувати контрольну роботу (РГР) в окремому зошиті.
2. На обкладинці зошита треба записати номер контрольної роботи (РГР), назву дисципліни, з якої виконується контрольна робота (РГР), номер академічної групи, прізвище, ім’я по батькові повністю. В правому верхньому куті вказати шифр – номер залікової книжки.
3. В контрольній роботі (РГР) повинні бути розв’язані всі завдання, вказані викладачем. Розв’язання завдань необхідно записувати в порядку номерів завдань, зберігаючи їх послідовність. Умова задачі в завданні переписується повністю.
4. Номер задачі в завданні вибирають таким чином: дві останні цифри шифру треба поділити на 30. Остача від ділення відповідає номеру задачі в завданні.
Якщо остача дорівнює нулю, то студент розв’язує 30 задачу завдання.
5. Контрольна робота (РГР) подається викладачеві на перевірку і захищається студентом на консультаціях. Контрольна робота (РГР), виконана не за своїм варіантом, не зараховується.
Контрольна робота ( РГР ) № 2
Невизначений та визначений інтеграли. Подвійний інтеграл. Криволінійні інтеграли. Теорія поля.
Вказівки до виконання контрольної роботи ( РГР ).
1.1.1 Невизначений інтеграл.
Функція  називається первісною для функції
називається первісною для функції 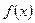 на проміжку
на проміжку  , якщо
, якщо  диференційована на
диференційована на  і справджується рівність
і справджується рівність 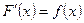 для усіх
для усіх 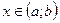 . Існує множина первісних
. Існує множина первісних  для функції
для функції 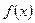 , які відрізняються тільки сталою:
, які відрізняються тільки сталою: 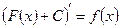 . Цю множину первісних називають невизначеним інтегралом функції
. Цю множину первісних називають невизначеним інтегралом функції 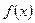 і записують
і записують 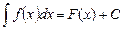 , де
, де 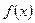 – підінтегральна функція.
– підінтегральна функція.
Властивості невизначеного інтеграла
а) 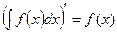
б) 
в) 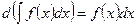
г) 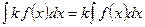 , де
, де  const
const
д) 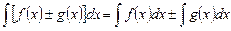
е) 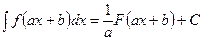
Таблиця невизначених інтегралів 
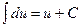
| 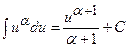 ; ; 
| ||
| 2a | 
| 
| |
| 2б | 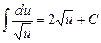
| 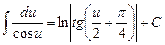
| |
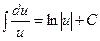
| 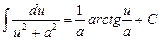
| ||
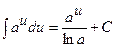
| 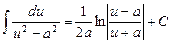
| ||
| 4а | 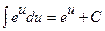
| 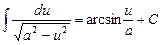
| |
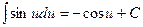
| 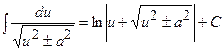
| ||
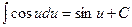
|  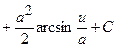
| ||

| 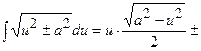 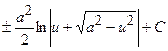
| ||
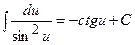
| 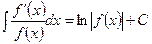
| ||
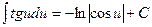
| 
| ||
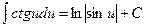
|
Зауваження: таблицею інтегралів можна користуватись у випадку, коли аргумент підінтегральної функції і вираз під знаком диференціала однакові.
Методи інтегрування
а) метод безпосереднього інтегрування. Обчислення інтегралів за допомогою властивостей невизначеного інтеграла та таблиці невизначених інтегралів.
Треба пам’ятати , що 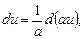
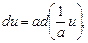
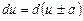 , де
, де  .
.
Задача 1. Знайти інтеграли
1) 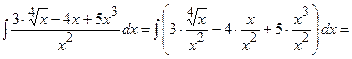
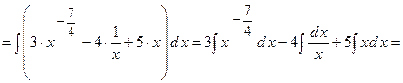
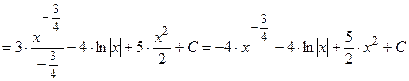 ;
;
2)  . Можемо застосувати формулу 2б, де
. Можемо застосувати формулу 2б, де  , і врахуємо лінійність аргументу u. За властивістю е) коефіцієнт лінійності дорівнює 3. Матимемо:
, і врахуємо лінійність аргументу u. За властивістю е) коефіцієнт лінійності дорівнює 3. Матимемо:  ;
;
3)  . Аналогічно прикладу 2), коефіцієнт лінійності дорівнює 7. Застосовуємо формулу 4а. Матимемо:
. Аналогічно прикладу 2), коефіцієнт лінійності дорівнює 7. Застосовуємо формулу 4а. Матимемо:
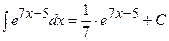 ;
;
4) 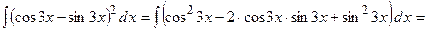
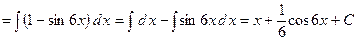 .
.
При знаходженні інтеграла врахували, що  і
і 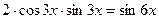
б) метод заміни змінної (метод підстановки). Згідно цього метода вводять нову змінну інтегрування. Нехай  – первісна функції
– первісна функції 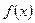 на проміжку
на проміжку  . Функція
. Функція  визначена та диференційована на проміжку
визначена та диференційована на проміжку  і
і 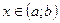 . Тоді справедлива формула
. Тоді справедлива формула 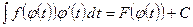 . Зручним є і такий запис:
. Зручним є і такий запис: 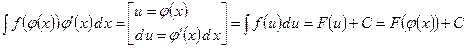 Підстановку
Підстановку  підбирають так, щоб мати після перетворення табличний інтеграл.
підбирають так, щоб мати після перетворення табличний інтеграл.
Задача 2. Знайти інтеграли
1) 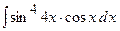
Так як 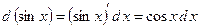 , то зробимо заміну змінної
, то зробимо заміну змінної  . Матимемо:
. Матимемо:
 . Перевіримо отриманий результат:
. Перевіримо отриманий результат:
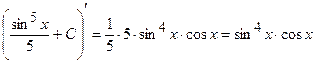 .
.
2) 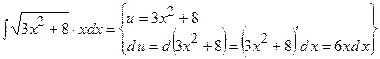 =
=
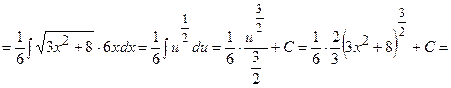
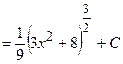 .
.
3) 
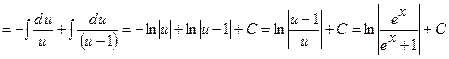
в) метод інтегрування частинами. Формула інтегрування частинами має вигляд:  . До інтегралів, які обчислюються методом інтегрування частинами відносяться:
. До інтегралів, які обчислюються методом інтегрування частинами відносяться:
1)  ,
, 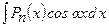 ,
, 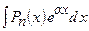 ,
, 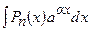 , де
, де  – многочлен
– многочлен 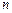 -го степеня,
-го степеня,  – дійсне число. В цих інтегралах через
– дійсне число. В цих інтегралах через 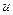 позначаємо
позначаємо  , а через
, а через 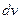 – один з виразів
– один з виразів 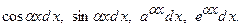
2) 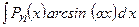 ,
, 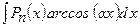 ,
, 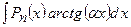 ,
, 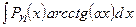 ,
, 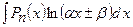 ,
,  , де
, де  – многочлен
– многочлен 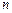 -го степеня (
-го степеня ( 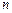 може дорівнювати нулю),
може дорівнювати нулю), 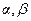 – дійсні числа. В цих інтегралах через
– дійсні числа. В цих інтегралах через 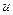 позначаємо один з виразів
позначаємо один з виразів 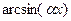 ,
, 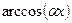 ,
,  ,
, 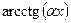 ,
, 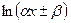 ,
,  , а через
, а через 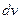 –
– 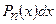 .
.
Існують інші типи інтегралів для знаходження яких застосовують метод інтегрування частинами.
Зауваження. При застосуванні метода інтегрування частинами треба підінтегральний вираз розбити на два множники: u і  , а саме: 1)
, а саме: 1) 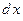 треба віднести до
треба віднести до 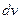 ; 2)
; 2) 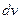 повинен бути таким, щоб інтегруванням легко знайти
повинен бути таким, щоб інтегруванням легко знайти  ; 3) Інколи доводиться формулу інтегрування частинами застосовувати декілька разів.
; 3) Інколи доводиться формулу інтегрування частинами застосовувати декілька разів.
Задача 3. Знайти інтеграли
1) 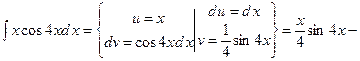
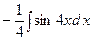
 ;
;
2) 
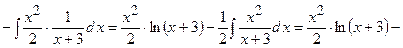

3) 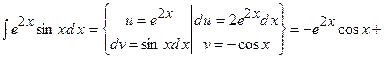

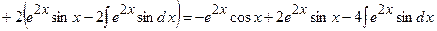
Розв’яжемо отримане рівняння відносно шуканого інтеграла
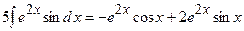
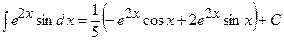
г) інтегрування квадратних тричленів. До цих інтегралів відносяться:
1) 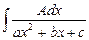 , 2)
, 2) 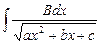 , 3)
, 3) 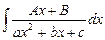 ,
,
4)  . Для інтегралів 1), 2) типів необхідно виділити повний квадрат у квадратному тричлені:
. Для інтегралів 1), 2) типів необхідно виділити повний квадрат у квадратному тричлені:

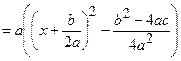 . Заміна
. Заміна 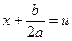 приводить інтеграл до табличного: для інтеграла 1) типу маємо табличний інтеграл 13 або 14, для інтеграла 2) типу маємо табличний інтеграл 15 або 16. Для інтегралів 3), 4) типів необхідно у чисельнику виділити похідну квадратного тричлена, який знаходиться у знаменнику, і чисельник почленно поділити на знаменник. Отримаємо два інтеграли, перший з яких знаходимо по таблиці інтегралів за формулою 17 ( для інтеграла 3) типу ) або 18 ( для інтеграла 4) типу ). Другий інтеграл є інтегралом 1) або 2) типу.
приводить інтеграл до табличного: для інтеграла 1) типу маємо табличний інтеграл 13 або 14, для інтеграла 2) типу маємо табличний інтеграл 15 або 16. Для інтегралів 3), 4) типів необхідно у чисельнику виділити похідну квадратного тричлена, який знаходиться у знаменнику, і чисельник почленно поділити на знаменник. Отримаємо два інтеграли, перший з яких знаходимо по таблиці інтегралів за формулою 17 ( для інтеграла 3) типу ) або 18 ( для інтеграла 4) типу ). Другий інтеграл є інтегралом 1) або 2) типу.
Задача 4. Знайти інтеграл

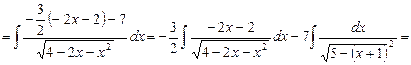

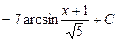
д) інтегрування дробово-раціональних функцій. До цих функцій
відносяться дроби  . Якщо
. Якщо 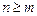 , то дріб є неправильний. Треба виділити цілу частину, поділивши чисельник на знаменник:
, то дріб є неправильний. Треба виділити цілу частину, поділивши чисельник на знаменник: 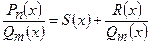 , де
, де  – частка (ціла частина),
– частка (ціла частина),  – правильний дріб (степінь многочлена
– правильний дріб (степінь многочлена 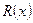 менший за
менший за 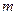 ). Далі, якщо правильний дріб не є простий, необхідно знаменник
). Далі, якщо правильний дріб не є простий, необхідно знаменник  розкласти на множники (множниками можуть бути многочлени виду:
розкласти на множники (множниками можуть бути многочлени виду: 
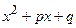 ,
, 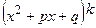 з дискримінантом квадратного тричлена меншим нуля), потім правильний дріб – на прості дроби. Простих дробів буде стільки, скільки множників у знаменнику, враховуючи кратність кожного. У чисельниках простих дробів записують многочлени в загальному вигляді, не враховуючи кратність многочленів у знаменнику. Коефіцієнти чисельників знаходимо методом невизначених коефіцієнтів або комбінованим методом. При інтегруванні правильних простих дробів можемо мати такі інтеграли:
з дискримінантом квадратного тричлена меншим нуля), потім правильний дріб – на прості дроби. Простих дробів буде стільки, скільки множників у знаменнику, враховуючи кратність кожного. У чисельниках простих дробів записують многочлени в загальному вигляді, не враховуючи кратність многочленів у знаменнику. Коефіцієнти чисельників знаходимо методом невизначених коефіцієнтів або комбінованим методом. При інтегруванні правильних простих дробів можемо мати такі інтеграли:
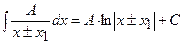 ;
;
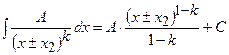 ;
;
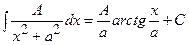 ;
;
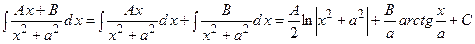
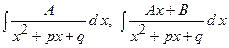 – розглянуті в інтегруванні квадратних тричленів;
– розглянуті в інтегруванні квадратних тричленів;

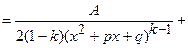
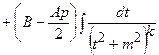 , де
, де 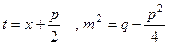 . При цьому многочлен
. При цьому многочлен 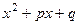 немає дійсних коренів, тобто
немає дійсних коренів, тобто  ;
;
 можна знайти використовуючи рекурентну формулу:
можна знайти використовуючи рекурентну формулу: 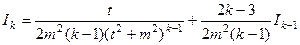
Задача 5. Знайти інтеграли
1) 
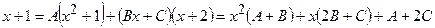

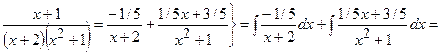
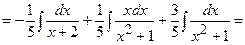
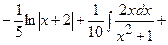

 ;
;
2) 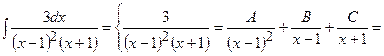
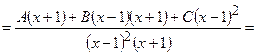

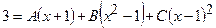 =
= 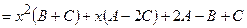
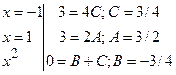
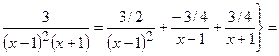
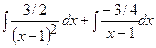 +
+

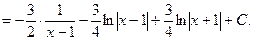
е) інтегрування тригонометричних функцій. Інтеграли виду 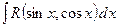 за допомогою універсальної підстановки
за допомогою універсальної підстановки  приводяться до інтегралів від раціональних дробів. В деяких випадках застосовують інші підстановки, які спрощують знаходження інтегралів. Розглянемо ці випадки.
приводяться до інтегралів від раціональних дробів. В деяких випадках застосовують інші підстановки, які спрощують знаходження інтегралів. Розглянемо ці випадки.
1) у випадку коли функція 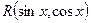 непарна відносно
непарна відносно 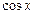 :
: 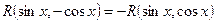 , робимо заміну
, робимо заміну 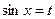 , а коли вона непарна відносно
, а коли вона непарна відносно 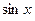 :
: 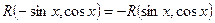 , то робимо заміну
, то робимо заміну 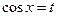 .
.
2) якщо функція  парна відносно
парна відносно 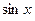 і
і 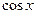 :
: 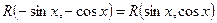 , то робимо заміну
, то робимо заміну

3) 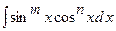 знаходиться підстановкою
знаходиться підстановкою 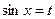 , якщо
, якщо  – ціле додатне непарне число, а
– ціле додатне непарне число, а 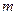 – ціле додатне парне число, або підстановкою
– ціле додатне парне число, або підстановкою 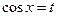 , якщо
, якщо 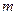 – ціле додатне непарне число, а
– ціле додатне непарне число, а  – ціле додатне парне число. У випадку, коли
– ціле додатне парне число. У випадку, коли  і
і 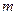 – цілі додатні парні числа, застосовують формули зниження степеня
– цілі додатні парні числа, застосовують формули зниження степеня 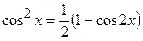 ,
, 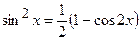 та
та 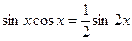 . Якщо
. Якщо  і
і 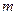 – цілі парні числа, але хоч одне з них від’ємне, або
– цілі парні числа, але хоч одне з них від’ємне, або  і
і 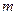 – цілі непарні і від’ємні числа, то застосовують підстановку
– цілі непарні і від’ємні числа, то застосовують підстановку 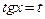 .
.
4) 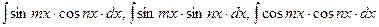 за допомогою формул:
за допомогою формул:
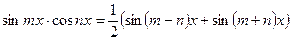 ;
;
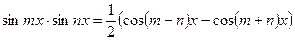 ;
;

зводяться до табличних.
Задача 6. Знайти інтеграли.
1) 

2) 
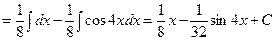
3) 
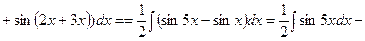
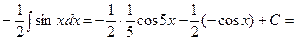

4) 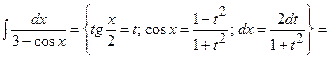
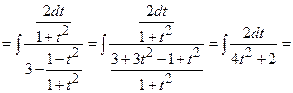
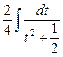 =
=

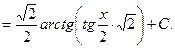
є) інтегрування ірраціональних виразів. Розглянемо деякі з них.
1) 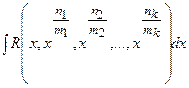 , де
, де  ,
, 
 – цілі додатні числа. Робимо заміну
– цілі додатні числа. Робимо заміну 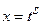 , де
, де 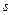 є спільним знаменником дробів
є спільним знаменником дробів 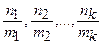 . Ця заміна приводить до інтегралу від раціональної функції аргументу
. Ця заміна приводить до інтегралу від раціональної функції аргументу  .
.
2)  , де
, де  ,
, 
 – цілі додатні числа,
– цілі додатні числа,  ,
, 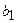 ,
, 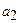 ,
, 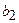 – дійсні числа. Заміна:
– дійсні числа. Заміна: 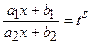 , де
, де 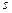 є спільним знаменником дробів
є спільним знаменником дробів  . Ця заміна приводить до інтегралу від раціональної функції аргументу
. Ця заміна приводить до інтегралу від раціональної функції аргументу  .
.
3) В інтегралах, що мають вирази : 3а)  , 3б)
, 3б) 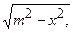
3в)  можна робити наступні заміни змінної:
можна робити наступні заміни змінної:
3а) 
3б) 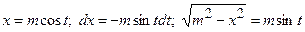
3в) 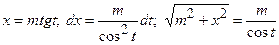
Задача 7. Знайти інтеграл.
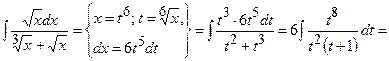
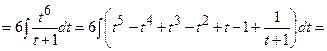
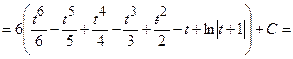
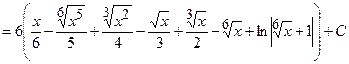
1.1.2 Визначений інтеграл.
Визначений інтеграл 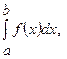 де функція
де функція 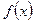 неперервна на відрізку інтегрування
неперервна на відрізку інтегрування  ,
, 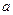 – нижня межа інтегрування,
– нижня межа інтегрування, 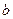 – верхня межа інтегрування, обчислюється за формулою Ньютона-Лейбніца:
– верхня межа інтегрування, обчислюється за формулою Ньютона-Лейбніца:
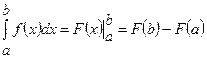 , де
, де  є первісною для підінтегральної функції
є первісною для підінтегральної функції 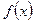 .
.
Властивості визначеного інтеграла
а) 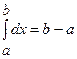
б) 
в) 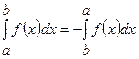
г)  ,
, 
д)  , де
, де  const
const
е) 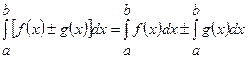
є) якщо відрізок інтегрування симетричний: 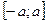 , то для парної підінтегральної функції
, то для парної підінтегральної функції 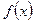
 , для непарної функції
, для непарної функції  .
.
Для знаходження первісної  при обчисленні визначеного інтеграла можна застосувати табличні інтеграли та методи інтегрування для обчислення невизначених інтегралів. Розглянемо деякі з них.
при обчисленні визначеного інтеграла можна застосувати табличні інтеграли та методи інтегрування для обчислення невизначених інтегралів. Розглянемо деякі з них.
а) заміна змінної під знаком визначеного інтеграла. Якщо функції  і
і  задовольняють умовам: функція
задовольняють умовам: функція 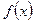 неперервна на
неперервна на  ; функція
; функція  має неперервну похідну
має неперервну похідну 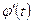 на
на 
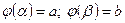 ; складена функція
; складена функція  визначена і неперервна на
визначена і неперервна на  , то
, то  .
.
б) формула інтегрування частинами у визначеному інтегралі
 .
.
Задача 8. Знайти інтеграли.
1) 
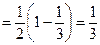 ;
;
2) 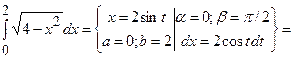
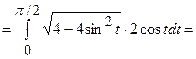


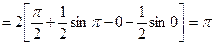 ;
;
3) 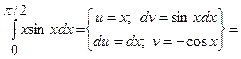


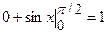
Читайте також:
- I. Аналіз контрольної роботи.
- I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
- I. ОСНОВНІ ЕТАПИ ВИКОНАННЯ КУРСОВОЇ РОБОТИ
- II. Вимоги безпеки перед початком роботи
- II. Вимоги безпеки праці перед початком роботи
- II. МЕТОДИЧНІ ВКАЗІВКИ
- II. СТРУКТУРА ТА ОБСЯГ КУРСОВОЇ РОБОТИ
- II.ТЕОРЕТИЧНІ ПИТАННЯ КУРСОВОЇ РОБОТИ
- III ОФОРМЛЕННЯ І ЗАХИСТ РОБОТИ
- III. Виконання бюджету
- III. Вимоги безпеки під час виконання роботи
- III. Вимоги безпеки під час виконання роботи
| <== попередня сторінка | | | наступна сторінка ==> |
| | | Невласні інтеграли першого та другого роду. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |