• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Методи перевірки гіпотез про закони розподілу випадкових величин

Статистичні гіпотези - це припущення, котрі відносяться до виду розподілу випадкової величини або окремих його параметрів. Оцінка відповідності статистичної гіпотези дослідним даним проводиться за допомогою статистичного критерію, який є стандартним прийомом оцінки відповідності висунутої гіпотези результатам спостереження. Задача випробування статистичних гіпотез виникає і тоді, коли обставини вимушують нас робити вибір між двома способами дії. Для визначення виду функції розподілу густини імовірності та оцінювання параметрів по емпіричним законам формулюється нульова гіпотеза (Н₀) про "відсутність розбіжностей". Нульова гіпотеза є прикладом статистичного висновку: якщо нульову гіпотезу відкинути, то висновок полягає в тому, що у сукупності, котра розглядається є розбіжності, тобто приймається альтернативна гіпотеза Н₁.

Приймемо, що випадкова величина 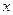підпорядкована закону розподілу з густиною імовірності 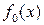-нульова гіпотеза.. У випадку, якщо виявиться , що гіпотеза непридатна, вважатимемо справедливою гіпотезу якій відповідає густина імовірності 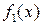. Задача формулюється наступним чином: знаючи конкретне значення величини 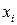випадкової величини 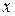визначити якій із гіпотез слід віддати перевагу. При вирішенні цієї задачі можливо припустити помилку двох видів: :

Н₀ відкидається, коли вона правильна - помилка 1-го роду.

Н₀ приймається, коли правильна Н_І - помилка ІІ- го роду.

Ймовірність з якою може бути відхилена нульова гіпотеза називається рівнем значущості. Рівень значущості задається заздалегідь. Ймовірність прийняття правильності рішення (гіпотеза Н₀ є вірною) називається довірчою ймовірністю.

Для перевірки істинності Н₀ гіпотези поступають наступним чином: Нехай функція 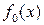має вид зображений на рис.

Якщо 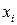знаходиться в інтервалі , то гіпотеза Н₀ із заданим рівнем значущості повинна бути визнана придатною. Якщо 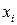знаходится лівіше 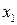або правіше 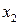, де ймовірність попадання випадкової величини близька до нуля, то тут можливі два випадки: або гіпотеза Н₀ невірна або відбулася вельми неправдоподібна в даному випадку подія. На практиці в цій ситуації вважають правдоподібним першу умову, тобто визнається помилковість нульової гіпотези Н₀ і вона відкидається. Для кількісної оцінки придатності гіпотези заштриховані області у хвостів функції називають критичними областями даної функції розподілу і вважають, що попадання випадкової величини в критичну область свідчить про неприйнятність аналізованої гіпотези.

Залежно від закону розподілу критична область може містити тільки ліву, тільки з праву або обидві заштриховані області у хвостах функції розподілу. Ймовірність попадання випадкової величини в критичну область характеризується рівнем значущості , який можна знайти із співвідношень:

; .

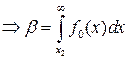Рис 11. Функція густини ймовірності випадкової величини 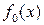. Кожна площа заштрихованої фігури чисельно рівна рівню значущості

В медицині вибір величини рівня значущості залежить від зіставлення втрат у разі помилкових висновків в ту або іншу сторону: чим вагоміші втрати від помилкового відхилення нульової гіпотези, тим меншою вибирається величина значення . Зазвичай, на практиці, значення приймається рівним 0,1; 0,05; 0,025; 0,01; 0,005; 0,001. Найчастіше використовується =0,05, яке означає, що при користуванні певним статистичним критерієм, в середньому в п'яти випадках із ста статистична гіпотеза, що перевіряється, буде відхилена помилково.

Читайте також:

1. B. Тип, структура, зміст уроку і методика його проведення.
2. Demo 11: Access Methods (методи доступу)
3. I. Доповнення до параграфу про точкову оцінку параметрів розподілу
4. I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
5. II. МЕТОДИЧНІ ВКАЗІВКИ
6. II. УЧЕБНЫЕ И МЕТОДИЧЕСКИЕ ПОСОБИЯ, ПРАКТИКУМЫ
7. IV. Закони ідеальних газів.
8. IV. КЕРІВНИЦТВО, КОНТРОЛЬ І НАДАННЯ ОРГАНІЗАЦІЙНО-МЕТОДИЧНОЇ ДОПОМОГИ ПРАКТИКАНТАМ.
9. IV. Учебно-методические рекомендации
10. IV. Электронное учебно-методическое обеспечение дисциплины.
11. V. ІНДИВІДУАЛЬНІ ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ ТА МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ДО ЇХ ВИКОНАННЯ
12. V. Обов'язки методиста кафедри педагогіки

Переглядів: 1499