• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Методичні вказівки

Використання вектора ознак. При застосуванні цього способу для об’єкта розпізнавання обчислюють його числові характеристики (ознаки). Вибираючи характеристик, одержуємо – вимірний вектор, який називається вектором ознак. Єдиного алгоритму обчислення ознак не існує і в кожному конкретному випадку слід вибирати свої характеристики. Основна вимога при цьому, щоб ознаки добре розрізняли об’єкти і були інваріантними до невеликих деформацій образів. Прикладами таких характеристик можуть бути: розміри об’єкта, яскравість його різних частин, кривизна контура, моментні характеристики, геометротопологічні ознаки тощо. Розпізнавання за вектором ознак є ефективним у випадку аналізу друкованих чи рукописних символів та подібних до них об’єктів. Робота ідентифікуючих систем при використанні вектора ознак складається з двох етапів: навчання системи і безпосередньо розпізнавання. Під час навчання налагоджуються внутрішні параметри системи – вектори еталонів , , де – кількість різних класів об’єктів, що розпізнаються. На цьому етапі системі подаються на вхід представники об’єктів різних класів і для кожного представника вказується, до якого класу він належить. Система обчислює вектор ознак для цього представника, а потім здійснює корекцію відповідного еталону за формулою: , де – параметр налагодження. Під час розпізнавання системі подається на вхід об’єкт для аналізу. Після обчислення його ознак система порівнює вектор 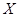з еталонами , . Клас об’єктів, еталон якого мінімізує , вважається розпізнаним.

Граматичні методи розпізнавання. Їх зручно використовувати для ідентифікації рукописних символів під час написання. Фріманом було запропоновано побудувати напрямки написання цифрами від 0 до 7:

1,1,1,0, 7,6,5,5, 4,4,4,4, 3,2,2,1

Після завершення написання символу одержуємо вектор кодів, належність якого до деякого класу еталонів зручно перевіряти відповідною граматикою. Зокрема, для символу ‘е’ ця граматика має вигляд

Розпізнавання ліній і кіл методом Хоуга. Розпізнавання ліній зводиться до знаходження відповідних пар параметрів рівняння прямої . Якщо зображення має розміри , то , . Розіб’ємо проміжок на рівних частин, – на рівних частин. Одержимо комірок можливих пар . Їм у методі Хоуга відповідає матриця розміру . На початку роботи алгоритму заповнюємо її нулями. Далі скануємо усі точки зображення. Якщо деяка точка є зафарбованою, збільшуємо на одиницю всі комірки матриці , які задовольняють умову . 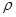Для цього перебираємо значень , а за ними знаходимо , ідентифікуючи всі такі комірки. Після сканування в тих комірках матриці , які відповідають реально існуючим на зображенні лініям, будуть знаходитись великі числа, а в усіх інших – малі. Описаний метод цілком підходить для ідентифікації кіл. Пошук у цьому випадку здійснюється у 3-вимірному просторі параметрів , які визначають координати центра і радіус кола.

Завдання для самостійної роботи

Задано зображення друкованого тексту. Розбити прямокутники, що описують кожний символ, на рівних клітин. Підрахувати для кожної клітини кількість пікселів символу, що попадають у неї. Отриманий –вимірний вектор використати як вектор ознак. Написати програми, які:

а) налагоджують систему розпізнавання на шрифт тексту:

1. m=5,n=5; 2. m=5,n=7; 3. m=7,n=7; 4. m=7,n=5;

б) розпізнають тексти, надруковані цим шрифтом:

5. m=5,n=5; 6. m=5,n=7; 7. m=7,n=7; 8. m=7,n=5.

Задано зображення окремо написаних символів. Розбити прямокутники, що описують кожний символ, на рівних клітин. Підрахувати відношення кількості пікселів символу, які попадають у кожну клітину, до їх загальної кількості. Одержаний –вимірний вектор використати як вектор ознак. Написати програми, які:

а) налагоджують системи розпізнавання на почерк користувача

9. m=5,n=5; 10. m=5,n=7; 11. m=7,n=7; 12. m=7,n=5;

б) розпізнають символи, написані цим користувачем

13. m=5,n=5; 14. m=5,n=7; 15. m=7,n=7; 16. m=7,n=5.

Написати програму, яка розпізнає в процесі написання символи:

17. ‘а’, ‘б’, ‘в’, ‘г’; 18. ‘д’, ‘е’, ‘з’, ‘и’; 19. ‘к’, ‘л’, ‘м’, ‘н’;

20. ‘п’, ‘р’, ‘с’, ‘т’; 21. ‘у’, ‘ф’, ‘х’, ‘ш’; 22. ‘ж’, ‘ю’, ‘я’, ‘ь’.

Граматики вказаних символів побудувати вручну. Процес написання символів зімітувати за допомогою миші.

Задано зображення креслення, яке містить різні геометричні фігури. Написати програми, які розпізнають:

23. Лінії. 24. Кола. 25. Трикутники. 26. Квадрати.

Читайте також:

1. I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
2. II. МЕТОДИЧНІ ВКАЗІВКИ
3. V. ІНДИВІДУАЛЬНІ ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ ТА МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ДО ЇХ ВИКОНАННЯ
4. VIІ. Короткі методичні вказівки до роботи студентів на практичному занятті
5. В ході аудиту фінансової звітності аудитором застосовуються методичні прийоми документального та фактичного контролю.
6. ВКАЗІВКИ ДО ВИКОНАННЯ КОНТРОЛЬНИХ РОБІТ
7. Вказівки до виконання контрольної роботи
8. ВКАЗІВКИ ДО ВИКОНАННЯ КОНТРОЛЬНОЇ РОБОТИ
9. Вказівки до виконання контрольної роботи
10. Вказівки до виконання контрольної роботи ( РГР ).
11. Вказівки до виконання контрольної роботи ( РГР ).
12. Вказівки до компоновки міжповерхового Перекриття

Переглядів: 377