• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Методичні вказівки

Код Хемінга. Припустимо, що необхідно виправити одиничну помилку у двійковому коді. Такий код складається з бітів, які переносять інформацію і контрольних бітів: всього бітів. Число повинно задовольняти умову . Співвідношення між , , для коду Хемінга наводяться у таблиці 5.1.

Таблиця 5.1

За цими параметрами визначають, які позиції сигналів будуть робочими, а які – контрольними. Практика показала, що номери контрольних бітів зручно вибирати як степені двійки, тобто 1,2,4,8,16,32... Потім обчислюють значення контрольних коефіцієнтів за правилом: сума одиниць на позиціях, які перевіряються, має бути парною. Позиції для перевірки вибирають так. Складають таблицю для ряду натуральних чисел у двійковому коді. Кількість її рядків . Першому рядку відповідає перевірочний коефіцієнт , другому - і так далі.

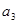0001 - 0010 - 0011 - 0100 -

0101 - 0110 - 0111 - 1000 -

1001 - 1010 - 1011 -

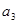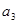У першу перевірку входять коефіцієнти, які містять одиницю у молодшому розряді ( , , , , ...), у другу – в другому розряді ( , , , , ...), у третю – в третьому розряді ( , , , ...) тощо.

Приклад 5.1. Побудувати код Хемінга для виправлення одиничної помилки при передачі комбінації 0101.

Розв’язання. Для нашого випадку . За таблицею 5.1 мінімальна кількість контрольних бітів , при цьому . Контрольні біти будуть знаходитись у позиціях 1,2,4; інформаційні – у позиціях 3,5,6,7: , , , . Для першої перевірки сума буде парною при . З другої перевірки випливає, що . Третя перевірка дасть . Остаточно одержуємо код 0100101.

Припустимо, що під час передачі виникла одинична помилка і було прийнято 0100111. Для знаходження позиції помилки виконуємо ті ж перевірки на парність, що й при кодуванні. Перша перевірка проходить, тому у молодший розряд позиції помилки записуємо 0. Друга і третя перевірки і не проходять, тому у відповідні біти позиції помилки записуємо 1. Звідси номер помилкової позиції .

Групові коди зручно задавати за допомогою породжуючих матриць, кількість рядків яких , а кількість стовпців - . Найчастіше така матриця має вигляд

,

де - інформаційна частина, 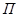- перевірочна частина. Алгоритм одержання перевірочних бітів за відомою інформаційною частиною коду може бути записаний так:

або

Для тестування наявності помилки у прийнятому сигналі обчислюється вектор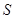

, .

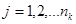Якщо він є нульовим, то помилки немає. Інакше будують допоміжну матрицю , де - одинична матриця порядку . Номер того стовпця матриці , який збігається з вектором 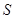, дає позицію помилково прийнятого біта.

Приклад 5.2. Побудувати груповий код за заданою твірною матрицею

для інформаційної комбінації 0101.

Розв’язання. В заданій інформаційній комбінації ненульовими є другий і четвертий біти. Тому для знаходження перевірочного коду додаємо за модулем 2 другий і четвертий рядки матриці П: . Отже 0101101 – коректуючий коду.

Припустимо, що замість нього була прийнята послідовність 0101001. Виконуємо перевірки:

Оскільки вектор 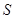не нульовий, то при передачі відбулася помилка. Будуємо матрицю

Звідси, оскільки вектор 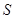співпадає з п’ятим стовпцем матриці , випливає, що помилково було прийнято саме п’ятий розряд.

Циклічні коди.В них інформаційна послідовність розглядається як масив коефіцієнтів многочлена, наприклад 1101 . Позначимо цей многочлен через . Як коректуючий код вибирається остача від ділення на наперед заданий породжуючий многочлен 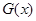. Тут — степінь 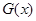, ділення многочленів виконується в арифметиці за модулем 2.

Приклад 5.3. Побудувати циклічний код, породжений многочленом для інформаційної послідовності 1001.

Розв’язання. Для нашого випадку . Домножуємо на і виконуємо ділення:

1001000ë1011

1011 1010

0000

1011

0000

Дописуємо коректуючий код 110 до інформаційної послідовності. Одержуємо 1001110.

Для перевірки правильності прийнятого коду він ділиться на 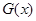. Якщо остача від ділення дорівнює нулеві, то помилки немає. Інакше підраховується кількість одиниць в остачі . Якщо , де 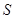– допустима кількість помилок, які виправляються даним кодом, то прийнята комбінація додається за модулем 2 до одержаної остачі: сума дасть виправлену комбінацію. Інакше циклічно зсовуємо отриману комбінацію вліво і ділимо її на породжуючий многочлен 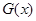. Виконуємо зсув і ділення доти, поки не задовольниться умова . Після цього додаємо за модулем 2 останню остачу до останнього діленого і здійснюємо циклічний зсув результату вправо на стільки розрядів, скільки було перед цим виконано зсувів вліво.

Приклад 5.4. Показати процес виправлення одиничної помилки в одержаному раніше коді 1001110.

Розв’язання. Нехай помилкова комбінація має вигляд 1000110. Виконуємо її ділення на породжуючий многочлен. Одержуємо остачу 011, для якої . Оскільки для нашого випадку , то потрібно виконати дії:

1. Циклічно зсуваємо 1000110 на один розряд вліво і ділимо ланцюг 0001101 на 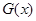. Одержуємо остачу 110, для якої .

2. 0001101 0011010, нова остача – 111.

3. 0011010 0110100, нова остача – 101.

4. 0110100 1101000, нова остача – 001. Оскільки тепер 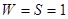, припиняємо зсуви вправо.

Додаємо за модулем 2 останню остачу (001) до останнього діленого (1101000) і виконуємо циклічний зсув результату (1101001) вправо на чотири розряди (тому що перед цим ми чотири рази зсовували прийняту комбінацію вліво). Одержана комбінація 1001110 вже не містить помилок.

Завдання для самостійної роботи

I. Побудувати код Хемінга і проілюструвати процес виправлення одиничної помилки при передачі ланцюжка. Варіанти:

1. 11000110110 2. 10010101100

3. 01101100011 4. 00110011100

5. 11011011011 6. 10111010101

7. 01101111000 8. 11110000011

II. Побудувати груповий код і проілюструвати процес виправлення одиничної помилки з використанням породжуючої матриці.

Варіанти:

9. 01110101011 10. 01100011100

11. 10001110110 12. 11101010101

13. 10101001010 14. 10101010101

15. 11010001011 16. 01001010110

17. 11010101101 18. 01010000111

19. 11001110101 20. 10110101101

III. Побудувати циклічний код і проілюструвати процес виправлення одиничної помилки з використанням породжуючого многочлена . Варіанти:

21. 10110110101 22. 00011110111

23. 11110001111 24. 01110101100

25. 11001100110 26. 10011001100

Читайте також:

1. I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
2. II. МЕТОДИЧНІ ВКАЗІВКИ
3. V. ІНДИВІДУАЛЬНІ ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ ТА МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ДО ЇХ ВИКОНАННЯ
4. VIІ. Короткі методичні вказівки до роботи студентів на практичному занятті
5. В ході аудиту фінансової звітності аудитором застосовуються методичні прийоми документального та фактичного контролю.
6. ВКАЗІВКИ ДО ВИКОНАННЯ КОНТРОЛЬНИХ РОБІТ
7. Вказівки до виконання контрольної роботи
8. ВКАЗІВКИ ДО ВИКОНАННЯ КОНТРОЛЬНОЇ РОБОТИ
9. Вказівки до виконання контрольної роботи
10. Вказівки до виконання контрольної роботи ( РГР ).
11. Вказівки до виконання контрольної роботи ( РГР ).
12. Вказівки до компоновки міжповерхового Перекриття

Переглядів: 504