Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Лекція 5 . Співідношення між різнимим формальними уточненнями АОФ. Теза Чорча.

План:

1.Теореми про співпадання різних класів алгоритмічно обчислювальних функцій.

2.Обґрунтування тези Чорча.

3.Значення і застосування тези Чорча.

Література:[3], [9], [10].

В різний час математиками були доведені теореми про співпадання класів функцій, які представляють різні формальні уточнення алгоритму та АОФ. Сформулюєме і доведемо деякі із них.

Теореми. Кожна ЧРФ є МНР-обчислювальною функцією.

Доведення.

1. Кожна базова функція є МНР- обчислювальною. Зокрема функція 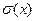обчислюється МНР програмою

1. Z(0).

Функція s(x) програмою

1. S(0).

Функція програмою

1. Т(m-1,0).

2. Нехай k-вимірна функція g та n-вимірні фукції g₁ … g_kобчислювальні відповідно МНР-програмами C, C₁,…, C_k. Тоді операція суперпозиції S^k(g,g₁,… ,g_k) обчислюється МНР програмою такого виду:

T(j,m+j+1) , j=0,…,n-1

G_j(m+1,…,m+n → m+n+j+1) , j=0,…,k-1

G (m+n+1,…,m+n +k → 0).

Тут m максимальне число команд у програмах C, C₁,…, C_k..

3) Нехай n–вимірна функція g та n+2 – вимірна функція h обчислюються відповідно МНР-програмами G та H. Тоді операція примітивної рекурсії R(g,h) обчислюється МНР програмою такого виду:

T(j,m+j+1) , j=0,…,n

G(m+1,…,m+n → m+n+3)

p) J(m+n+1,m+n+2,q)

p+1) H(m+1,…,m+n,m+n+2,m+n+3→m+n+3)

S(m+n+2)

J(1,1,p)

q) T(m+n+3, 0).

Тут m максимальне число команд в програмах G, H.

4) Нехай n+1–вимірна функція g обчислюється МНР-програмою G. Тоді операція мінімізації M(g) обчислюється МНР програмою такого виду:

T(j,m+j+1) , j=0,…,n

p) G(m+1,…,m+n+1 → 0)

J(0,m+n+2,q)

S(m+n+1)

J(1,1,p)

q)T(m+n+1, 0).

Тут m число команд в програмі G.

Отже, кожна ЧРФ є МНР-обчислювальною функцією.

Вірне і зворотне твердження: кожна МНР-обчислювальна функція є ЧРФ. Наведемо ідею доведення цього твердження. Нехай f(x₁,…,x_n) обчислюється МНР-програмою Р. Через R(x₁,…,x_n,t) позначимо функцію значенням якої є вміст 0–го регістру після t кроків роботи Р над x₁,…,x_n , або після q<t+1 кроків, якщо на q–ому кроці програма Р при роботі над x₁,…,x_n зупинилась. Через n(x₁,…,x_n,,t) позначимо функцію, значенням якої є номер команди після t кроків роботи Р над x₁,…,x_n , або 0, якщо програма Р при роботі над x₁,…,x_n зупинилась на кроці q<t+1.

Моделюючи роботу програму Р над x₁,…,x_n за t кроків, можна довести примітивну рекурсивність функцій R та n. Але f(x₁,…,x_n)=R(x₁,…,x_n, 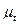(n(x₁,…,x_n,,t))=0), тому функція f - є ЧРФ.

Наслідок. Клас ЧРФ співпадає із класом МНР-обчислювальних функцій.

За кожною МТ можна збудувати еквівалентний їй НАМ, який задає те ж словникове відображення (домашнє завдання: спробувати довести це твердження ). З іншого боку, за кожним НА можна збудувати еквівалентну йому МТ. Отже, робимо висновок, клас МТ- обчислювальних функцій співпадає з класом НА-обчислювальних функцій.

В 1937 р. А. Тьюрінг встановив, що клас МТ-обчислювальних функцій співпадає з класом ЧРФ.

В різний час були доведені і інші твердження про перехресне співпадання різних класів функцій, що задають формальне уточнення алгоритму та АОФ.

Підсумовуючи всі ці результати можна сформулювати наступну узагальнюючу теорему:

Теорема. Наступні класи функцій співпадають:

1. Клас ЧРФ;

2. Клас програмованих на N функцій;

3. Клас МНР-обчислювальних функцій;

4. Клас функцій обчислювальних за Тьюрінгом;

5. Клас функцій обчислювальних за Марковим;

6. Клас функцій обчислювальних за Постом.

Враховуючи цей результат про співпадання класів функцій для шести різних формалізмів і те, що самі визначення цих формалізмів забезпечують ефективну обчислювальність заданих ними функцій, можна зробити припущення, що вони є різними математичним уточненнями інтуїтивного поняття алгоритмічно обчислювальної функції (АОФ). Вперше таке твердження стосовно рекурсивних функцій було висунуте в 1936 р. А. Чорчем і дістало назву ”теза Чорча”. В цьому ж році С. Кліні узагальнив тезу Чорча на випадок часткових функцій. В такому розширеному вигляді теза Чорча формулюється наступним чином:

Теза Чорча. Клас ЧРФ співпадає із класом часткових АОФ заданих на множині натуральних чисел.

Поняття АОФ не є строго визначеним математичним поняттям, тому теза Чорча строгому математичному доведенню не підлягає. Теза Чорча є природно-науковим фактом, який підтверджується такими результатами:

1. Істотно різні формальні уточнення АОФ, запропоновані різними авторами в різний час, виявились еквівалентними в розуміння задання ними одного і того ж класу функцій;

2. Перехід від задання функції в одному класі до задання цієї ж функції в іншому формалізмі є конструктивним, тобто він здійснюється за деяким алгоритмом (наприклад за операторним термом ефективно будується МНР-програма, яка задає ту ж функцію, що і цей терм);

3. Для кожного із таких формалізмів всі задані у ньому функції – алгоритмічно обчислювальні в інтуїтивному змісті;

4. Всі відомі до цих пір алгоритмічно обчислювальні функції виявились частково рекурсивними . Нікому ще не вдалося навести приклад функції, яка була би алгоритмічно обчислюваною і в той же час не була би ЧРФ.

Із тези Чорча, як наслідок, випливає, що клас РФ співпадає з класом тотальних (всюди визначених) АОФ, заданих на множині натуральних чисел.

Наукове значення тези Чорча полягає в наступному:

1. Прийняття тези Чорча перетворює інтуїтивні поняття алгоритму, обчислювальності, розв’язності в об’єкти математичного вивчення. Це дає можливість ставити і розв’язувати питання про алгоритмічну обчислювальність функцій , алгоритмічну розв’язність чи нерозв’язність масових проблем.

2. Використання тези Чорча, як своєрідної аксіоми, дозволяє у багатьох випадках замінити формальні задання алгоритмів на неформальні їх описи. Це, в ряді випадків, дає істотне спрощення доведень, дозволяє виділити основну ідею доведення чи побудови, звільняючи його від зайвих деталей. Проте такі доведення із використанням тези Чорча завжди вимагають ретельного обґрунтування. При виникненні сумнівів треба проводити формальні доведення.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Лекція 4. Нормальні алгоритми Маркова.	\|	І. ВСТУП

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.