Поняття про стійкість систем автоматичного регулювання

При виникненні збурення в САР вона відхилиться від заданої регульованої величини, а автоматичний регулятор буде наближатися повернути САР до заданого значення. У результаті такої взаємодії виникає перехідний процес.

Якщо з часом САР під впливом регулятора повернеться до заданого значення регульованої величини з тим або іншим ступенем точності, то перехідний процес називається таким що сходиться, а САР — стійкою. Якщо ж з часом САР під впливом регулятора не повертається до заданого значення регульованої величини, а усе більше буде відхилятися від нього, такий перехідний процес називається розбіжний, а САР — не стійкою.

Щоб САР виконувала своє призначення, вона повинна бути насамперед стійкою. Тому аналіз САР на стійкість є однією з головних задач теорії автоматичного регулювання.

Характер поведінки САР у перехідному процесі залежить від характеристичного рівняння САР і визначається видом його коренів. Можливі наступні види коренів характеристичного рівняння.

1. Усі корені характеристичного рівняння — натуральні і нерівні. Загальний вид рішення рівняння може бути в цьому випадку записаний:

, (4.1)

де A₁, А₂, ..., А_n – постійні інтегрування; р₁, р₂, ..., р_n – корені характеристичного рівняння.

Якщо всі корені характеристичного рівняння будуть від’ємними, то кожне з рівняння, що складають рівняння (4.1) буде загасаючою експонентою, весь перехідний процес з часом (t => ∞) аперіодично буде наближатися до нуля і САР буде стійкою (рис. 4.1, криві 1).

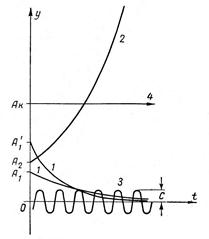1 – корені натуральні, різні, від’ємні; 2 – корінь натуральний, додатній; 3 – пари уявно спряжених коренів; 4 – нульовий корінь.

Рисунок 4.1 – Перехідний процес САР при різних видах коренів характеристичного рівняння.

Якщо серед коренів характеристичного рівняння буде хоча б один додатній корінь, то в рішенні рівняння (4.1) з'явиться доданок, що представляє необмежено зростаючу експоненту. Після закінчення досить тривалого проміжку часу всі інші доданки перетворяться в нуль, а цей доданок буде необмежено зростати, перехідний процес буде аперіодично розбіжним, а САР – нестійкою (рис. 4.1, крива 2).

2. Характеристичне рівняння має один нульовий корінь, а інші корені натуральні, різні і від’ємні. У цьому випадку нульовий корінь дасть постійну складову A_k, а все рівняння буде мати вигляд:

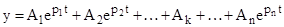. (4.2)

Після закінчення досить тривалого проміжку часу всі складові експоненти будуть наближатися до нуля, а y буде наближатися до постійної величини A_k (рис. 4.1, пряма 4) і САР буде знаходитися на межі стійкості.

3. Характеристичне рівняння має одну пару уявних спряжених коренів, а інші корені натуральні, різні і від’ємні. У цьому випадку уявні корені дадуть у загальному рішенні складову С sin(ωt + φ)

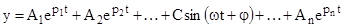. (4.3)

Після закінчення досить тривалого проміжку часу всі складові експоненти будуть наближатися до нуля, а складова від уявних коренів дасть незатухаючі синусоїдальні коливання (рис. 4.1, крива 3) і САР буде не стійкою.

4. Характеристичне рівняння має одну пару спряжених комплексних коренів, а інші корені натуральні, різні і від’ємні. У цьому випадку комплексні корені дадуть у загальному рішенні складову С sin(ωt + φ)

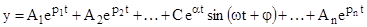, (4.4)

Складова комплексних коренів представляє собою синусоїду з перемінною амплітудою C .

Якщо дійсна частина комплексних коренів α буде від’ємна, то виниклі коливання будуть загасаючими, а САР – стійкою.

Якщо ж величина α буде додатна, то коливання будуть незатухаючими, а САР – не стійкою. Ці випадки показані на мал. 4.2.

5. Характеристичне рівняння має s кратних коренів, а інші корені натуральні, різні і від’ємні.

Находимо загальне рішення рівняння для цього випадку

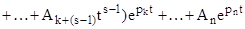. (4.5)

Тільки в тому випадку, якщо кратні корені будуть від’ємними, по закінченні досить тривалого проміжку часу перехідний процес стане загасаючий, а САР буде стійкою. З приведеного аналізу можна зробити наступний висновок.

Перехідний процес буде загасаючий, а система автоматичного регулювання – стійкою, якщо характеристичне рівняння буде мати корені тільки з від’ємними натуральними частинами.

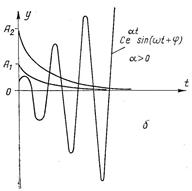а – при від’ємній натуральній частині кореня (α < 0); б – додатні натуральній частині кореня (α > 0).

Рисунок 4.2 – Перехідний процес САР при наявності комплексних коренів характеристичного рівняння.

Цей висновок справедливий тільки для лінійних систем. У дійсності ж у більшості випадків системи автоматичного регулювання нелінійні. Однак при несуттєвій нелінійності при малих відхиленнях регульованої величини нелінійну систему можна замінити її лінійною моделлю і по ній вирішувати питання про стійкість реальної системи («стійкість у малому»). Для цього рівняння системи розкладають у ряд Тейлора і відкидають з нього всі члени вище першого порядку. Таке спрощене рівняння називається лінеаризованим. Виникає питання, наскільки висновок про стійкість системи, зроблений по лінеаризованих рівняннях, буде справедливий для реальних систем. На це питання виняткової важливості для практики була дана відповідь росіянином вченим А. М. Ляпуновим (1892 р.) у теоремах про стійкість, що ми приводимо без доказу.

Теорема 1. Якщо характеристичне рівняння лінеаризованої системи, має всі корені з від’ємними натуральними частинами, то дійсна система буде стійка. При цьому ніякі, відкинуті при лінеаризації рівняння, члени другого і вищого ступенів відхилення регульованого параметра не можуть змінити стійкість системи.

Теорема 2. Якщо характеристичне рівняння лінеаризованої системи має хоча б один корінь з додатною натуральною частиною, то дійсна система буде нестійка. При цьому ніякі, відкинуті при лінеаризації, члени другого і вищого ступенів відхилення регульованого параметра не можуть додати системі стійкість.

Як видно з усього викладеного, для аналізу САР на стійкість необхідно знати корені їхніх характеристичних рівнянь, тобто вирішувати їх, що викликає ряд труднощів, починаючи з рівнянь вище третього ступеня.

Тому багато вчених шукали різні непрямі ознаки і правила, що дозволили б без рішення диференціальних і їхніх характеристичних рівнянь визначати стійкість САР.

Такі правила звичайно називають критеріями стійкості.

З усіх критеріїв найбільш розповсюдженим є критерії стійкості Гурвіца і Найквіста – Михайлова, які ми розглянемо без доказів.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Практичне заняття №4	\|	Критерій стійкості Гурвіца

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.