
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Параметри
Загальні відомості, класифікація, геометричні та кінематичні
ГЛАВА 4. ЦИЛІНДРИЧНІ ТА КОНІЧНІ ЗУБЧАСТІ ПЕРЕДАЧІ
ЧЕРВ’ЯЧНІ ПЕРЕДАЧІ. РЕДУКТОРИ
РОЗДІЛ 2. ЗУБЧАСТІ ПЕРЕДАЧІ.
Основи вибору механічних передач
Проектуючи привод, виникає необхідність вибору виду передач. Цей вибір залежить від конкретних умов роботи привода і вимог, які ставляться до нього.
Загальні вимоги до передач: надійність та необхідна довговічність передачі; простота конструкції; компактність і малі ґабаритні розміри; незначний опір руху, особливо в момент пуску двигуна; порівняно висока точність перетворення руху (кінематична точність); безшумність роботи та вібростійкість; простота керування, в тому числі автоматичного і дистанційного. Технологічні вимоги, які ставляться перед машиною: сталість передатного відношення; безступінчасте реґулювання швидкості; високий ККД; маса; точність виготовлення передачі; вартість /наприклад, черв'ячні передачі при інших рівних умовах дорожчі за прості зубчасті/. Щодо ґабаритних розмірів, то це також важливий критерій і ним не можна нехтувати.
Вимоги, які ставляться до проектованого привода, можуть реалізовуватися з використанням різним варіантів передач та їхніх кінематичних схем. Проектуючи привод, необхідно пам'ятати, що першочерговою задачею є вибір оптимальних передач на основі оцінки їх за критеріями порівняння.
Найпоширенішими у сучасному машинобудуванні та приладо-будуванні серед механічних передач є зубчасті передачі.
Застосовують зубчасті передачі в широких діапазонах швидкостей (до 150 м/с), потужностей (до 100 тисяч кіловат) і передатних чисел.
Переваги зубчастих передач порівняно з іншими видами передач: сталість передатного числа; висока навантажувальна здатність; високий ККД (0,96¸0,98 для однієї пари коліс); малі габаритні розміри у порівнянні з іншими видами передач за рівних умов; велика надійність в роботі, простота обслуговування; порівняно невеликі навантаги на вали та опори.
Недоліки зубчастих передач: неможливість безступінчастої зміни передатного числа; високі вимоги до точності виготовлення і монтажу; шум при великих швидкостях; погані амортизувальні властивості (що негативно впливає на компенсацію динамічних навантаг); громіздкість при великих відстанях між вісями ведучого і веденого валів; потреба у спеціальному обладнанні та інструменті для нарізання зубців; зубчаста передача не уберігає машину від можливих небезпечних перевантажень.
Класифікують зубчасті передачі та колесаза такими ознаками (рис. 4.1): а) за взаємним розміщенням вісей коліс – з паралельними (циліндричні, див. рис. 4.1, а-г), з вісями, що перетинаються (конічні, див. рис. 4.1, е-ж), з мимобіжними вісями (ґвинтові, див. рис. 4.1. д, з); б) за розміщенням зубців відносно твірних коліс – прямозубі, косозубі, шевронні та з криволінійним зубцем; в) за конструктивним оформленням – відкриті і закриті; г) за коловою швидкістю – дуже тихохідні (до 0,5 м/с), тихохідні (0,5¸3 м/с), середньотихохідні (3¸15 м/с), швидкохідні (більше 15 м/с); ґ) за кількістю ступенів – одно- і багатоступінчасті; д) за розміщенням зубців у передачі та колесах – зовнішнє, внутрішнє (див. рис. 4.1, г) і рейкове зачеплення (див. рис. 4.1, ґ); е) за формою профілю зубця – з евольвентними і з неевольвентними зубцями; з) за точністю зачеплення.
Геометричні та кінематичні параметри.Зауважимо перш за все, що усі поняття і терміни, які стосуються геометрії та кінематики зубчастих передач (рис. 4.2), стандартизовані. Стандарти встановлюють терміни, визначення і позначення, а також методи розрахунку геометричних параметрів.
Параметрам шестірні приписують індекс 1, а колеса – 2 (рис. 4.2). Крім того, розрізняють індекси, що відносяться: w – до початкового обводу або кола; b – до основного обводу або кола; а – до обводу або кола вершин і головок зубців; f – до обводу або кола западин та ніжок зубців.
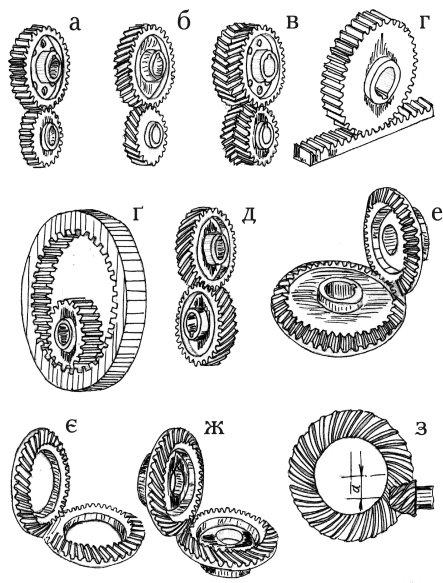
Рис. 4.1. Зубчасті передачі
Цим концентричним обводам або колам відповідають діаметри: початковий dw, основний db, вершин зубців dа, западин df, ділильний d. Якщо шестірня, то dw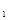 , db
, db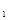 , dа
, dа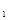 ,df
,df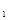 , d1, а колеса – відповідно dw
, d1, а колеса – відповідно dw , db
, db ,dа
,dа , df
, df , d2.
, d2.

Рис. 4.2. Параметри зубчастої передачі
Основним параметром зубчастого зачеплення є модуль зубців m – величина, пропорційна кроку Р по ділильному обводу, тобто циліндрові, на якому крок зубчастого колеса дорівнює кроку вихідного контуру – кроку створювальної рейки. Отже, m=Р/p.
Крок Р, як і довжина обводу або кола, є кратним числу p і тому незручним для прийняття його як основного параметра зачеплення.
Для косозубих передач розглядають колові та нормальні кроки і відповідно модулі.
Коловий ділильний крок Рt – це відстань між однойменними профілями сусідніх зубців, виміряна по дузі ділильного обводу або кола зубчастого колеса. Зрозуміло, що pd=zРt звідки Рt=pd/z. Відповідно коловий модуль mt=d/z.
Нормальний крок Рn – найкоротша відстань по ділильному обводу як циліндру між однойменними профільними поверхнями двох суміжних зубців Рn=Рtcosβ (тут β – кут нахилу лінії зубців по ділильному обводу). Відповідно нормальний модуль mn=m=mtcosβ. Для прямозубих передач колові та нормальні кроки і модулі відповідно співпадають.
Модулі стандартизовані в діапазоні 0,05¸100 мм. Стосовно середнього машинобудування найуживаніші модулі від 1 до 45 мм. (перевага надається 1-му рядові):
1-ий ряд: 1; 1,25; 1,5; 2; 2,5; З; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32; 40;
2-ий ряд: 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14;
18; 22; 28; 36; 45.
Для редукторів допускають також модулі 1,6; 3,15; 6,3; 12,5 мм.
Для косозубих циліндричних коліс стандартними назначають нормальні модулі. Параметри початкового контуру циліндричних зубчастих коліс стандартизовані (ГОСТ 13755); кут профілю µ=200. Висота головки зубця hα=h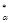 m, h
m, h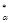 =1, висота ніжки зубців hf=h
=1, висота ніжки зубців hf=h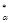 m=(h
m=(h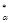 +c*)m. Глибина заходу зубців h3=2m; радіальний проміжок між зубцями c=0,25m (якщо нарізують довбачами – до 0,35m); радіус викруглення біля кореня зубця ρf=0,38m.
+c*)m. Глибина заходу зубців h3=2m; радіальний проміжок між зубцями c=0,25m (якщо нарізують довбачами – до 0,35m); радіус викруглення біля кореня зубця ρf=0,38m.
Кінематичні характеристики зубчастого зачеплення. Із курсу “Теорія машин і механізмів” основна теорема зачеплення свідчить: профілі зубців двох спряжених коліс мають бути такими, щоб спільна нормаль до них у будь-якій точці дотику профілів проходила через полюс зачеплення Р, який ділить міжвісеву відстань О1О2 на відрізки, що обернено пропорційні кутовим швидкостям коліс. Саме евольвентне зачеплення відповідає вимогам основної теореми зачеплення, оскільки точка Р займає постійне положення на лінії центрів О1О2 (рис. 4.2), звідки
ω1/ω2=(РО2)/(РО1)=dw2/dw1=u, (4.1)
де dw2 та dw1 – діаметри початкових обводів веденого і ведучого коліс.
Рівність колових швидкостей 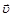 1=
1=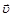 2 або ω1dw1=ω2dw2 показує, що при обертанні зубчастих коліс обводи діаметрами dw1 та dw2 перекочуються одне по одному без ковзання.
2 або ω1dw1=ω2dw2 показує, що при обертанні зубчастих коліс обводи діаметрами dw1 та dw2 перекочуються одне по одному без ковзання.
Лінія перетину бічної поверхні зубця з ділильною, початковою, основною та іншими співвісними поверхнями зубчастого колеса називається лінією зубця.
Передатне число зубчастої передачі u=z2/z1, де z2 – кількість зубців колеса, а z1 – кількість зубців шестірні; z2≥z1, а тому відповідно u≥1.
Центральний кут концентричного обводу зубчастого колеса, що дорівнює 2p/z (z – кількість зубців колеса), називається кутовим кроком зубціві позначається t (t=2p/z).
Кут нахилу лінії зубця (кут нахилу зубця) – гострий кут між лінією зубця та лінією перетину співвісної поверхні, якій належить ця лінія зубця, з площиною, що проходить через вісь зубчастого колеса. Позначається кут нахилу зубця β. Кут нахилу на ділильному циліндрі приймають: для косозубих коліс β=8¸220 (рідко до 250), у роздвоєних ступенях редукторів для кращого самоустановлення β≥300; для шевронних зубців β=25¸400.
Кут повороту зубчастого колеса передачі від положення входу зубця в зачеплення до виходу його із зачеплення називається кутом перекриття jγ. Відношення кута перекриття зубчастого колеса передачі до його кутового кроку називається коефіцієнтом перекриття: εµ=jγ/t.
Для циліндричних косозубих, шевронних та інших передач коефіцієнт перекриття εγ складається із коефіцієнтів перекриття торцевого εµ і вісевого εβ. Кут повороту зубчастого колеса циліндричної передачі від положення входу в зачеплення торцевого профілю зуба до виходу із зачеплення називається кутом торцевого перекриття jµ.
Коефіцієнтом торцевогоперекриття εµ називається відношення кута торцевого перекриття зубчастого колеса циліндричної передачі jµ до кутового кроку t.
Коефіцієнтом вісевого перекриття εβ називається відношення кута вісевого перекриття зубчастого колеса косозубої циліндричної передачі jβ до кутового кроку t.
Коефіцієнт перекриття для косозубих та інших передач
εγ=εµ+εβ. (4.2)
Коефіцієнт торцевого перекриття для передач без зміщення може визначатися залежністю
εµ=1,88-3,2(1/z1±1/z2), (4.3)
де знак "+" для зовнішнього і "–" для внутрішнього зачеплення. Для передач зі зміщенням εµ визначають за ГОCТ 16532.
Читайте також:
- Аналітичні параметри
- Аналітичні параметри
- Артеріальний пульс, основні параметри
- Будова, характеристики і параметри біполярного транзистора
- Варіатори та їхні основні параметри
- Види передавальних пристроїв РЛС РТВ та їх параметри
- Вікна та їх основні параметри
- Вплив методів перепроектування робіт на базові параметри роботи
- ВТОРИННI ПАРАМЕТРИ ДОВГОЇ ЛIНIЇ
- Втрата непараметричними критеріями згоди „свободи від розподілу” при складних гіпотезах
- Геометричні, кінематичні, силові та динамічні параметри
- Головні параметри кар’єрних полів
| <== попередня сторінка | | | наступна сторінка ==> |
| Основні кінематичні та силові співвідношення | | | Розрахунки на міцність |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |