• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розв’язання лінійних систем методом Гауса

Універсальним методом розв’язання систем лінійних алгебраїчних рівнянь є метод Гауса, який полягає в послідовному виключенні змінних.

Нехай дана система т лінійних рівнянь з п невідомими

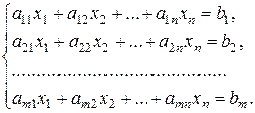(4.6)

Процес розв’язання за методом Гауса складається з двох етапів. На першому етапі (прямий хід) система зводиться до ступінчастого (зокрема, до трикутного) вигляду.

Наведена нижче система має ступеневий вигляд:

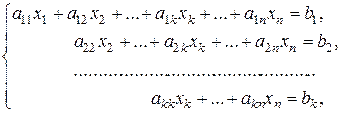
де .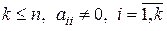

На другому етапі (обернений хід ) йде послідовне знаходження невідомих з цієї ступінчастої системи.

Опишемо метод Гауса детальніше.

Прямий хід.

Вважатимемо, що елемент 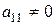(якщо 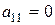, то першим в системі запишемо рівняння, в якому коефіцієнт при 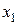відмінний від нуля ).

Перетворимо систему (4.6), виключивши невідому 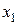з усіх рівнянь, крім першого, використовуючи елементарні перетворення системи. Для цього помножимо обидві частини першого рівняння на 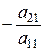і додамо почленно до другого рівняння системи. Потім помножимо обидві частини першого рівняння на 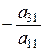і додамо до третього рівняння системи. Продовжуючи цей процес, отримаємо еквівалентну систему

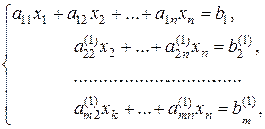
де 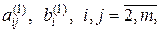– нові значення коефіцієнтів і вільних членів, які отримуються після першого кроку.

Аналогічно, вважаючи 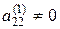, виключаємо невідому 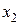з усіх рівнянь системи, крім першого і другого, і так далі. Продовжуємо цей процес поки це можливо.

Якщо в процесі приведення системи (4.6) до ступінчастого вигляду з’являться нульові рівняння, тобто рівняння вигляду 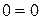, то їх відкидаємо. Якщо ж з’являться рівняння вигляду 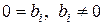, то система несумісна.

Обернений хід.

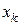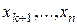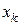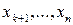Розв’язуємо ступінчасту систему, яка, взагалі, має безліч розв’язків. В останньому рівнянні цієї системи виражаємо першу невідому через інші невідомі . Потім підставляємо значення в передостаннє рівняння системи і виражаємо невідому через невідомі ; потім знаходимо 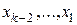. Надаючи вільним невідомим 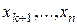довільних значень, отримаємо безліч розв’язків системи.

Зауваження.

1. Якщо ступінчаста система виявиться трикутною, тобто 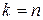, то початкова система має єдиний розв’язок. З останнього рівняння знаходимо 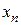, з передостаннього рівняння 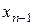, далі, піднімаючись по системі вверх, знаходимо всі інші невідомі .

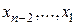2. На практиці зручно замість перетворень системи виконувати елементарні перетворення над рядками розширеної матриці системи, тобто приводити її до трапецієвидного вигляду. Зручно, щоб коефіцієнт 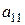дорівнював 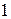або 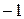(переставляємо рядки або множимо рядок на ).

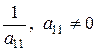Теоретичні питання

4.1. Яка система називається лінійною?

4.2. Що називається основною матрицею і розширеною матрицею системи т лінійних рівнянь з п невідомими?

4.3. Що називається розв’язком системи т лінійних рівнянь з п невідомими?

4.4. Яка система лінійних рівнянь називається сумісною і яка – несумісною?

4.5. Яка система лінійних рівнянь називається визначеною і яка – невизначеною?

4.6. Які системи називаютьсяеквівалентними?

4.7. Яка система лінійних рівнянь називається однорідною?

4.8. Які перетворення системи називають елементарними?

4.9. Яка система лінійних рівнянь називається невиродженою і яка – виродженою?

4.10. Скільки розв’язків має невироджена система?

4.11. Запишіть в матричному вигляді розв’язок невиродженої системи .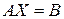

4.12. Запишіть формули Крамера.

4.13. Сформулюйте теорему Кронекера-Капеллі.

4.14. В якому випадку система лінійних рівнянь має єдиний розв’язок?

4.15. В якому випадку система лінійних рівнянь має безліч розв’язків?

4.16. Яке правило розв’язання довільних лінійних систем?

4.17. В чому полягає метод Гауса?

Задачі та вправи

В задачах 4.1–4.2 розв’язати системи: а) матричним способом; б) за формулами Крамера.

4.1.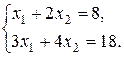

4.2.

4.3. Розв’язати систему:

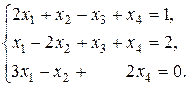
Розв’язок. Знаходимо ранги основної та розширеної матриць системи:

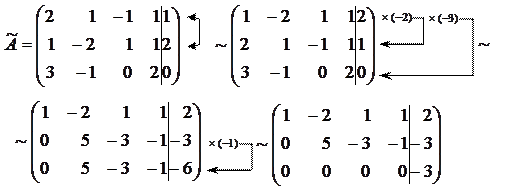
Отримали 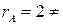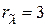. Так як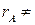 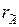, то система несумісна. t

4.4. Розв’язати систему:

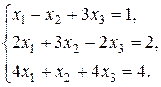
Розв’язок. Знаходимо ранги основної та розширеної матриць системи:

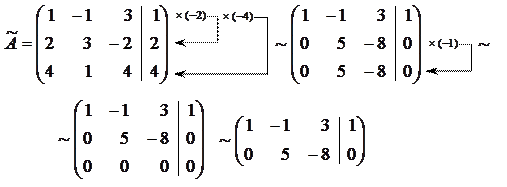
Отримали 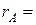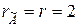. Отже, система сумісна.

Кількість невідомих – .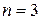

Так як 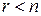, то система має безліч розв’язків.

В якості базисного мінора можна взяти, наприклад, мінор

.

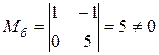Тоді базисними будуть невідомі 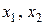, а 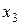– вільна.

Дана система еквівалентна системі:

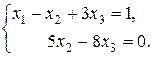
або

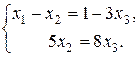
За методом Гауса знаходимо

Покладемо 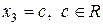, тоді множина розв’язків системи має вигляд

.

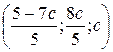Перевірка:

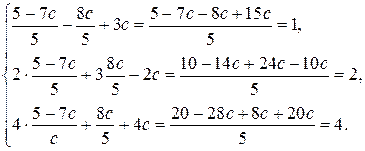
Відповідь: 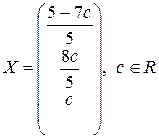. t

4.5. Розв’язати систему:

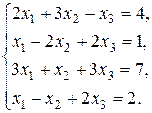
Розв’язок. Знаходимо ранги основної та розширеної матриць системи:

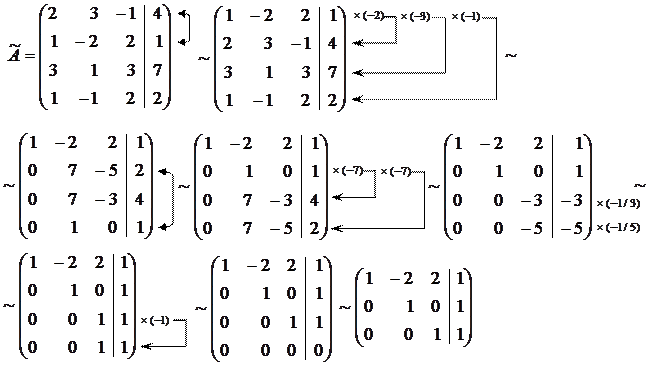
Отримали 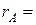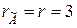. Отже, система сумісна.

Кількість невідомих – .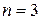

Так як 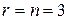, то система має єдиний розв’язок.

Дана система еквівалентна системі:

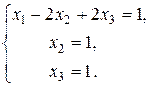
За методом Гауса знаходимо

.

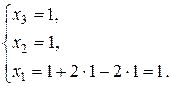Перевірка:

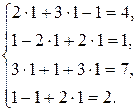
Відповідь: 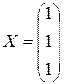. t

4.6. Розв’язати систему методом Гауса:

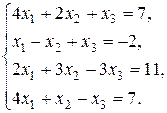
Розв’язок.

Прямий хід. За допомогою елементарних перетворень зведемо розширену матрицю системи до трапецієвидного вигляду:

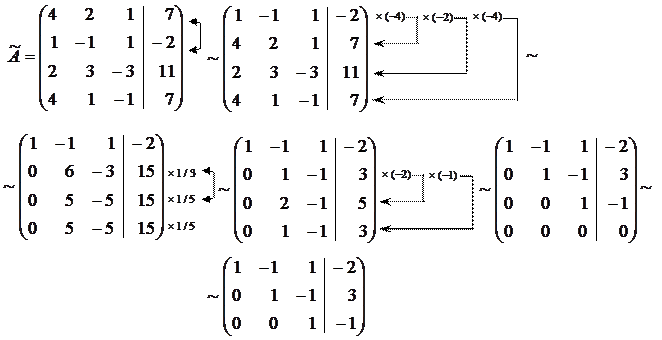
Цій матриці відповідає система:

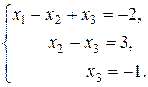
Обернений хід. Знаходимо

.

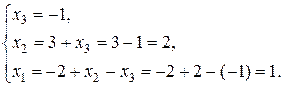Перевірка:

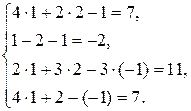
Відповідь: 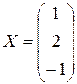. t

Читайте також:

1. Active-HDL як сучасна система автоматизованого проектування ВІС.
2. I. Органи і системи, що забезпечують функцію виділення
3. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
4. II. Анатомічний склад лімфатичної системи
5. II. Бреттон-Вудська система (створена в 1944 р.)
6. II. Критерій найбільших лінійних деформацій
7. III етап. Системний підхід
8. IV. Перевірка розв’язання і відповідь
9. IV. Розподіл нервової системи
10. IV. Система зв’язків всередині центральної нервової системи
11. IV. УЗАГАЛЬНЕННЯ І СИСТЕМАТИЗАЦІЯ ВИВЧЕНОГО
12. IV. Філогенез кровоносної системи

Переглядів: 1309