• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Основні поняття та означення.

Тема 3. Матриці. Операції над матрицями.

Означення. Матриця у загальному випадку – форма задання відношень, яка представляє собою прямокутну таблицю, що складається з рядків та стовпців, при цьому елементом матриці може бути будь-який об’єкт.

Будь-яку систему відношень можна подати у вигляді матриці.

Матриці позначають великими літерами А, В, С, ... та круглими або квадратними дужками.

Матриця, яка містить m рядків та n стовпців, називається матрицею m ´ n. Отже в загальному випадку матрицею розміру m ´ n можна подати у вигляді:

.

Можна подати матрицю у скороченому вигляді

А = [ а_іj ]_mxn , (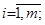

А – це є прямокутна матриця, яка має m-рядків, n-стовпців. Загальний елемент a_ij - це елемент, який лежить на перетині і-го рядка та j-го стовпця.

Числа, що складають матрицю, називаються її елементами. При двохіндексному позначені елементів матриці перший індекс вказує на номер рядка, а другий індекс - номер стовпця, на перетині яких міститься даний елемент.

a_іj – елемент матриці

a_(і) – і-й порядок a_і={a_і1, a_і2...., a_іj, a_іn}

a_(j) – j-й стовпець a_j={a_1j, a_2j, a_ij…, a_mj}

Наведемо деякі приклади.

у₁ у₂ у₃ у₄

А = 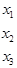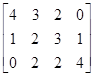- числова матриця.

Матриця А є прямокутна, має розмір 3 ´ 4, причому а₁₁= 4, а₁₂= 3,

а₁₃ = 2, а₁₄ = 0, а₂₁ = 1, а₂₂ = 2, а₂₃ = 3, а₂₄ = 1, а₃₁ = 0, а₃₂ = 2, а₃₃ = 2, а₃₄ = 4.

Нехай

х – множина країн розвинутих тобто (інвестори)

у – множина країн мало розвинутих .

Числа – це будь-яка допомога, виражена в якихось одиницях (країни інвестори ® донори країни ).

Приклад матриці відношення порядку

x₁ x₂ x₃

елементи такої матриці є:

x₁ =x₁, x₁ > x₂, x₁ < x₃, x₂ < x₁, x₂ = x₂, x₂ = x₃, x₃ > x₁, x₃ = x₂, x₃ = x₃.

Типи матриць. Матриця може мати будь-яку кількість рядків і стовпців

(тобто скінчену та нескінчену). Будемо розглядати скінчені матриці.

Означення. Якщо матриця складається з одного рядка, то вона називається матрицею - рядком, або вектором-рядком. Її розміри (1´ n). Матриця , що складається з одного стовпця, називається матрицею-стовпцем або вектором-стовпцем. Її розміри (m´n).

Х = [x₁, x₂, x₃,..., x_m], (j = ; i = 1 ) - матриця рядок;

Y = j = 1) - матриця стовпець.

Матриця називаєтьсянульовою, якщо її елементи дорівнюють нулю. Нульові матриці можуть мати різні розмірності. (квадратна, прямокутна). Дві матриці називаються рівними, якщо вони мають однаковий розмір і в них рівні між собою розміщені елементи.

Означення. Матриця називається квадратною, коли число її рядків дорівнює числу її стовпців. Якщо квадратна матриця має n стовпців, то говорять, що матриця має порядок n. (m = n). Вона позначається :

А=[a_ij]_nхn.

Розглянемо квадратну матрицю порядку n

.

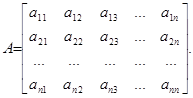Її елементи, що мають однакові індекси рядків і стовпців, утворюють так звану головну діагональ: а₁₁, a₂₂, a₃₃, ..., a_nn.

Означення. Квадратна матриця називається діагональною, якщо всі її елементи, розміщені поза головною діагоналлю, дорівнюють нулю.

D = diag [d_ij ]_n´n = diag [d_ij ]_n

1. D = [d_ij ]_4´4 =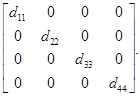

Означення. Якщо в діагональній матриці всі елементи дорівнюють 1, то таку матрицю називають одиничною матрицею n-го порядку. Позначають одиничну матрицю Е_n.

Одинична матриця завжди квадратна.

Е =

Квадратна матриця називається симетричною, якщо для усіх i та j мають місце рівності a_ij = a_ji.

Розглянемо приклади:

B =

Матриця В є діагональною 4-го порядку; L - скалярна 3-го порядку; М - симетрична матриця 3-го порядку; О - нуль-матриця розміру (3´3).

Квадратна матриця називається верхньо - (нижньо) – трикутною, якщо дорівнюють 0 нулю всі елементи під (над) головною діагоналлю.

A = - верхньотрикутна матриця n-того порядку,

B_n´n = 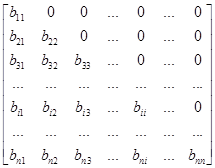- нажньотрикутна матриця n - го порядку.

Діагональна матриця є частинним випадком як верхньої (А), так і нижньої (В) трикутних матриць.

Рівність матриць. Дві матриці А = [ a_ij ] та B = [ b_ij ] називаються рівними (А=В), якщо вони мають однакові розміри, тобто однакове число рядків та стовпців, та їхні відповідні елементи рівні між собою: a_ij = b_ij .

Читайте також:

1. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
2. II. Поняття соціального процесу.
3. V. Поняття та ознаки (характеристики) злочинності
4. А/. Поняття про судовий процес.
5. Адвокатура в Україні: основні завдання і функції
6. Адміністративний проступок: поняття, ознаки, види.
7. Адміністративні провадження: поняття, класифікація, стадії
8. Акти застосування юридичних норм: поняття, ознаки, види.
9. Амортизація основних засобів, основні методи амортизації
10. Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
11. Артеріальний пульс, основні параметри
12. АРХІВНЕ ОПИСУВАННЯ: ПОНЯТТЯ, ВИДИ, ПРИНЦИПИ І МЕТОДИ

Переглядів: 1690