Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Короткі теоретичні відомості

Позацентрове розтягання (стискання) прямого бруса

Позацентрове розтягання-стискання (eccentric tension-compression) є окремим випадком складного згинання з розтяганням (стисканням), при якому брус розтягується силами, паралельними осі бруса, так що рівнодійна їх не збігається з віссю бруса (рис. 1.1), а проходить крізь точку р, що називається полюсом сили.

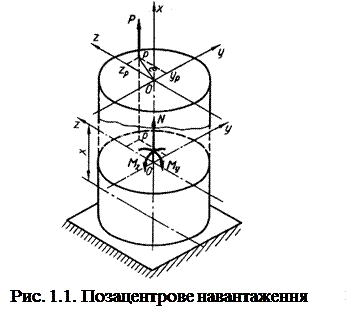
Нехай на брус довільного перерізу діє одна сила Р,яка паралельна осі бруса й перетинає довільний поперечний переріз у точці р (рис. 1.1). Координати цієї точки в системі головних осей перерізу позначимо через у_р та z_р,а відстань цієї точки до осі х, яка називається ексцентриситетом (eccentricity),– через е.У довільному поперечному перерізі при певному навантаженні діють такі внутрішні силові фактори: N = Р; М_у= Рz_р; М_z= Ру_р.

Отже, напруження в довільній точці перерізу складатимуться з напружень осьового розтягання силою N та напружень від чистого згинання моментами М_у та М_z:

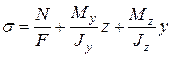. (1.1)

Підставивши сюди замість N, М_у та М_z їхні значення, дістанемо

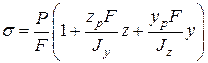. (1.2)

Ця формула набере дещо іншого вигляду, якщо виразити головні моменти інерції через радіуси інерції:

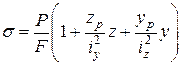. (1.3)

Для визначення небезпечної точки при складному профілі доцільно побудувати нейтральну лінію перерізу. Небезпечною в перерізі буде точка, найвіддаленіша від нейтральної лінії.

Рівняння нейтральної лінії матимемо, прирівнявши до нуля праву частину рівняння (1.3) і позначивши координати точок на нейтральній лінії
через y₀ та z₀:

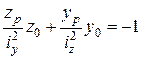. (1.4)

Поклавши в цьому рівнянні по черзі z₀= 0 і у₀ = 0, знайдемо відрізки у_н та z_н, що відсікаються нейтральною лінією на осях у та z (рис. 1.2):

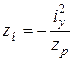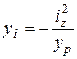; (1.5)

Із залежностей (1.5) випливає, що нейтральна лінія перетинає координатні осі в точках, які належать квадранту, протилежному тому, в якому лежить точка р.

Тепер, провівши паралельно нейтральній лінії дотичні до контуру перерізу, знайдемо найбільш напружені точки А та В у розтягнутій та стиснутій зонах перерізу (рис. 1.2).

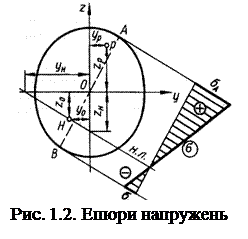
Напруження в цих точках та умови міцності мають вигляд

;

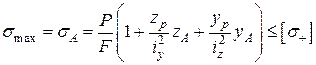(1.6)

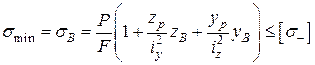Тут z_А, у_А та – z_B, – у_B–– координати точок А та В відповідно. Епюру напружень σ наведено на рис. 1.2. Для прямокутного перерізу умову міцності зручніше записати в такому вигляді:

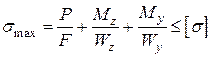. (1.7)

Формули (1.6) та (1.7) справедливі й у випадку дії стискальної сили Р, якщо немає небезпеки виникнення поздовжнього згинання.

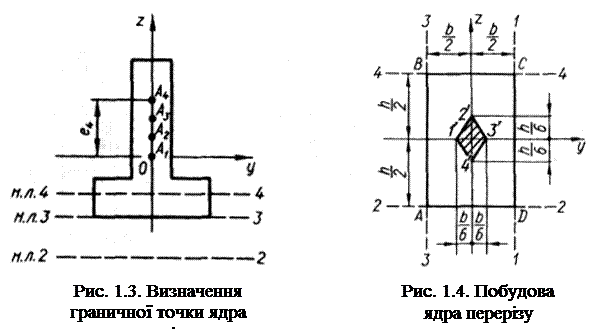
Ядро перерізу (core of a cross-section).Досі ми зображали нейтральну лінію як таку, що проходить крізь переріз. Проте взагалі вона може проходити й поза перерізом. Дійсно, якщо сила Р прикладена в центрі ваги, то нейтральна лінія проходить у нескінченності, оскільки напруження в цьому разі розподілені рівномірно.

Із збільшенням ексцентриситету е (рис. 1.3) нейтральна лінія наближатиметься до перерізу і при деякому положенні сили Р (на рис. 1.3, наприклад, при положенні А₃) вперше торкнеться контуру перерізу. При дальшому збільшенні ексцентриситету нейтральна лінія перетинає переріз, причому нормальні напруження в перерізі будуть обох знаків: по один бік від нейтральної лінії — розтягальними, по інший — стискальними.

Можна визначити зону таких віддалень сили Р від осі, при яких нормальні напруження по всьому поперечному перерізу будуть одного знака. Така зона називається ядром перерізу. Це важливо для брусів з матеріалів, що погано чинять опір розтяганню (наприклад, для цегляної кладки, для бетону та сірого чавуну).

Отже, ядром перерізу називають зону навколо центра ваги поперечного перерізу, яка має таку властивість: якщо позацентрово прикладене навантаження розміщене в зоні ядра, то нормальні напруження в усіх точках поперечного перерізу мають один знак.

Для побудови ядра перерізу будемо задаватися різними положеннями нейтральної лінії, дотичними до контуру перерізу, й обчислювати координати відповідних точок прикладання сили Р за такими формулами, що випливають з виразу (1.5):

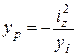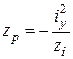; . (1.8)

Обчислені координати визначають точки, що лежать на межі ядра перерізу.

Аби полегшити побудову ядра перерізу, використаємо таку властивість нейтральної лінії: при повороті нейтральної лінії навколо деякої фіксованої точки А контуру перерізу точка прикладання сили переміщується вздовж деякої прямої. Щоб обґрунтувати цю властивість, досить підставити в рівняння (1.4) координати точки А(у_ОА , z_ОА), що лежить на нейтральній лінії. Матимемо

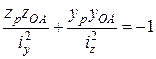. (1.9)

Дійсно, рівняння (1.9) при z_ОА = const є рівнянням прямої лінії відносно координат точок прикладання сили Р – (у_р, z_р).

Отже, для побудови ядра перерізу будь-якої фігури треба провести кілька положень нейтральної лінії, що збігаються зі сторонами перерізу, а також дотикаються до точок, які стирчать.

Побудуємо, наприклад, ядро перерізу для прямокутника АВСВ (рис. 1.4). Сумістимо спочатку нейтральну лінію зі стороною СD (положення 1 – 1). Очевидно, в цьому разі

; .

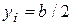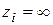Тоді із виразів (1.8)

; .

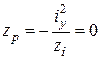Тут ураховано, що

; .

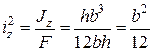Отже, координати точки 1' ядра перерізу визначені.

Сумістимо тепер нейтральну лінію зі стороною АD (положення 2–2). Маємо

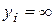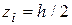Тоді координати точки 2' ядра

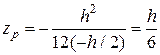Аналогічно визначаються координати точок 3′ та 4', що відповідають положенням 3 – 3 та 4 – 4 нейтральної лінії.

Оскільки при переході нейтральної лінії з одного боку па інший вона повертається навколо кутової точки перерізу, то точка прикладання сили переміщується по прямій, утворюючи контур ядра. Отже, ядро перерізу буде ромбом з діагоналями, які дорівнюють одній третині відповідної сторони перерізу.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
ПОРЯДОК ТА ОСНОВНІ ВИМОГИ ДО ВИКОНАННЯ РОБОТИ	\|	Розв’язування

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.