
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Приклад виконання задачі 9
Зобразити розрахункову схему в аксонометрії. Побудувати окремо епюри згинальних і крутних моментів та визначити діаметри ділянок стержня за третьою теорією міцності, якщо .
На рисунках 1.22 – 1.23 зображена в аксонометрії вісь ламаного стержня круглого поперечного перерізу, розташованого в горизонтальній площині. На стержень діє вертикальне навантаження .
Задача 9. Розрахунок плоскої рами з просторовим навантаженням
Завдання до розрахунково-графічної роботи
Дані взяти з таблиці 1.4.
Таблиця 1.4
| № | Р, кН | q, 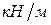
| a, м | b, м | c, м |
| 0,5 | 1,2 | ||||
| 1,2 | 0,5 | ||||
| 1,2 | 0,5 | ||||
| 0,8 | 0,6 | ||||
| 0,5 | 0,8 | ||||
| 0,5 | |||||
| 0,5 | 0,8 | ||||
| 0,6 | 1,2 | ||||
| 0,4 | 0,8 | ||||
Для просторової рами, що навантажена згідно схеми (рис. 1.24) побудувати епюри внутрішніх зусиль та визначити необхідні діаметри поперечних перерізів ділянок за третьою теорією міцності.
Дано:
P = 8 кН; q = 6 кН/м;
a = 1 м; b = 0,6 м; c = 1,2 м;
 = 160 МПа.
= 160 МПа.
Знайти:
dі - ?
1. Будуємо епюри внутрішніх зусиль
Перерізи вибираємо таким чином, щоб розглядати консольну частину рами так як показано на рис. 1.25. Для кожного перерізу вказуємо локальну систему координат таким чином, щоб вісь х співпадала з віссю ділянки та була направлена до частини стержня, що розглядається. Вісь у направляємо вертикально, вісь z утворює праву систему координат. Таким чином, моменти зовнішніх сил відносно осі х будуть крутними моментами, відносно осі у – згинальними моментами в горизонтальній площині, відносно осі z – в вертикальній площині.
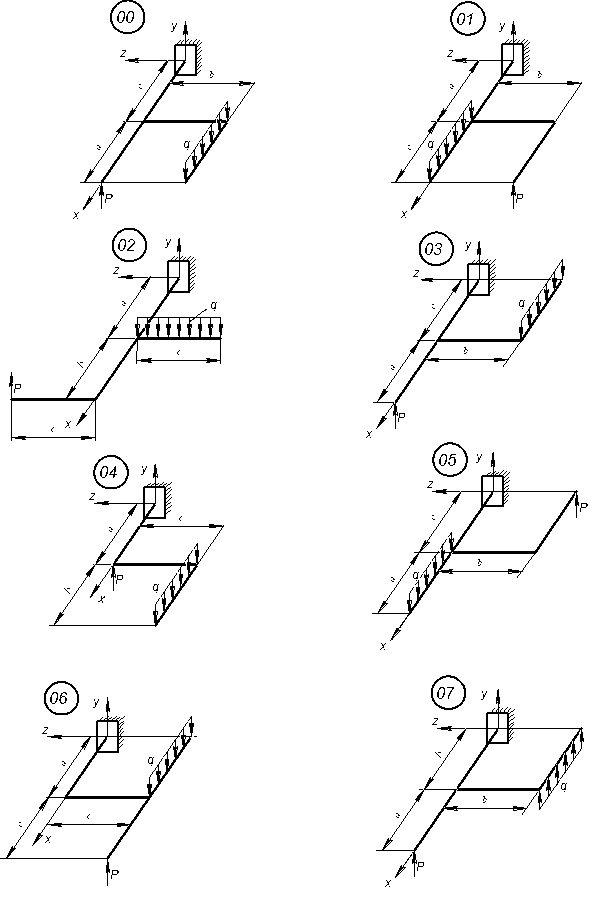
Рис. 1.22. Схеми до виконання задачі 9
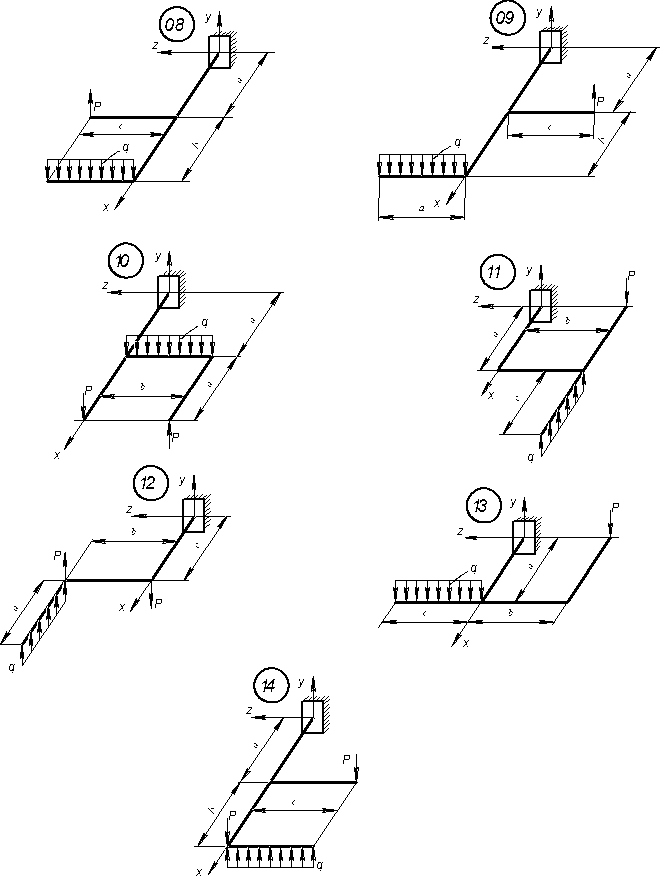
Рис. 1.23. Схеми до виконання задачі 9
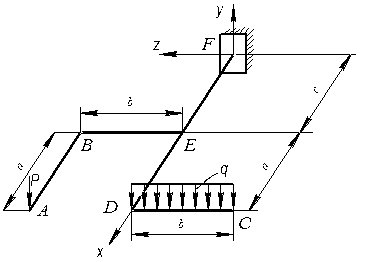
Рис. 1.24. Схема до прикладу задачі 9
Розв’язування
Оскільки навантаження на раму вертикальне, то поперечні сили і згинаючі моменти (епюри) будуть лежати в вертикальній площині xoy.
Поздовжні сили при такому навантаженні в рамі не будуть виникати.
Запишемо для кожної ділянки рівняння поперечних сил, згинаючих та крутних моментів.
Ділянка АВ:
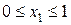 м
м
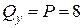 (кН),
(кН),
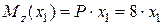 ,
,
при 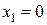 (м)
(м) 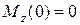 (кН×м),
(кН×м),
при 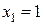 (м)
(м) 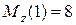 (кН×м).
(кН×м).
Ділянка ВE:
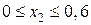 м
м
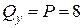 (кН),
(кН),
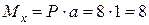 (кН×м),
(кН×м),
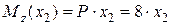 ,
,
при  (м)
(м) 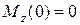 (кН×м),
(кН×м),
при  (м)
(м) 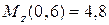 (кН×м).
(кН×м).
Ділянка CD:
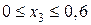 м
м
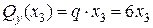 (кН),
(кН),
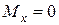 (кН×м),
(кН×м),
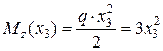 ,
,
при 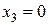 (м)
(м) 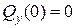 (кН),
(кН),
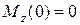 (кН×м),
(кН×м),
при 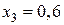 (м)
(м) 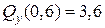 (кН),
(кН),
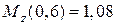 (кН×м).
(кН×м).
Ділянка DE:
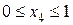 м
м
 (кН),
(кН),
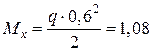 (кН×м),
(кН×м),
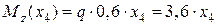 ,
,
при 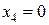 (м)
(м) 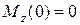 (кН×м),
(кН×м),
при 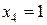 (м)
(м) 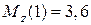 (кН×м).
(кН×м).
Ділянка DE:
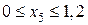 м
м
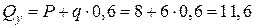 (кН),
(кН),
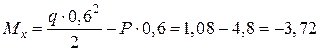 (кН×м),
(кН×м),
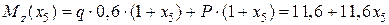 ,
,
при 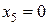 (м)
(м)  (кН×м),
(кН×м),
при 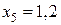 (м)
(м) 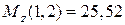 (кН×м).
(кН×м).
Для всіх ділянок 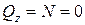 ,
, 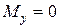 ,
, 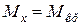 ,
, 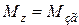 .
.
За отриманими значеннями будуємо епюри в аксонометрії (рис. 1.26).
Епюри згинаючих моментів відкладаємо на розтягнутих волокнах. Розташування епюр крутних моментів особливого значення не має. Додатні значення поперечної сили відкладені над віссю.
2. Розрахунок на міцність
Впливом поперечних сил нехтуємо.
За третьою теорією міцності (найбільших дотичних напружень)
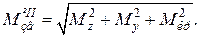
Визначаємо максимальні значення приведених моментів в відповідних точках кожної ділянки
АВ: т. В: 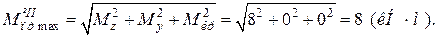
ВЕ: т. Е. 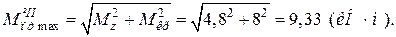
CD: т. D: 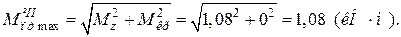
DE: т. E: 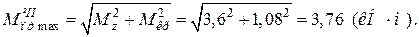
EF: т. F: 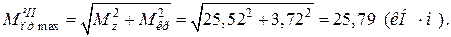
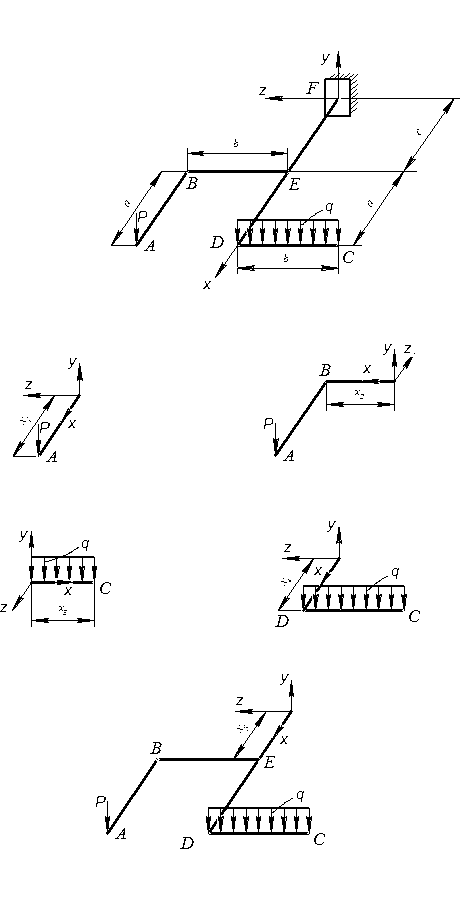
Рис. 1.25. Характерні перерізи на розрахункових ділянках

Рис. 1.26. Епюри внутрішніх зусиль
Розраховуємо мінімальні діаметри ділянок вала за умовою міцності при згині з крученням.
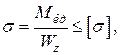
де 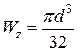 - осьовий момент опору круга, звідки
- осьовий момент опору круга, звідки
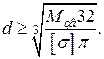
Ділянка АВ:
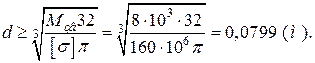
ВЕ: 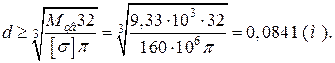
CD: 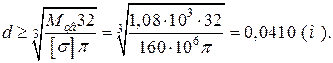
DE: 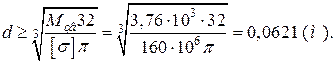
EF: 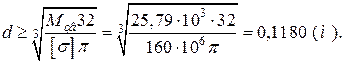
Округлюємо отримані значення до стандартних (Додаток К, ряд Rа 40) та остаточно приймаємо  = 80 мм,
= 80 мм, 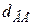 = 85 мм,
= 85 мм, 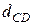 = 42 мм,
= 42 мм, 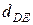 = 63 мм,
= 63 мм, 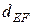 = 120 мм.
= 120 мм.
Відповідь:  = 80 мм,
= 80 мм, 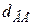 = 85 мм,
= 85 мм, 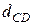 = 42 мм,
= 42 мм, 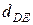 = 63 мм,
= 63 мм, 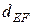 = = 120 мм.
= = 120 мм.
Питання до захисту розрахунково-графічної роботи (задачі 8, 9)
1. Записати умову міцності при згині з крученням та пояснити її.
2. Що таке приведений момент та як він визначається за третьою та четвертою теоріями міцності.
3. Визначити максимальне еквівалентне напруження у вказаному перерізі вала (рами).
4. В яких елементах конструкцій реалізуються деформації згину з крученням – навести приклади.
5. Побудувати епюри розподілу нормальних та дотичних напружень в вказаному перерізі вала.
6. За якою залежністю визначається необхідний діаметр вала (рами) при згині з крученням.
7. За яким алгоритмом виконують розрахунки вала при згині з крученням.
8. Які епюри внутрішніх зусиль вказують на згин з крученням. Які епюри не використовуються в розрахунку і чому?
9. Чому для вала будують епюри в двох розрахункових площинах – вертикальні та горизонтальні? Чи має значення саме такий вибір площин?
Читайте також:
- III. Виконання бюджету
- III. Вимоги безпеки під час виконання роботи
- III. Вимоги безпеки під час виконання роботи
- V. Виконання вправ на застосування узагальнювальних правил.
- Абсолютні синоніми (наприклад, власне мовні й запозичені) в одному тексті ділового стилю вживати не рекомендується.
- Алгоритм однофакторного дисперсійного аналізу за Фішером. Приклад
- Алгоритм розв’язання задачі
- Алгоритм розв’язання розподільної задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
| <== попередня сторінка | | | наступна сторінка ==> |
| Приклад виконання задачі 8 | | | Узагальнені сили і переміщення |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |