• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Узагальнені сили і переміщення

Короткі теоретичні відомості

ЕНЕРГЕТИЧНІ МЕТОДИ ВИЗНАЧЕННЯ ПЕРЕМІЩЕНЬ

Однією з найважливіших задач опору матеріалів є оцінка жорсткості конструкції, тобто ступеня її викривлення під дією навантаження, зміщен­ня зв'язків, зміни температури. Для розв'язання цієї задачі треба визначити переміщення (лінійні та кутові) довільно навантаженої пружної системи (балки, рами, криволінійного стрижня, ферми тощо). Така сама задача постає при розрахунку конструкцій на динамічні навантаження і при виявленні статичної невизначуваності системи. В останньому випадку, як уже зазначалося, складають рівняння спільності деформацій, які містять у собі переміщення певних перерізів.

Розглядатимемо загальний метод визначення переміщень у стрижневих системах, який ґрунтується на двох фундаментальних принципах механіки: почат­ку можливих переміщень і законі зберігання енергії.

Як відомо з теоретичної механіки, робота постійної сили Р на переміщенні Δ за її напрямом дорівнює добутку значення сили на зазначене переміщення:

.

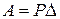У задачах опору матеріалів і будівельної механіки зовнішні навантаження відзначаються великою різноманітністю і, як правило, становлять групи сил. Вираз для роботи групи постійних сил також можна подати у вигляді добутку двох величин:

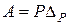, (2.1)

у якому множник Р залежить тільки від сил групи і називається узагальненою силою (generalized force), а Δ_Р залежить від переміщень і називається узагальненим пе­реміщенням (generalized displacement).

Отже, під узагальненою силою будемо розуміти будь-яке навантаження (зосереджені сили, зосереджені моменти, розподілене навантаження), а під узагальненим переміщенням – той вид переміщення, на якому узагальне­на сила здійснює роботу.

Розглянемо деякі приклади узагальнених сил і переміщень.

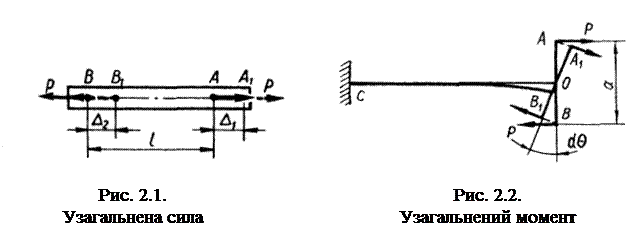
1. На рис. 2.1 зображено узагальнену силу, яка складається з двох одна­кових за модулем протилежних сил Р,прикладених у точках А та В і напрямлених по одній прямій. Припустимо, що точки прикладення сил пе­ремістились у напрямі ВА на відрізки Δ₁ і Δ₂. Очевидно, робота системи постійних сил на цих переміщеннях

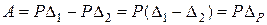, (2.2)

де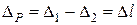– зміна відстані l між точками прикладення сил.

Отже, в цьому прикладі Р – узагальнена сила, а зміна Δl довжини відрізка АВ –узагальнене переміщення.

2. Нехай група сил складається з пари сил, момент якої М = Ра (рис. 2.2). Припустимо, що елемент АВ повернувся на кут dθ. Шляхи, пройдені силами пари в напрямі їхньої дії,

; .

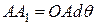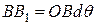Сумарна робота обох сил

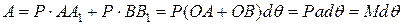. (2.3)

Отже, якщо узагальненою силою є момент М пари, то узагальненим пе­реміщенням буде кут повороту dθ у площині дії пари.

Легко також довести, що при дії на елементи АВ і СD (рис. 2.3) двох однакових за модулем і протилежно напрямлених пар з моментом М узагальненою силою є момент пари М, а узагальненим переміщенням – зміна кута φ між елементами АВ і СD. Інакше

.

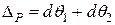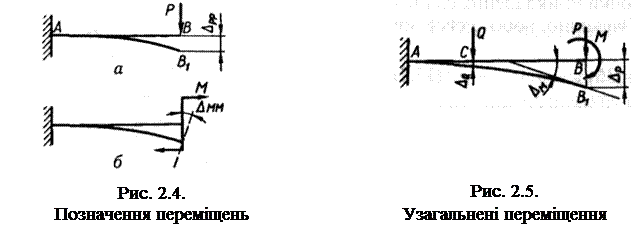
Умовимося надалі узагальнені переміщення (як лінійні, так і кутові) якого-небудь перерізу стрижня позначати літерою Δ або δ з двома індекса­ми. Перший індекс відображує точку і напрям переміщення, другий – указує причину цього переміщення. Наприклад, Δ_РР означає переміщення точки прикладення сили Р у напрямі її дії, спричинене цією самою силою (рис. 2.4, а). На рис. 2.4, б зобра­жено консоль, навантажену на вільному кінці зосе­редженим моментом. Очевидно, кут повороту пе­рерізу, де прикладений момент, слід позначити Δ_ММ. Тут перший індекс означає переміщення в напрямі моменту М.

Для позначення повного переміщення точки, спричиненого кількома зусиллями, при Δ збері­гається тільки перший індекс. Так, повний прогин і кут повороту перерізу В балки, зображеної на рис. 2.5, слід позначити відповідно через Δ_Р і Δ_М,прогин перерізу С – через Δ_Q.

Розглядаючи досить жорсткі лінійно деформівні конструкції (тобто системи, деформації яких відповідають закону Гука), можна на підставі принципу незалежності дії сил визначати повні переміщення точок як суму переміщень, спричи­нених окремими навантаженнями.

Для зображеної на рис. 2.5 балки прогин і кут повороту перерізу В можна записати у виг­ляді

;

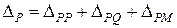(2.4)

.

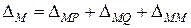де Δ_РР – переміщення точки В у напрямі сили Р від сили Р; Δ_РQ – те саме від сили Q; Δ_РМ – те саме від моменту М; Δ_МР – переміщення перерізу В у напрямі пари М (кут повороту) від сили Р; Δ_МQ – те саме від си­ли; Δ_MМ – те саме від пари М.

Переміщення, спричинене одиничною силою (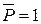) або одиничною парою (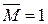), будемо позначати літерою δ і називати питомим. При цьому умовимося вважати одиничні сили чи пари, які спричинюють переміщення δ, безрозмірними.

Якщо одинична сила 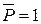спричинила переміщення δ_Р, то, згідно з принципом незалежності дії сил, повне переміщення, спричинене силою Р,

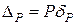. (2.5)

З виразу (2.5) легко визначити одиницю питомого переміщення:

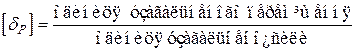. (2.6)

Зазначимо, що навантаження, яке діє на конструкцію, як правило, по­значають літерами Р, М, Х, …з числовими індексами (наприклад, Х₁, Х₂, …). У цьому разі літерні індекси при Δ або δ заміняють відповідними числовими, тобто замість пишуть Δ₁, (Δ ₂, δ₁₂, …).

На рис. 2.6 зображено позначення переміщень вільного кінця рами від дії різних сил (Р, Х₁, Х₂, Х₃). Повні переміщення перерізу С у горизонтальному і вертикальному напрямах (тобто в напрямах дії сил Х₁ і Х₂), а також кут повороту (переміщення в напрямі дії Х₃) відповідно можна подати у вигляді

;

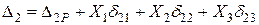; (2.7)

.

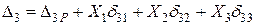Тут

; ; ; .

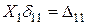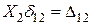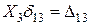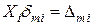Для оцінки одиниці переміщення 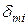множимо останнє рівняння на Х_т.

Тоді

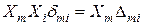
виражатиметься в одиницях роботи (Дж). Звідси переміщення

.

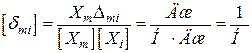Читайте також:

1. L2.T4/1.Переміщення твердих речовин по території хімічного підприємства.
2. L3.T4/2. Засоби переміщення рідин.
3. Б- не збуджена ділянка мембрани , на яку діють електричні струми збудженої ділянки. Стрілками показано напрям струмів, кружечками – дійсне переміщення іонів.
4. Векторні характеристикимеханічного руху– переміщення, шлях, швидкіст та прискорення
5. Визначення напрямку переміщення блоків скидів
6. Візок для піднімання та переміщення котлів
7. Граничні норми підіймання і переміщення важких речей неповнолітніми
8. Граничні норми підіймання та переміщення вантажів непованолітніми під час короткочасної та тривалої роботи
9. Загально існуючі схеми переміщення вантажів
10. Злочини проти встановленого порядку переміщення предметів через митний кордон України
11. Зміна розмірів і переміщення малюнка
12. Колективний та трудовий договори, порядок укладання. Переведення та переміщення в галузі охорони здоров'я.

Переглядів: 2805