• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Загальна формула для визначення переміщень. Метод Мора

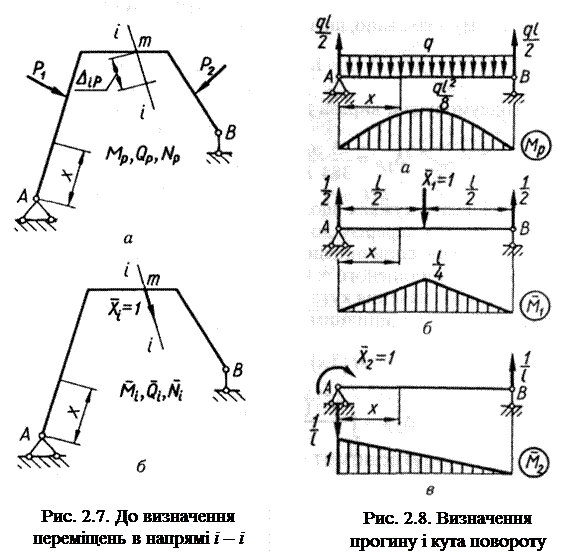
Розглянемо довільну плоску стрижневу систему (балку, раму, ферму тощо), навантажену заданими силами Р (рис. 2.7, а). Зусилля в до­вільному перерізі системи позначимо через М_р, Q_p, N_р.Нехай треба визна­чити переміщення (узагальнене) будь-якої точки системи в напрямі і – і.

Введемо допоміжний стан (рис. 2.7, б), що є заданою системою, навантаженою лише однією одиничною силою (узагальненою) 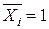, прикладеною в тій самій точці т і в напрямі шуканого переміщення Δ_іР. Зусилля в довільному перерізі допоміжного стану, спричинені дією одинич­ної сили 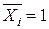, позначимо через , , .

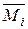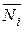У загальному випадку дії сил формула для переміщення містить шість доданків:

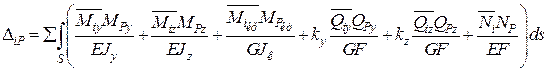. (2.8)

Індекси у, z у формулі (2.8) позначають головні осі, індекс «кр» – крутний момент. Зазначимо, що наведену формулу можна застосувати і для кривих стрижнів малої кривини.

Формулу (2.8) вперше було виведено Мором. Визначення переміщень за цією формулою часто називають методом Мора (dummy-load method, Maxweel-Mohr method, unit-load method). Зазна­чимо, що метод Мора – це найзагальніший метод визначення переміщень стрижневих систем. Його значення особливо велике при розрахунку ста­тично невизначуваних систем.

Здебільшого при визначенні переміщень у балках, рамах та арках мож­на знехтувати впливом поздовжніх деформацій і деформацій зсуву, вра­ховуючи лише переміщення, спричинені згинанням і крученням. Тоді фор­мула (2.8) для плоскої системи набирає вигляду

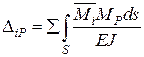. (2.9)

При просторовому навантажуванні, згідно з формулою (2.8),

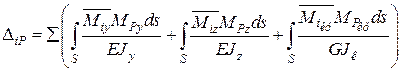. (2.10)

При визначенні переміщень вузлів шарнір­них ферм, що складаються з прямих стрижнів, у формулі Мора зберігається тільки один дода­нок:

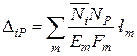. (2.11)

Ця формула має назву формули Максвелла.

Можна запропонувати таку послідовність визначення переміщень за методом Мора:

1. Будують допоміжну систему, яку наванта­жують одиничним навантаженням у точці, де треба визначити переміщення. Визначаючи лінійні переміщення, у заданому напрямі при­кладають одиничну силу, визначаючи кутові переміщення, – одиничний момент.

2. Для кожної ділянки системи записують вирази силових факторів у довільному перерізі заданої (М_р, N_р, Q_p)і допоміжної (,,)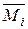
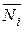систем.

2. Обчислюють інтеграли Мора (по ділян­ках у межах всієї системи). Як вже зазначало­ся, при розрахунку плоских балок, рам і арок виходять з формули (2.9), просторових систем – (2.10), ферм – (2.11).

4. Якщо обчислене переміщення додатне, то це означає, що його напрям збігається з вибра­ним напрямом одиничної сили. Від'ємний знак свідчить про те, що дійсний напрям шуканого переміщення протилежний напряму одиничної сили.

Розглянемо приклади застосування методу Мора для визначення переміщень у різних стрижневих системах.

Припустимо, що треба визначити прогин посередині прогону та кут повороту на опорі шарнірно обпертої балки (EJ = const), навантаженої рівномірно розподі­леним навантаженням інтенсивністю q (рис. 2.8, а), а також дослідити вплив поперечних сил на максимальний прогин.

1. Для визначення прогину посередині прогону прикладаємо в цьому місці допоміжної балки (рис. 2.8, б) одиничну зосереджену силу. В довільному перерізі першої ділянки балки (0 ≤ х ≤ l/2)

; .

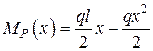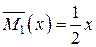Ураховуючи симетрію, дістанемо

.

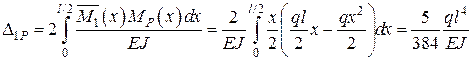Врахуємо вплив дотичних напружень на шуканий прогин, припускаю­чи, що балка має прямокутний переріз. Очевидно, при 0 ≤ х ≤ l/2

; .

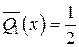На підставі формули (2.8) прогин, спричинений дією поперечних сил,

.

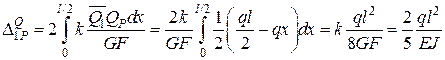При цьому враховано, що коефіцієнт форми для прямокутного перерізу

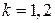, а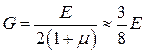

Підсумовуючи вирази для переміщень, знаходимо, що

.

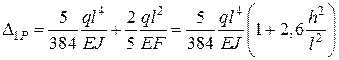Другий член у дужках, що відображує вплив поперечної сили, при відно­шенні висоти перерізу до довжини прогону h/l = 1/10 дорівнює 0,026. Отже, прогин, спричинений поперечною силою, становить менше ніж 3% прогину, спричиненого згинальними моментами.

2. Для визначення кута повороту опорного перерізу допоміжну балку навантажуємо одиничним моментом (рис. 2.8, в). При 0 ≤ х ≤ l/2 маємо

; ;

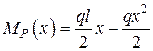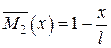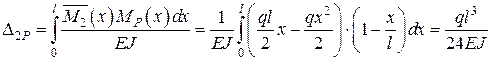. (2.12)

Додатний знак свідчить про те, що напрям повороту збігається з на­прямом одиничного моменту.

Визначимо вертикальне переміщення вузла В шарнірно-стрижневої сис­теми (рис. 2.9, а), яка складається з двох однакових стрижнів АВ і ВС пос­тійного поперечного перерізу. Допоміжну систему зображено на рис. 2.9, б.

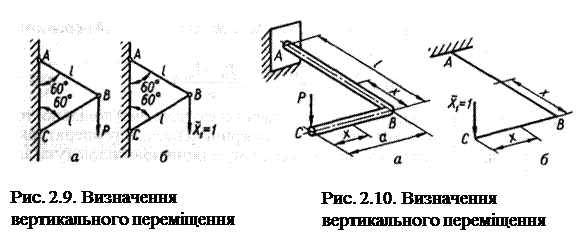
Розглядаючи рівновагу вирізаного вузла В, знаходимо зусилля в стриж­нях для обох станів:

Стрижень N_P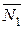
AB Р 1

ВС –P –1

З формули (2.11) маємо

(2.13)

Приклад. Розміщена в горизонтальній площині рама АВС (рис. 2.10, а) скла­дається з двох стрижнів однакового круглого поперечного перерізу. Визначимо верти­кальне переміщення точки С. Допоміжну систему зображено на рис. 2.10, б.

Переміщення Δ­­_1P можна визначити з формули (2.8). Для довільних перерізів двох ділянок маємо:

для І ділянки (0 ≤ х ≤ l/2)

;; ; ;

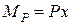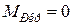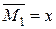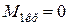для ІІ ділянки (0 ≤ х ≤ l)

;; ; ;

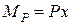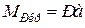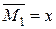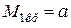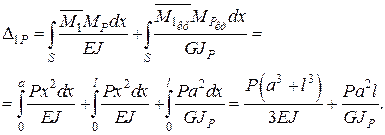(2.14)

Читайте також:

1. D) методу мозкового штурму.
2. H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
3. I визначення впливу окремих факторів
4. I Метод Шеннона-Фано
5. I. Загальна характеристика політичної та правової думки античної Греції.
6. I. Метод рiвних вiдрiзкiв.
7. II. Визначення мети запровадження конкретної ВЕЗ з ураху­ванням її виду.
8. II. Мотивація навчальної діяльності. Визначення теми і мети уроку
9. Ni - загальна кількість періодів, протягом яких діє процентна ставка ri.
10. Ocнoвнi визначення здоров'я
11. VII. Нахождение общего решения методом характеристик
12. А. науковий факт, b. гіпотеза, с. метод

Переглядів: 4339