• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розрахунки на міцність

Аналіз напруженого стану при згині.

Поперечний згин. Дотичні напруження

При поперечному згині бруса в його перерізах, крім згинального моменту діє поперечна сила. У цьому випадку, крім нормальних напружень від згинального моменту, у перерізах виникають також дотичні напруження від поперечної сили. Їх розраховують за формулою Журавського

, (8.25)

де Q_y - поперечна сила в перерізі, b- ширина перерізу в тому місці, де треба обчислити дотичні напруження, S^*_z - абсолютна величина статичного моменту площі відносно осі z тієї частини площі перерізу A^*,

Рисунок 8.10

яка відсікається прямою, паралельною нейтральній осі z, проведеній через точку, в якій визначається дотичне напруження, Iz - момент інерції перерізу відносно осі z

(рисунок 8.10, а).

Оскільки для перерізу Q_y і I_z величини сталі, то закон розподілу дотичних напружень по висоті перерізу визначається відношенням . Наприклад, для прямокутного перерізу

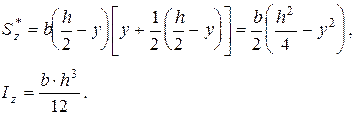
Підставивши значення S^*_z і I_z в (8.25), отримаємо

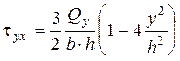. (8.26)

Отже, по висоті прямокутного перерізу дотичні напруження змінюються за параболічним законом. Найбільшого значення дотичні напруження досягають в точках, розташованих на нейтральній лінії при y=0 (рисунок 8.10).

Як видно із рисунка 8.9 і рисунка 8.10 в точках, які лежать на верхній і нижній границях поперечного перерізу, мають місце тільки нормальні напруження і в цих точках вони мають найбільше значення. Таким чином для цих точок умову міцності можна записати у вигляді

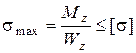. (8.27)

Якщо матеріал крихкий і по різному чинить опір розтяганню і стисканню, то балки із такого матеріалу мають несиметричний по відношенню до нейтральної лінії переріз (рис. 8.8, г). Такі балки розміщують так, щоб більші за абсолютною величиною напруження були стискувальні, а менші - розтягувальні (рисунок 8.9, д). Умови міцності для таких випадків приймають вигляд

(8.28)

де [s]_р - допустиме напруження при розтяганні, а [s]_с - допустиме напруження при стисканні.

Рисунок 8.11

Таким чином для балок із пластичних матеріалів, які однаково працюють на розтяг і стиск, доцільно вибирати перерізи, симетричні відносно їх нейтральних осей. При цьому забезпечується однаковий запас міцності по стиснутих і розтягнутих волокнах Якщо крім умови міцності виходити ще із вимоги мінімальної маси балки, то найбільш раціональним буде переріз, який при заданій величині моменту опору Wz має найменшу площу перерізу А,

або при заданій площі А - найбільший момент опору W_z . Порівнюючи з цих позицій, наприклад, прямокутний переріз з двотавровим, неважко переконатись в перевазі останнього.

У балки прямокутного перерізу матеріал в області нейтральної лінії повністю не використовується, оскільки знаходиться в зоні з малими напруженнями. У двотаврової балки більша частина матеріалу розміщена в найбільш напруженій зоні. Тому при однаковій міцності двотаврова балка в 2...3 рази легша прямокутної. В точках перерізу, розміщених на нейтральній осі, діють тільки дотичні напруження (рисунках 8.9 і 8.10), тому умова міцності для цих точок буде така:

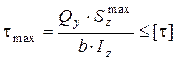. (8.29)

В решти точок перерізу при поперечному згині має місце плоский напружений стан, тобто одночасно діють дотичні і нормальні напруження (рисунок 8.11). Умова міцності записується у вигляді

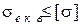. (8.30)

Головні напруження в цих точках визначаються за формулами

(8.31)

Еквівалентне напруження s_екв вибирається в залежності від прийнятої теорії міцності.

Для пластичних матеріалів - за третьою теорією міцності.

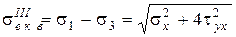. (8.32)

Для крихких матеріалів за теорією Мора

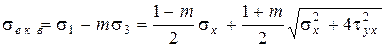, (8.33)

де .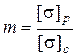

Більшість розрахунків на міцність при згині роблять за формулою (8.27). Для цього необхідно побудувати епюру згинальних моментів M_z і по ній визначити небезпечний переріз, тобто той переріз, в якому M_z має найбільше значення.

Можливі випадки, коли при великих поперечних силах в перерізах балки діють незначні згинальні моменти (короткі балки). В цьому випадку підбирають переріз по (8.27) і обов’язково перевіряють чи виконується умова міцності (8.29) для точок, які лежать на нейтральній лінії. Перерізи, в яких діють найбільша поперечна сила і найбільший згинальний момент можуть збігатися.

В балках з тонкостінним перерізом небезпечною може бути точка перерізу, розміщена в місці переходу стінки в полку (рисунок 8.9, г). Тут має місце плоский напружений стан, тобто s_х¹0, t_ух¹0.

Для перевірки міцності таких балок необхідно:

1. Визначити переріз, в якому діє найбільший згинальний

момент і за (8.27) підібрати переріз.

2. Знайти переріз балки, в якому одночасно M_z і Q_y мають найбільші значення. Такий вибір не завжди однозначний, тому бувають випадки, коли таких перерізів більше одного.

3. Перевірити за формулами (8.32) або (8.33), залежно від матеріалу балки, чи виконуються ці умови міцності для небезпечної точки. Якщо умови міцності (8.32) або (8.33) не виконуються, то збільшуютьплощу перерізу, або вибирають по сортаменту більший номер профілю.

Розглянемо наступний приклад.

Підібрати двотавровий переріз для балки, показаної на рисунку 8.12, а, якщо а=0,5 м, кН/м, [s]=160 МПа.

Епюри поперечних сил і згинальних моментів показані на рисунках 8.12,б і 8.12,в.

За формулою (8.27) знаходимо

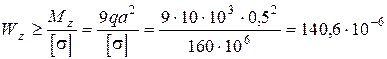м³=140,6 см³

По сортаменту підбираємо двотавр № 18,а (рисунок 8.12, г), для якого см³, 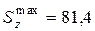см³, І_z=1290 см⁴, h=180 мм, b=90 мм, d=5,1 мм, t=8,1 мм.

Перевіримо, чи виконується умова міцності для точки, яка знаходиться в перерізі з найбільшою поперечною силою

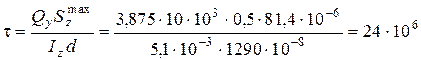Н/м²=

=24 МПа < 0,5[s]=80 МПа

Таким чином, міцність за дотичними напруженнями в точці “4” забезпечена.

Перевіримо міцність в точці “2”, для перерізу, в якому діють найбільші поперечна сила і згинальний момент. Таким перерізом буде переріз D.

Рисунок 8.12

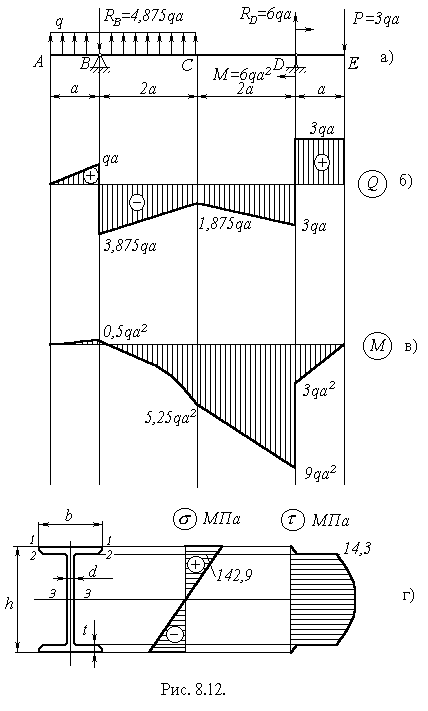
Визначимо нормальне напруження в точці “2”

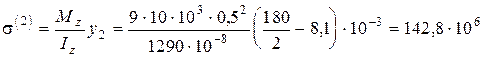Н/м²=148 МПа

Дотичне напруження в точці “2”

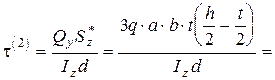
Н/м²=14,3 МПа

Визначимо нормальне напруження в точці “2”

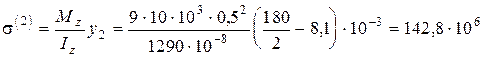Н/м²=148 МПа

Визначаємо головні напруження

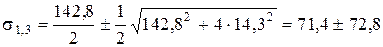
s₁=144,2 МПа, s₃=-1,4 МПа.

Еквівалентне напруження за третьою теорією міцності

МПа < [s]=160мпа.

Умова міцності для точки “2” також виконується.

Читайте також:

1. А. Розрахунки з використанням дистанційного банкінгу.
2. Актуарні розрахунки
3. АКТУАРНІ РОЗРАХУНКИ
4. Безготівкові розрахунки
5. Безготівкові розрахунки із застосуванням платіжних доручень, платіжних вимог-доручень, платіжних вимог
6. Безготівкові розрахунки фізичних осіб розрахунковими чеками
7. Безготівкові та готівкові розрахунки
8. В. Розрахунки через Інтернет
9. Взаємні розрахунки між бюджетами.
10. Взаєморозрахунки з контрагентами та податковий облік: основні принципи
11. Вплив фьючерсних бірж на ціноутворення та фінансові розрахунки
12. Гідроенергетичні розрахунки

Переглядів: 3444